Проблемы распараллеливания метода частиц в ячейках для задачи взаимодействия электронного пучка с плазмой

Содержание
Проблемы эффективного распараллеливания для большого числа процессоров
Моделирование динамики плазмы методом частиц в ячейках
Проведение больших численных расчетов на суперЭВМ
О реализации метода частиц на GPU

Проблемы эффективного распараллеливания для большого числа процессоров
Решение уравнения Пуассона
Параллельная прогонка
Метод частиц в ячейках

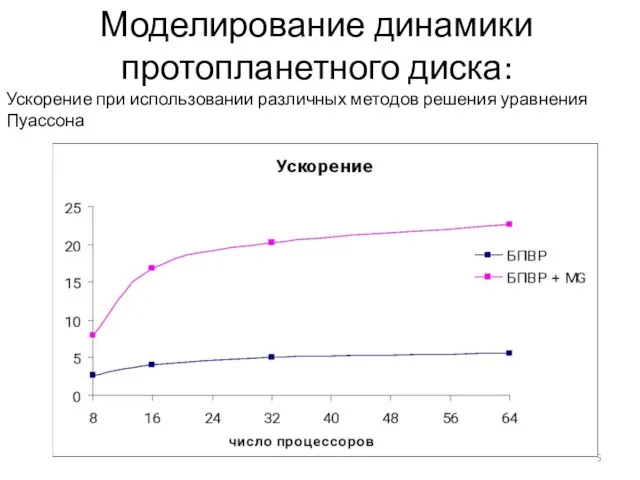
Многосеточный метод:
Ускорение параллельной программы
0-я гармоника вычисляется с помощью
многосеточного метода на отдельном процессоре
Остальные гармоники: метод БПВР
Сетка:
511×512×511
100 млн. частиц
Моделирование динамики
протопланетного диска:
Ускорение при использовании различных методов решения уравнения Пуассона

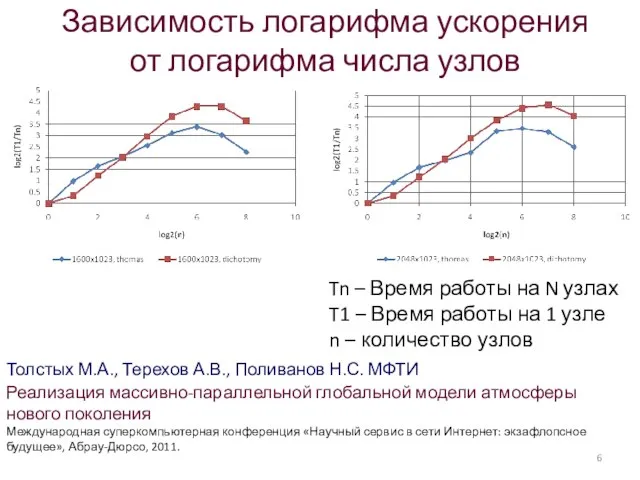
Зависимость логарифма ускорения от логарифма числа узлов
Tn – Время работы на N узлах
T1 – Время работы на 1 узле
n – количество узлов
Реализация массивно-параллельной глобальной модели атмосферы нового поколения
Толстых М.А., Терехов А.В., Поливанов Н.С. МФТИ
Международная суперкомпьютерная конференция «Научный сервис в сети Интернет: экзафлопсное
будущее», Абрау-Дюрсо, 2011.

Всероссийская конференция
«Актуальные проблемы вычислительной математики и математического моделирования»
13 - 15 июня 2012 года
Новосибирск, Россия
Председатели программного комитета:
академик Марчук Г.И.
академик Михайленко Б.Г.
Тематика конференции:
Математическое моделирование и Параллельные вычислительные методы

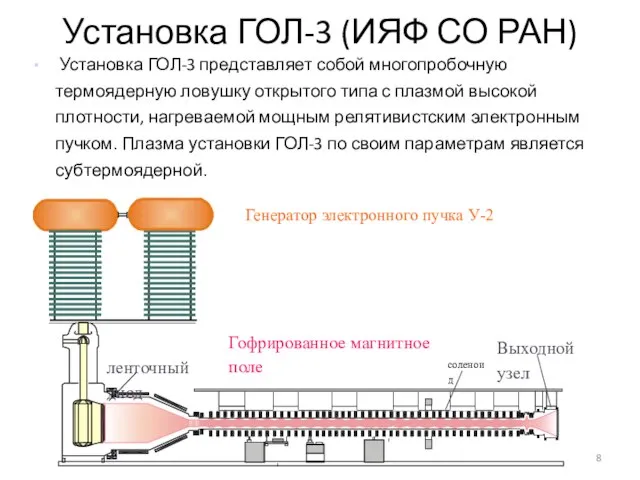
Установка ГОЛ-3 (ИЯФ СО РАН)‏
Установка ГОЛ-3 представляет собой многопробочную термоядерную ловушку открытого типа с плазмой высокой плотности, нагреваемой мощным релятивистским электронным пучком. Плазма установки ГОЛ-3 по своим параметрам является субтермоядерной.
ленточный диод
Генератор электронного пучка У-2
Гофрированное магнитное поле
Выходной узел
соленоид

Эффект аномальной теплопроводности
В экспериментах на установке ГОЛ-3 (ИЯФ СО РАН) вследствие релаксации мощного электронного пучка наблюдается понижение электронной теплопроводности
Коэффициент электронной теплопроводности уменьшается в 102-103 раз по сравнению с классическим значением для плазмы с такой плотностью и температурой
Это позволяет лучше нагревать плазму и дольше удерживать ее в нагретом состоянии вследствие намного меньшего теплового потока на стенки установки

Система уравнений Власова-Максвелла
Плазма описывается системой уравнений Власова-Максвелла:
где - функция распределения частиц сорта (электроны или ионы), - скорость света, - плотность электрического заряда, - плотность электрического тока, - заряд частицы сорта .

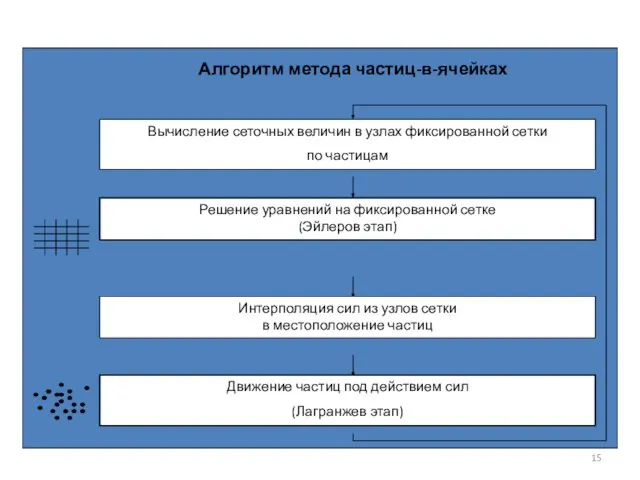
Лагранжев этап

Эйлеров этап
Эйлеров этап:
Схема эйлерова этапа:

Восстановление плотности заряда по частицам
NGP:
PIC:

Схема вычисления токов

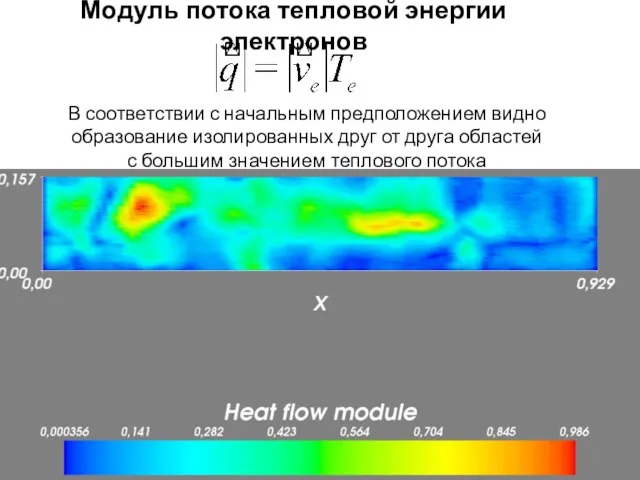
Модуль потока тепловой энергии электронов
В соответствии с начальным предположением видно
образование изолированных друг от друга областей
с большим значением теплового потока

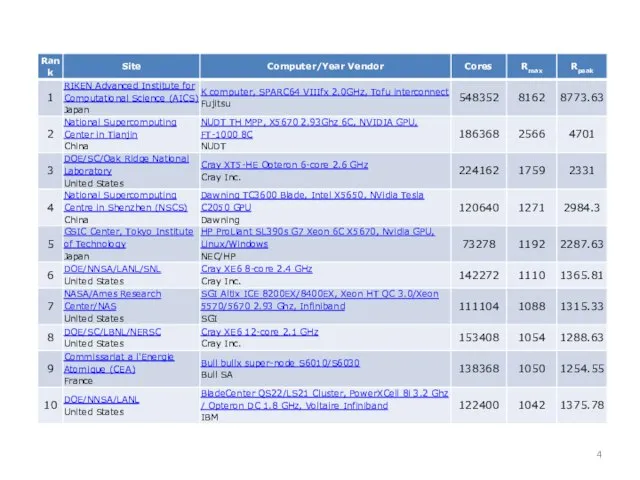
Проведение больших численных расчетов на суперЭВМ
Оценка производительности суперЭВМ
Повышение размерности задачи
Компьютер — это не только процессоры
Требования к системам хранения и передачи данных

Оценка производительности суперЭВМ
Принятая единица — FlOpS (теоретические, или реально достигнутые, напр. LINPACK )
Однако для реальных задач большее значение имеет быстродействие (и объем) оперативной памяти,
а также жесткого диска
Время работы процедуры интегрирования на 1 шаге:
СКИФ-МГУ – 0.422 сек
МВС-100К – 0.896 сек

Значение объема жесткого диска
Пример конкретной задачи
Релаксация мощного релятивистского пучка в высокотемпературной плазме, метод частиц-в-ячейках, сетка 512х64х64, 150 частиц в ячейке
Изучается трехмерная динамика теплопроводности и фурье-образы основных величин (плотности, электрического поля — на данный момент 4 величины)
Одна выдача занимает 160 Мб (архив 20)
Необходимо от 100 до 400 моментов
Требуется выдать все это на диск за ограниченное время работы программы — (один файл, СКИФ МГУ vs МВС-100К: 0.0134 сек. vs 0.0364 cек.)
И не превысить дисковую квоту — возможно, это в большей степени вопрос администрирования — но он существует
А потом еще передать по сети на локальный компьютер для обработки — по этой причине трехмерные выдачи делались пока только на НКС-30Т (ИВМиМГ СО РАН)

Повышение размерности задачи
Существуют планы по поводу вычислений Exascale-масштабе.
Тем не менее, лишь небольшое количество программ сейчас используют 1000 ядер (или больше), т.е. терафлопные мощности.
Опыт проведения крупномасштабных расчетов свидетельствует, что при увеличении размерности на порядок появляются принципиально новые трудности в реализации алгоритма.
Поэтому категорически нельзя сразу переходить от мелких, отладочных задач к крупномасштабным.
А речь идет о повышении размерности на 6 порядков...

Компьютер — это не только процессоры
Результат расчета в задачах физики плазмы (не только в рассмотренной выше) - это прежде всего, трехмерные распределения плотности частиц, токов, распределения электромагнитного поля (сетка 20003).
Для сравнения численного результата с известными физическими закономерностями необходимо вычислить фурье-образ рассматриваемой величины
Если они выдаются в двоичном формате, то размер одной такой выдачи составит 60 Гб. Но это один момент времени, в то время как требуется от 100 до 300 моментов времени с выдачей в течение одного расчета, то есть около 18 Петабайт
Более того, для решения какого-то отдельного вопроса в рамках задачи необходимо несколько (5-10) расчетов, то есть всего получается около 200 Петабайт.

Требования к системам хранения и передачи данных
Объем диска - 200 Петабайт.
Скорость диска - 270 Гбайт/сек (для обработки указанного массива данных в течение часа). Сейчас для SSD-дисков скорость чтения порядка 0.7 Гб/сек.
Скорость сетевого соединения - 11 Гб/сек (для передачи этого массива данных по сети в течение суток), при том, что сейчас время передачи 1 Гб данных по внутренней сети ННЦ СО РАН занимает около получаса, т.е. 0.0005 Гб/сек.
Видно, что недостаток мощности систем хранения и передачи данных между текущим состоянием и перспективными экзафлопс-компьютерами ненамного меньше, чем по вычислительным мощностям (при том, что системам хранения данных традиционно уделяется меньше внимания).

О реализации метода частиц на GPU
Необходимость
Методика
Результаты

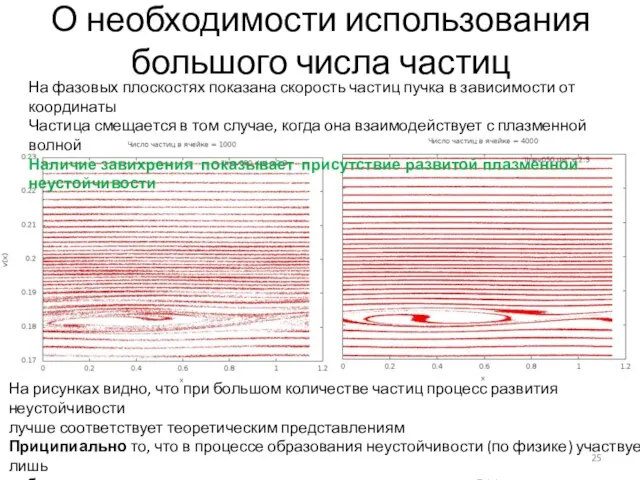
О необходимости использования большого числа частиц
На фазовых плоскостях показана скорость частиц пучка в зависимости от координаты
Частица смещается в том случае, когда она взаимодействует с плазменной волной
Наличие завихрения показывает присутствие развитой плазменной неустойчивости
На рисунках видно, что при большом количестве частиц процесс развития неустойчивости
лучше соответствует теоретическим представлениям
Приципиально то, что в процессе образования неустойчивости (по физике) участвует лишь
небольшая доля частиц пучка, и при числе частиц, меньшем 500,
неустойчивость не возникает

Оценка размера задачи
В настоящее время проведены расчеты взаимодействия релятивистского электронного пучка с плазмой, позволившие в квазиодномерном случае точно рассчитать инкремент двухпотоковой неустойчивости
Получено g = 0.081, точное значение g = 0.077 (К.В.Лотов и др., Физика плазмы, 2009).
Однако для этого пришлось значительно увеличить число модельных частиц а именно до 1000 в одной ячейке.
При этом величина дебаевского радиуса 8.9x10-3 в тех же единицах.
Таким образом длина области в дебаевских радиусах составляет 134.8.
Таким образом, получаем следующую оценку размера сетки: 2156х2156х2156 при 1000 модельных частиц каждого типа в ячейке.
Это означает объем памяти 1.4 Петабайт и вычислительную нагрузку порядка 1.5 PetaFLOP (около 50 операций на каждую частицу)

Моделирование плазменных неустойчивостей требует кинетического подхода и больших вычислительных ресурсов:
Требуется от 1000 частиц в ячейке
Расчетная сетка (минимально) от 1003 узлов
В настоящий момент сетка 512х64х64, 150 частиц в ячейке рассчитывается за 26 часов на 140 ядрах
Скорость счета ~ 129 мегачастиц/час на ядро
1 млрд. частиц рассчитывается за 1 минуту на 500 ядрах (1 временной шаг из … 10000 !!!)

Использование текстур CUDA
Что такое текстура: способ доступа к памяти
Двух- или трехмерный массив с кэшированием, оптимизированным для двумерной адресации
Двумерные координаты текстуры означают:
Номер ячейки, i
Номер частицы в ячейке, j
Атрибуты частицы хранятся в 6 разных текстурах

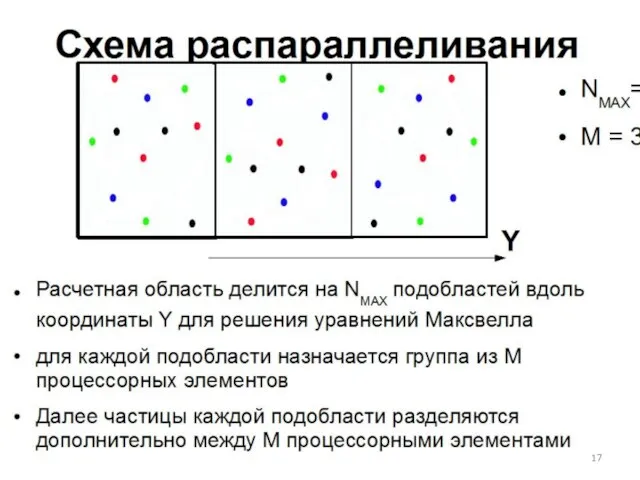
Перспективы достижения экзафлопс-производительности для метода частиц-в-ячейках на GPU
Используемая в настоящий момент одномерная декомпозиция области не может обеспечить достаточную масштабируемость
Время счета одного временного шага составило 0.3 миллисекунды для одного миллиона частиц с двойной точностью (ГрафИТ!, НИВЦ МГУ).
Так как для каждой частицы выполняется приблизительно 250 операций, то производительность одной карты Tesla может быть оценена как 833 ГигаФлопс (0.8 Терафлопс)

О перспективах достижения экзафлопс-производительности.Если...
Взять за основу для рассуждений Tianhe-1A,
Выделить для каждой подобласти один ускоритель Tesla и один универсальный процессор,
Считать, что необходимое количество частиц помещается в оперативную память узла,
Предположить, что время обмена данными между подобластями не превысит имеющегося сейчас,
В таком случае компьютер Tianhe-1A дал бы для метода частиц в ячейках производительность порядка 5.6 PetaFLOPS.
Такая же производительность могла бы быть достигнута при использовании порядка 250 тыс. 4-ядерных процессоров Xeon.

Заключение
1) В настоящее время параллельные методы и алгоритмы недостаточно разработаны, в связи с чем невозможно эффективно использовать существующие вычислительные мощности.
2) Для успешного создания эффективных параллельных алгоритмов и программ необходимо учитывать:
а) специфику задачи и метода;
б) архитектуру вычислительного комплекса.

ЦЕНТР КОЛЛЕКТИВНОГО
ПОЛЬЗОВАНИЯ ССКЦ ПРИ ИВМиМГ СО РАН
Научный руководитель: академик Б.Г. Михайленко
Исполнительный директор: д.т.н. Б.М. Глинский
Зам. исполнительного директора: д.т.н. В.Э. Малышкин
Ученый секретать: к.ф.-м.н. И.Г. Черных
В состав ЦКП ССКЦ входят следующие лаборатории ИВМиМГ:
Лаб. Сибирский суперкомпьютерный центр
Лаб. Синтеза параллельных программ
Лаб. Вычислительной физики
Лаб. Параллельных алгоритмов решения больших задач

ОСНОВНЫЕ ЗАДАЧИ ЦКП ССКЦ
Обеспечение работ институтов СО РАН и университетов Сибири по математическому моделированию в фундаментальных и прикладных исследованиях.
Координация работ по развитию суперкомпьютерных центров Сибири, осуществляемая Советом по супервычислениям при Президиуме СО РАН.
Организация обучения специалистов СО РАН и студентов университетов (ММФ и ФИТ НГУ, НГТУ) методам параллельных вычислений на суперкомпьютерах (поддержка ежегодных зимних и летних школ по параллельному программированию для студентов).
Сотрудничество с INTEL, HP и промышленными организациями, тестирование новых процессоров.
Сетевое взаимодействие с другими Суперкомпьютерными центрами СО РАН, Москвы и других городов России, а также зарубежных стран, совместная разработка технологий распределенных вычислений.

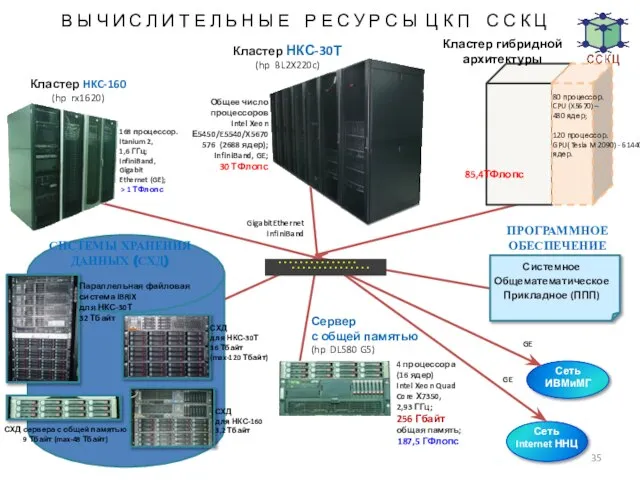
Сервер
с общей памятью
(hp DL580 G5)
GigabitEthernet
InfiniBand
GE
GE
Кластер HKC-160
(hp rx1620)
В Ы Ч И С Л И Т Е Л Ь Н Ы Е Р Е С У Р С Ы Ц К П С С К Ц
Кластер НКС-30Т
(hp BL2X220c)
ПРОГРАММНОЕ
ОБЕСПЕЧЕНИЕ
168 процессор.
Itanium 2,
1,6 ГГц;
InfiniBand,
Gigabit
Ethernet (GE);
> 1 ТФлопс
Общее число
процессоров
Intel Xeon Е5450/E5540/X5670
576 (2688 ядер);
InfiniBand, GE;
30 ТФлопс
4 процессора
(16 ядер)
Intel Xeon Quad
Core Х7350,
2,93 ГГц;
256 Гбайт
общая память;
187,5 ГФлопс
СХД
для НКС-160
3,2 Тбайт
СХД сервера с общей памятью
9 Тбайт (max-48 Тбайт)
СИСТЕМЫ ХРАНЕНИЯ
ДАННЫХ (СХД)
Параллельная файловая система IBRIX
для НКС-30Т
32 Тбайт
СХД
для НКС-30Т
36 Тбайт
(max-120 Тбайт)
Кластер гибридной
архитектуры
80 процессор.
CPU (X5670) –
480 ядер;
120 процессор.
GPU( Tesla M 2090) - 61440 ядер.
85,4ТФлопс

Спасибо за внимание!

Переход к безразмерным переменным
скорость света c = 3x1010 см/с
плотность плазмы n0 = 1014 см-3
плазменная электронная частота ωp = 1.6x106 сек-1

ГРАНТЫ, ПРИ ВЫПОЛНЕНИИ КОТОРЫХ
ИСПОЛЬЗОВАЛИСЬ УСЛУГИ ЦКП ССКЦ В 2010 Г.