Процентные расчеты на каждый день

Сформировать понимание необходимости знаний процентных вычислений для решения большого круга задач, возникающих в повседневной жизни.
Цель:

1) сформировать умения производить процентные вычисления, необходимые для применения в практической деятельности;
1) сформировать умения производить процентные вычисления, необходимые для применения в практической деятельности;
2) решать основные задачи на проценты, применять формулы простых и сложных процентов;
3) показать широту применения процентных расчетов в реальной жизни.
Задачи:

Проценты в прошлом и настоящем.
Зачем нужны проценты.
Основные задачи на проценты:
нахождение процента от числа (величины);
нахождение числа по его проценту;
нахождение процента одного числа от другого.
4. Процентные вычисления в жизненных ситуациях.
распродажа, тарифы, штрафы;
некоторые базовые понятия экономики;
задачи, связанные с банковскими расчетами.
5. Задачи на смеси, сплавы, концентрацию.
6. Задачи с историческими сюжетами.
7. Терминологический словарь.
Процентные расчеты на каждый день

Часть величины принято выражать в процентах. А с величинами человек сталкивается всюду: в практической деятельности, во всех отраслях науки, при выполнении хозяйственных с статистических расчётов. Во многих жизненных ситуациях используется понятие процента.

Дробь 0,01 называется процентом и обозначается 1%.
1%=0,01; 2%=0,02; 45%=0,45; 0,01%=0,0001;
100%=1; 350%=3,5; 25,3%=0.253

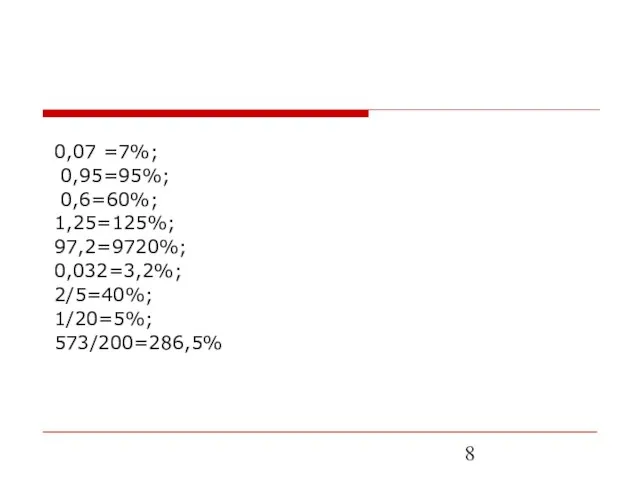
А как выразить дробь(число) в процентах
выразить в процентах числа: 0,07; 0,95; 0,6; 1,25; 97,2; 0,032; 2/5; 1/20; 573/200
Т.к. 1%=1/100,значит,чтобы выразить эти числа в процентах, надо их поделить на 1/100 то есть умножить на 100.

0,07 =7%;
0,95=95%;
0,6=60%;
1,25=125%;
97,2=9720%;
0,032=3,2%;
2/5=40%;
1/20=5%;
573/200=286,5%

Проценты в прошлом и настоящем.
Долгое время под процентами понимались исключительно прибыль или убыток на каждые 100руб. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчётах, статистике, науке и технике. Ныне процент-это частный вид десятичных дробей, сотая доля целого(принимаемого за единицу).

Зачем нужны проценты.
В хозяйственных и статистических расчётах, а также во многих отраслях науки части величин принято выражать в Процентах.
Сложные проценты применяются во многих областях хозяйственной деятельности и бухгалтерского учёта (в банках, сберегательных кассах и т. д.), а также в различных статистических расчётах (в первую очередь при определении среднегодовых темпов относительного прироста или снижения за длительные периоды времени — пятилетки, десятилетия и т. д.).

Основные задачи на проценты: нахождение процента от числа (величины);
Задача 1.В библиотеке 11040 книг на русском и иностранных языках, причём число последних составляет 15% книг на русском языке. Сколько в библиотеке отдельно книг тех и других?
Решение. Пусть х-книг на русском языке книги на иностранном языке составляют 15% книг на русском языке то есть 0,15х.
Так как всего книг в библиотеке 11040, то
х+0,15х=11040
1,15х=11040
х=11040:1,15
х=9600
9600 книг на русском языке
11040-9600=1440
1440-книг на иностранном языке
Ответ:9600кн.,1440кн..

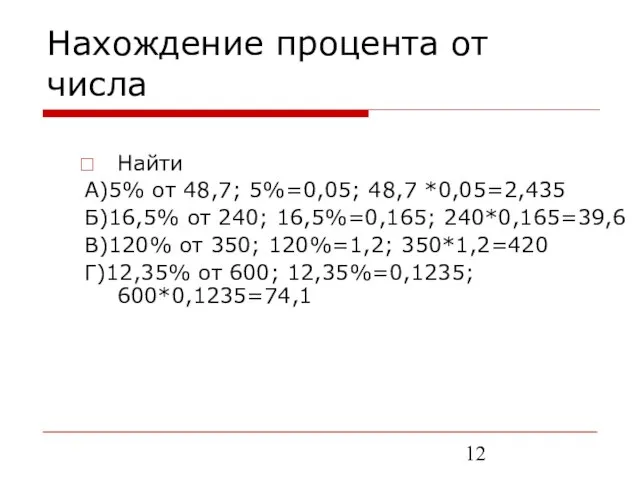
Нахождение процента от числа
Найти
А)5% от 48,7; 5%=0,05; 48,7 *0,05=2,435
Б)16,5% от 240; 16,5%=0,165; 240*0,165=39,6
В)120% от 350; 120%=1,2; 350*1,2=420
Г)12,35% от 600; 12,35%=0,1235; 600*0,1235=74,1

Основные задачи на проценты:
нахождение числа по его проценту;
Если известно. Что а% числа х равно в, то х=в:0,01а
Пример.
3% числа х составляют 150
Х = 150 : 0,03
Х = 5000

Нахождение числа по проценту
Найти число если:
А) 8% его равны 24,8
24,8:8=3,1 составляет 1% числа
искомое число – это 100%, поэтому чтобы найти его надо 3,1*100=310
Итак, 310 искомое число.
Б)3,75% числа равны 75
75:3,75=200
200*100=20000 20000-искомое число

Задача
В классе отсутствовало 4 человека что составило 12,5% всех учащихся класса. Сколько человек в классе.
4:12,5·100=32(ученика)
Ответ: в классе 32 ученика.

От какого числа
а)22,5 составляют 5%
22,5:4*100=450
б)15 составляет 1,2%
15:1,2*100=1250
22,5 составляют 5%от 450
искомое число 1250

Процентное отношение
1.Какой процент от 1,5т составляют 1.2 т
1,5т составляет 100% зависимость
1,2т составляет Х% прямая
пропорциональная значит, 15:1,2=100:х х=1,2•100:15
х=8, 8%составляет 1.2т от 1,5т
Ответ:8%

А можно было процентное отношение чисел 1.2 и 15 вычислить иначе
Первое число разделить на второе
Полученное частное выразить в процентах
1,2:15=0,08=8%

В классе было 25 учащихся. Из них 15 мальчиков. Сколько процентов от всех учащихся составляют мальчики?
15:25•100=60%
60% учащихся класса - мальчики.
Ответ: 60%

Процентные вычисления в жизненных ситуациях: распродажа
Задача.
Зонт стоил 360 р. В ноябре цена зонта была снижена на 15%, а в декабре ещё на 10%. Какой стала стоимость зонта в декабре?
Решение.
Стоимость зонта в ноябре составляла 85% от 360 р.,т.е. 360*0,85=306 р.Второе снижение цены происходило по отношению к новой цене зонта; Теперь следует искать 90% от 306 р. Т.е. 306*0,9=275,4 р.
Ответ.23.5%

Процентные вычисления в жизненных ситуациях: тарифы
Задача
В газете сообщается, что с 10 июня согласно новым тарифам стоимость отправления почтовой открытки составит 3р.15коп. Вместо 2р.27коп.Соответствует ли рост цен на услуги почтовой связи росту цен на товары в этом году, который составляет 14,5%
Решение
Разность тарифов составляет 0,4 р., а её отношение к старому тарифу равно 0,14545…Выразив это отношение в процентах, получим примерно 14,5%
Ответ. Да, соответствует.

Процентные вычисления в жизненных ситуациях: штрафы
Задача
Занятия ребенка в музыкальной школе родители оплачивают в сбербанке, внося ежемесячно 250р.Оплата должна производиться до 15 числа каждого месяца, после чего за каждый просроченный день начисляется пеня в размере 4% от суммы оплаты занятий за один месяц. Сколько придется заплатить родителям, если они просрочат оплату на неделю?
Решение.
Так как 4% от 250р. Составляют 10р., то за каждый просроченный день сумма оплаты будет увеличиваться на 10р.Если родители просрочат оплату на день, то им придется заплатить 250+10=260р.
На неделю 250+10*7=320р.
Ответ: 320р.

Две ремонтные мастерские в течение недели должны отремонтировать по плану 18 моторов. Первая мастерская выполнила план на 120%, а вторая - на 125%, поэтому за неделю они отремонтировали 22 мотора. Какой план по ремонту на неделю имела каждая мастерская?
Пусть х моторов за неделю должна была отремонтировать первая мастерская, тогда вторая 18-х моторов.
Первая мастерская выполнила задание на 120%, то есть сделала 1,2 этого задания(120%=1,20), она отремонтировала 1,2х моторов. Вторая выполнила задание на 125% т.е отремонтировала 1,25(18-х) моторов
Так как вместе они отремонтировали 22 мотора, то
1,2х+1,25(18-х)=22
1,2х+22,5-1,25х=22
1,2х-1,25х=22-22,5
-0,05х=-0,5
Х=10
10 моторов должна была отремонтировать первая бригада, тогда вторая (18-10=8)-8моторов
Ответ: 10 моторов и 8 моторов.

Процентные вычисления в жизненных ситуациях: задачи, связанные с банковскими расчетами
Задача
Банк выплачивает вкладчикам каждый год 85 от внесенной суммы. Клиент сделал вклад в размере 200000 р. Какая сумма будет на его счете через 5 лет, через 10 лет?
Решение
Используя формулу:
Sn=So(1+n*p/100)
S5=200000(1+5*8/100)=280000 (p.)
S10=200000(1+10*8/100)=360000 (p.)
Ответ: 280000 р., 360000 р.

Задачи на смеси, сплавы, концентрацию
В различные сборники заданий для подготовки к экзаменам входят задачи, решение которых связано с понятиями «концентрация» и «процентное содержание». Обычно в их условиях речь идет о составлении сплавов, растворов или смесей двух или более веществ.
У многих учеников эти задачи вызывают затруднения. Вероятно, это связано с тем, что таким задачам в школьном курсе математики уделяется совсем мало внимания.

Задачи на концентрацию
V = V1 + V2,
m = m1 + m2
с = а*100%, где с – смесь, а – доля чистого вещества в смеси
n = mв/mp, где n - концентрация, mв – масса вещества в растворе, mp – масса всего раствора.
Процентным содержанием чистого вещества в смеси с называют его долю, выраженную процентным отношением: с = а 100 %, а = с/100%.
Задачи на концентрацию

Задача.
Имеются два куска сплава меди и цинка с процентным содержанием меди 42% и 65% соответственно. В каком отношении нужно взять эти сплавы, чтобы переплавив, получить сплав, содержащий 50% меди?
Решение. Изобразим схематически условие задачи:
Задачи на концентрацию

Решение.
Можем составить уравнение: 0,42х + 0,65у = 0,5(х + у). В этом уравнении 2 неизвестных, а в задаче требуется найти их отношение х/у. Решая уравнение, получим 42х + 65у = 50*(х + у),
15у = 8х. х/у = 15/8. Следовательно, нужно взять первый и второй сплавы в отношении 15 к 8.
Ответ: нужно взять первый и второй сплавы в отношении 15 к 8.

Задача. Сплав состоит из 64,8% меди; 32,8% цинка и 2,4% свинца. Сколько нужно взять меди, цинка и свинца, чтобы получить сплав массой в 0,75т?
Решение.
0,75т=750кг; 64,8%=0,648;
32,85=0,328; 2,4%=0,024.
750*0,648=486(кг)-масса меди в сплаве.
750*0,328=246(кг)-масса цинка.
750*0,024=189(кг)-масса свинца.
Ответ: 486кг,246кг,189кг.

Задачи с историческими сюжетами
Задача
Один небогатый римлянин взял в долг у заимодавца 50 сестерциев. Заимодавец поставил условие: «Ты вернешь мне в установленный срок 50 сестерциев и ещё 20% от этой суммы». Сколько сестерциев должен отдать небогатый римлянин заимодавцу возвращая долг?
Ответ: 60 сестерциев.

Терминологический словарь
ПРОЦЕНТ (от лат. pro centum — за сто), сотая доля числа, обозначается знаком %
Бюджет – перечень доходов и расходов, финансовый план, сопоставляющий ожидаемые доходы и расходы.
Инфляция – падение ценности или покупательной способности денег.
Налоги – обязательные платежи, взимаемые государством с граждан. Налоги – один из источников дохода государственного бюджета.
Пеня – вид неустойки. Исчисляется в процентах от суммы неисполненного или ненадлежаще исполненного обязательства и уплачивается за каждый день просрочки.
Тарифы – система ставок, по которым взимается плата за услуги. Наиболее распространены тарифы транспортные – за перевозку грузов, багажа.

Повторили понятие «процент», основные понятия связанные с процентами;
выделили основные типы задач;
научились решать основные задачи на проценты;
научились применять формулу сложных процентов;
показали широту применения процентных вычислений в реальной жизни.
Подведем итоги: