Проекции плоскости

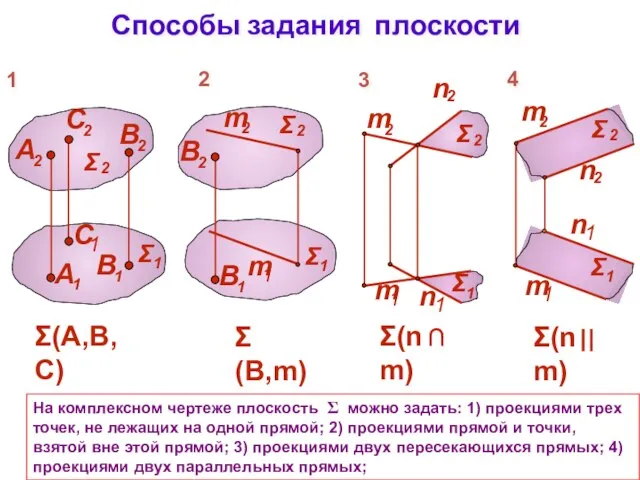
Способы задания плоскости
На комплексном чертеже плоскость Σ можно задать: 1) проекциями трех точек, не лежащих на одной прямой; 2) проекциями прямой и точки, взятой вне этой прямой; 3) проекциями двух пересекающихся прямых; 4) проекциями двух параллельных прямых;

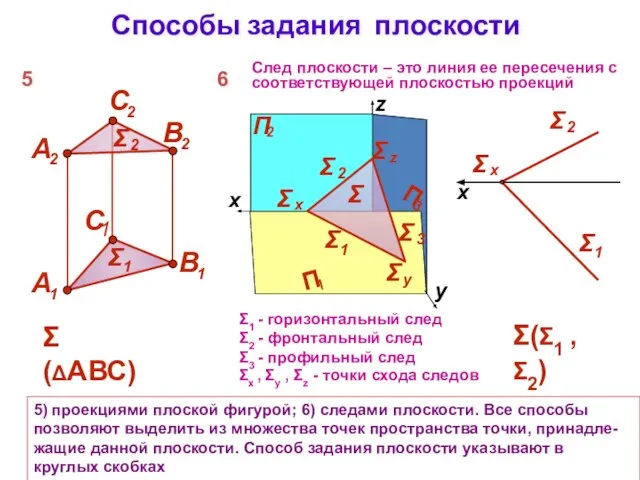
Способы задания плоскости
5) проекциями плоской фигурой; 6) следами плоскости. Все способы позволяют выделить из множества точек пространства точки, принадле-жащие данной плоскости. Способ задания плоскости указывают в круглых скобках
След плоскости – это линия ее пересечения с соответствующей плоскостью проекций

Положение плоскости относительно плоскостей проекций
Плоскость общего положения наклонена ко всем плоскостям проекций
Плоскость частного положения перпендикулярна или параллельна одной из плоскостей проекций
Горизонтально проецирующая плоскость ⊥ П1
Фронтально проецирующая плоскость ⊥ П2 Профильно проецирующая плоскость ⊥ П3
Горизонтальная плоскость ⎢⎢ П1
Фронтальная плоскость ⎢⎢ П2
Профильная плоскость ⎢⎢П3
Плоскость, перпендикулярная одной из плоскостей проекций, называется проецирующей плоскостью:
Плоскость, параллельная плоскости проекций, назы-вается плоскостью уровня (дважды проецирующей):

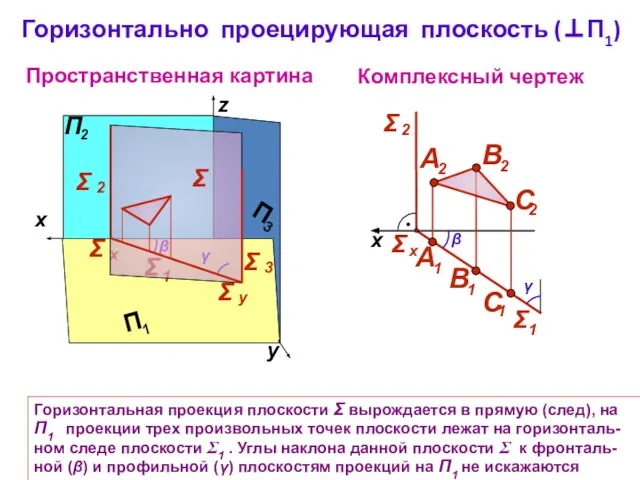
Горизонтально проецирующая плоскость (⊥П1)
Пространственная картина
Комплексный чертеж
y
z
Горизонтальная проекция плоскости Σ вырождается в прямую (след), на П1 проекции трех произвольных точек плоскости лежат на горизонталь-ном следе плоскости Σ1 . Углы наклона данной плоскости Σ к фронталь-ной (β) и профильной (γ) плоскостям проекций на П1 не искажаются
β
γ
Σ

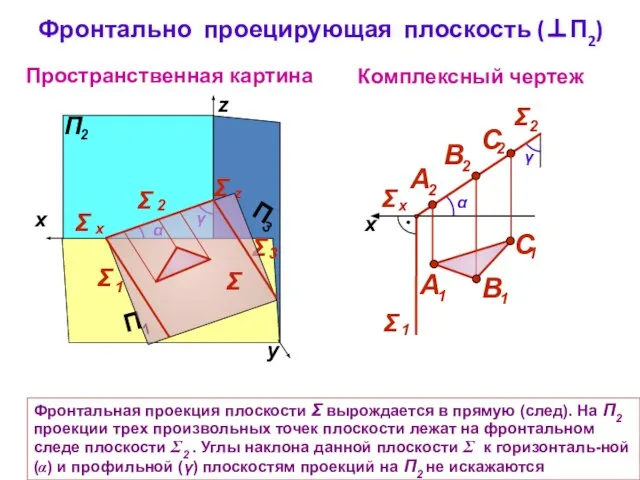
Фронтально проецирующая плоскость (⊥П2)
Комплексный чертеж
y
z
Пространственная картина
γ
α
Σ
Фронтальная проекция плоскости Σ вырождается в прямую (след). На П2 проекции трех произвольных точек плоскости лежат на фронтальном следе плоскости Σ2 . Углы наклона данной плоскости Σ к горизонталь-ной (α) и профильной (γ) плоскостям проекций на П2 не искажаются

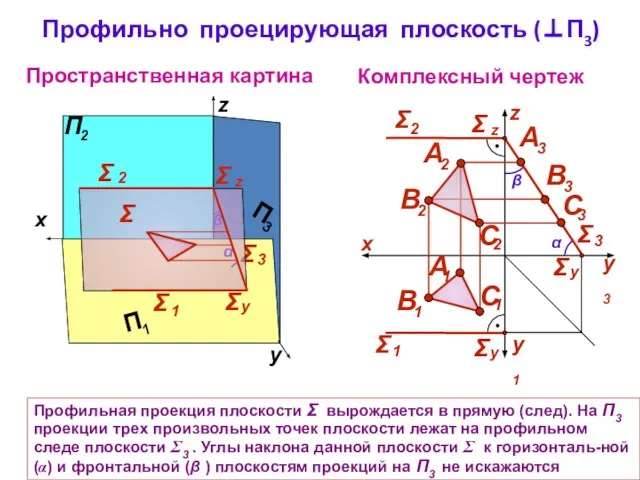
Профильно проецирующая плоскость (⊥П3)
Комплексный чертеж
z
Пространственная картина
α
β
Σ
Профильная проекция плоскости Σ вырождается в прямую (след). На П3 проекции трех произвольных точек плоскости лежат на профильном следе плоскости Σ3 . Углы наклона данной плоскости Σ к горизонталь-ной (α) и фронтальной (β ) плоскостям проекций на П3 не искажаются

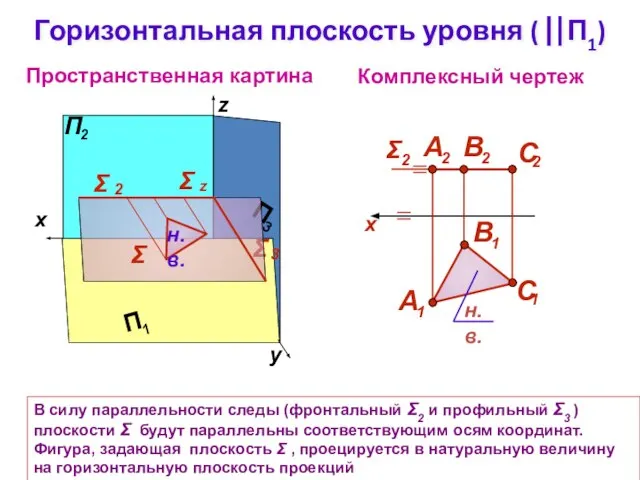
Горизонтальная плоскость уровня ( ⎢⎢П1)
Комплексный чертеж
z
Σ
Пространственная картина
В силу параллельности следы (фронтальный Σ2 и профильный Σ3 ) плоскости Σ будут параллельны соответствующим осям координат. Фигура, задающая плоскость Σ , проецируется в натуральную величину на горизонтальную плоскость проекций

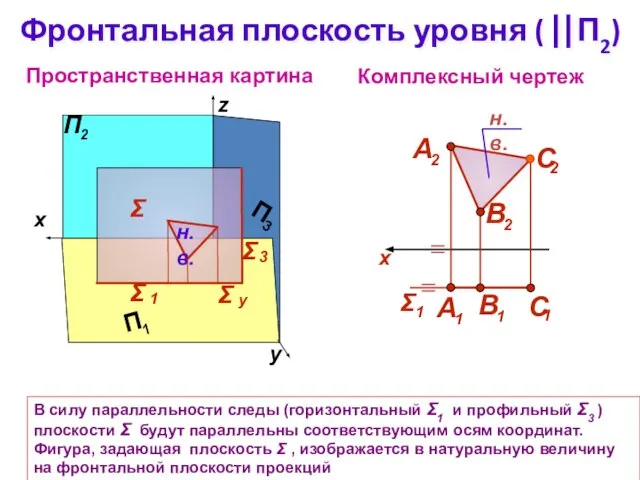
Фронтальная плоскость уровня ( ⎢⎢П2)
Комплексный чертеж
z
Пространственная картина
Σ
В силу параллельности следы (горизонтальный Σ1 и профильный Σ3 ) плоскости Σ будут параллельны соответствующим осям координат. Фигура, задающая плоскость Σ , изображается в натуральную величину на фронтальной плоскости проекций

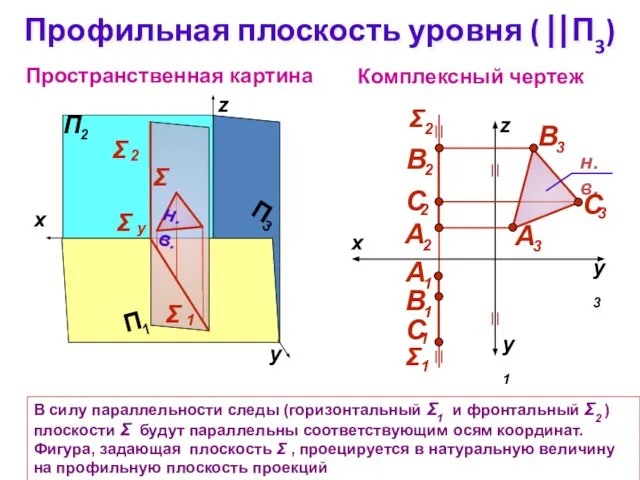
Профильная плоскость уровня ( ⎢⎢П3)
Комплексный чертеж
z
Пространственная картина
Σ
В силу параллельности следы (горизонтальный Σ1 и фронтальный Σ2 ) плоскости Σ будут параллельны соответствующим осям координат. Фигура, задающая плоскость Σ , проецируется в натуральную величину на профильную плоскость проекций

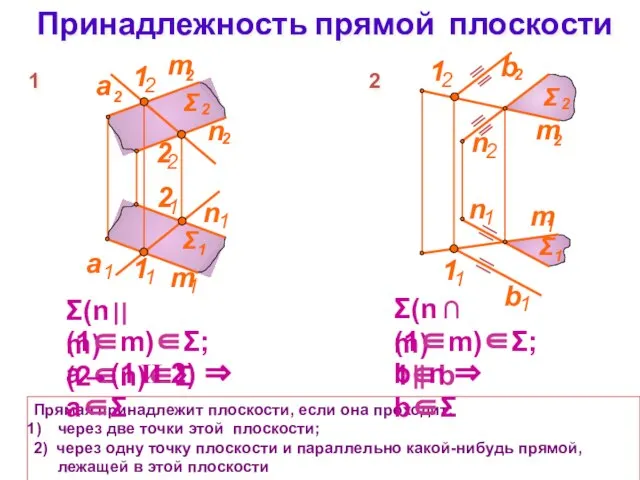
Принадлежность прямой плоскости
Прямая принадлежит плоскости, если она проходит:
через две точки этой плоскости;
2) через одну точку плоскости и параллельно какой-нибудь прямой, лежащей в этой плоскости
Σ(n⎟⎟ m)
1
(1∈m)∈Σ; (2∈n)∈Σ
а→(1 И 2) ⇒ а∈Σ
2
Σ(n ∩ m)
(1∈m)∈Σ; 1∈b
b⎟⎟ n ⇒ b∈Σ

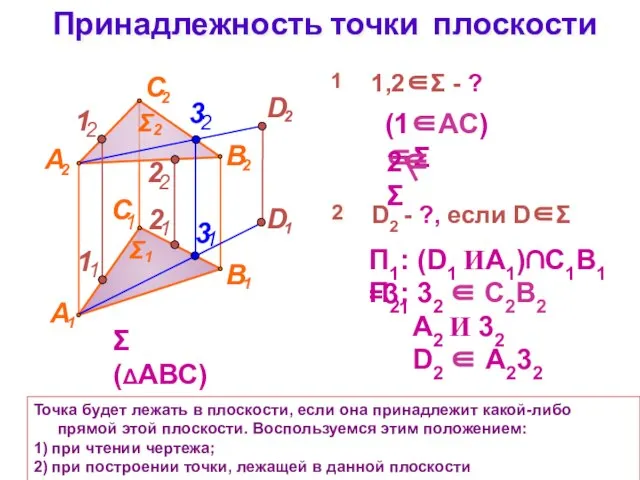
Принадлежность точки плоскости
Точка будет лежать в плоскости, если она принадлежит какой-либо прямой этой плоскости. Воспользуемся этим положением:
1) при чтении чертежа;
2) при построении точки, лежащей в данной плоскости
(1∈АС)∈Σ
П1: (D1 ИA1)∩С1В1 =31
Σ(ΔАВС)
1
П2: 32 ∈ C2B2
1,2∈Σ - ?
А2 И 32
D2 ∈ А232

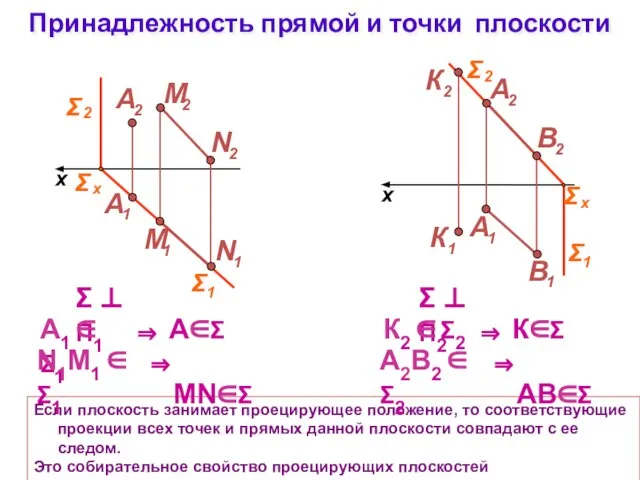
Принадлежность прямой и точки плоскости
Если плоскость занимает проецирующее положение, то соответствующие проекции всех точек и прямых данной плоскости совпадают с ее следом.
Это собирательное свойство проецирующих плоскостей
Σ ⊥ П1
x
Σ ⊥ П2
x

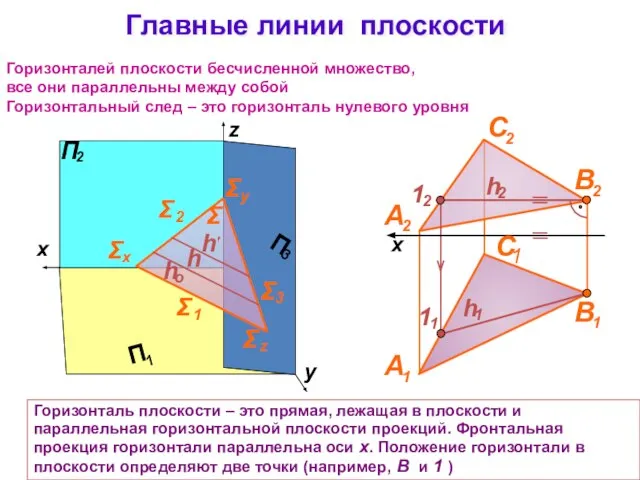
Главные линии плоскости
Горизонталь плоскости – это прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций. Фронтальная проекция горизонтали параллельна оси x. Положение горизонтали в плоскости определяют две точки (например, В и 1 )
Σ
Горизонталей плоскости бесчисленной множество,
все они параллельны между собой
Горизонтальный след – это горизонталь нулевого уровня
x

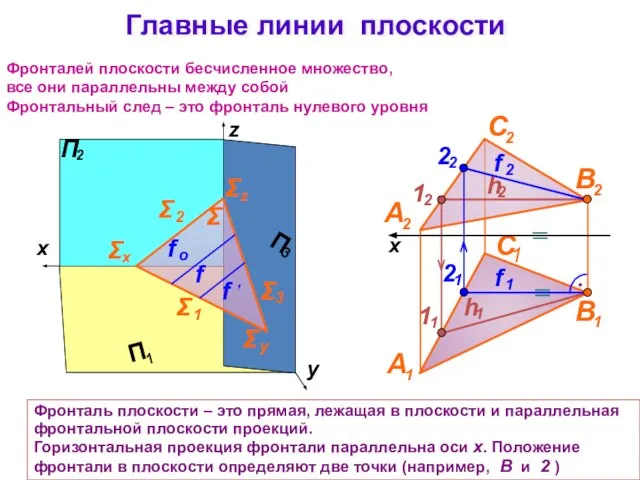
Главные линии плоскости
Σ
Фронталей плоскости бесчисленное множество,
все они параллельны между собой
Фронтальный след – это фронталь нулевого уровня
Фронталь плоскости – это прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций.
Горизонтальная проекция фронтали параллельна оси x. Положение фронтали в плоскости определяют две точки (например, В и 2 )
x

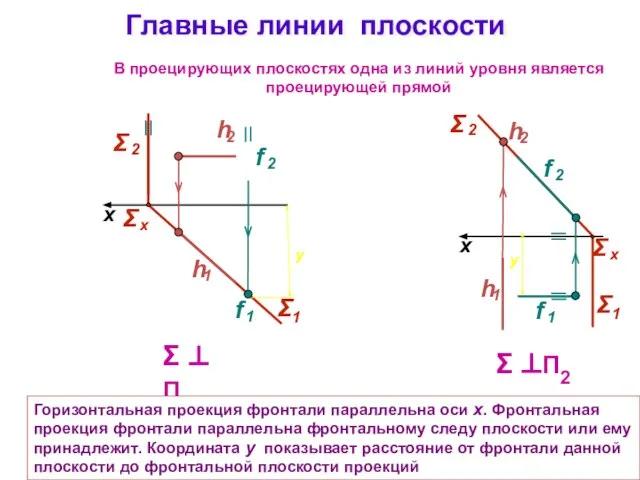
Главные линии плоскости
Σ ⊥ П1
x
Σ ⊥П2
x
В проецирующих плоскостях одна из линий уровня является проецирующей прямой
Горизонтальная проекция фронтали параллельна оси x. Фронтальная проекция фронтали параллельна фронтальному следу плоскости или ему принадлежит. Координата y показывает расстояние от фронтали данной плоскости до фронтальной плоскости проекций

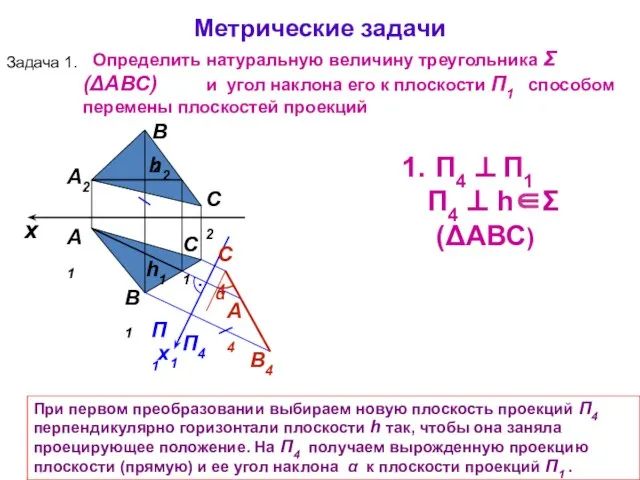
А1
А2
При первом преобразовании выбираем новую плоскость проекций П4 перпендикулярно горизонтали плоскости h так, чтобы она заняла проецирующее положение. На П4 получаем вырожденную проекцию плоскости (прямую) и ее угол наклона α к плоскости проекций П1 .
Определить натуральную величину треугольника Σ(ΔАВС) и угол наклона его к плоскости П1 способом перемены плоскостей проекций
B1
C2
B2
C1
x
П4 ⊥ П1
П4 ⊥ h∈Σ(ΔАВС)
Метрические задачи
Задача 1.

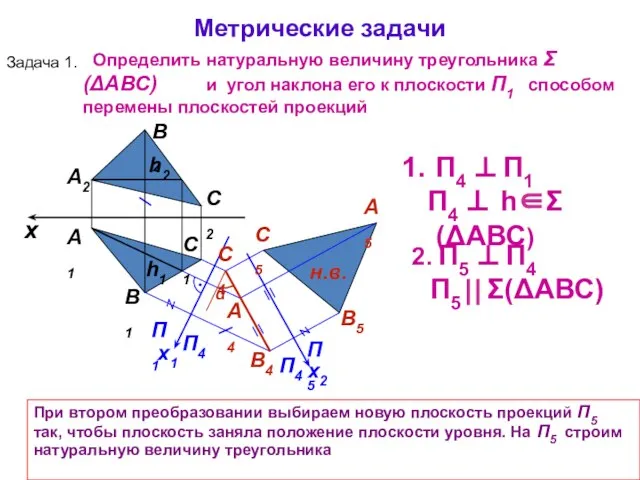
x
А1
А2
П1
П4
x1
П4 ⊥ П1
П4 ⊥ h∈Σ(ΔАВС)
2. П5 ⊥ П4
П5⎟⎟ Σ(ΔАВС)
При втором преобразовании выбираем новую плоскость проекций П5 так, чтобы плоскость заняла положение плоскости уровня. На П5 строим натуральную величину треугольника
h1
h2
B1
C2
B2
А4
C1
В4
C4
α
Метрические задачи
Задача 1.
Определить натуральную величину треугольника Σ(ΔАВС) и угол наклона его к плоскости П1 способом перемены плоскостей проекций

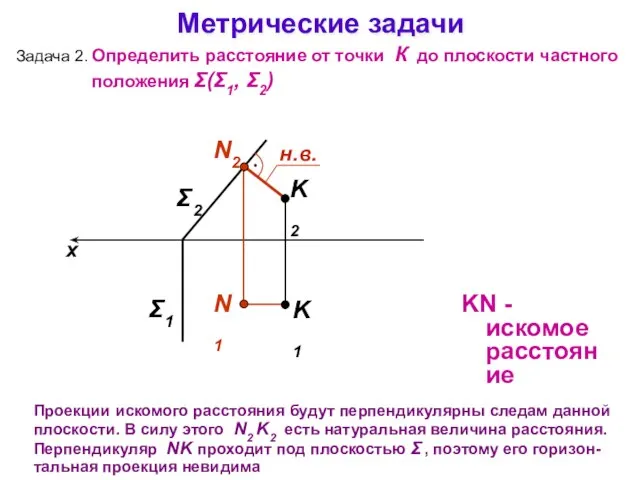
Метрические задачи
Задача 2.
Определить расстояние от точки К до плоскости частного положения Σ(Σ1, Σ2)
x
Проекции искомого расстояния будут перпендикулярны следам данной плоскости. В силу этого N2 K2 есть натуральная величина расстояния. Перпендикуляр NK проходит под плоскостью Σ , поэтому его горизон-тальная проекция невидима
Σ 2
K1
Σ 1
K2
KN - искомое расстояние

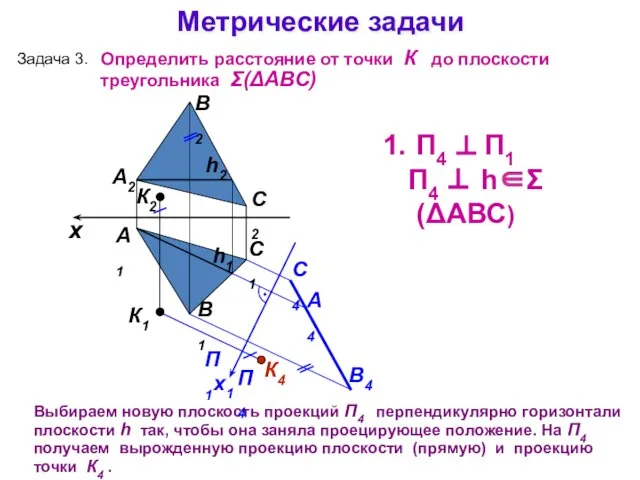
Метрические задачи
А1
А2
Выбираем новую плоскость проекций П4 перпендикулярно горизонтали плоскости h так, чтобы она заняла проецирующее положение. На П4 получаем вырожденную проекцию плоскости (прямую) и проекцию точки К4 .
Задача 3.
B1
C2
B2
C1
x
П4 ⊥ П1
П4 ⊥ h∈Σ(ΔАВС)
К1
К2
Определить расстояние от точки К до плоскости треугольника Σ(ΔАВС)