Содержание
- 2. Взаимное положение прямой и плоскости, двух плоскостей Прямая принадлежит плоскости (см. тема 3): все точки прямой
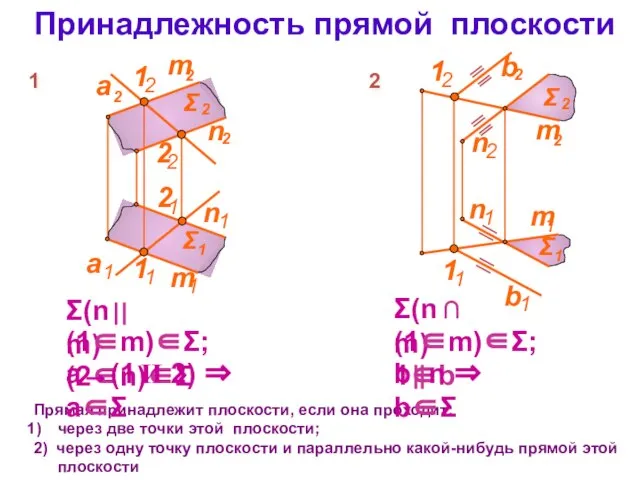
- 3. Принадлежность прямой плоскости Прямая принадлежит плоскости, если она проходит: через две точки этой плоскости; 2) через
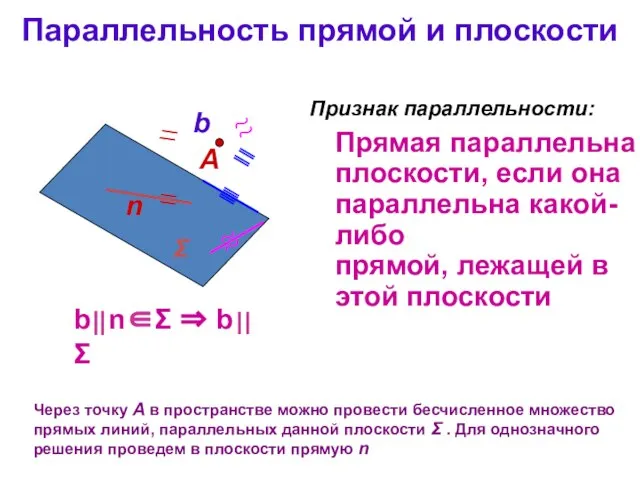
- 4. Параллельность прямой и плоскости Через точку А в пространстве можно провести бесчисленное множество прямых линий, параллельных
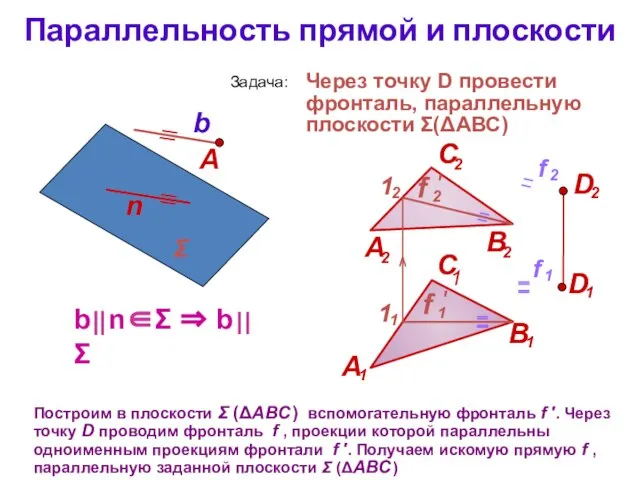
- 5. Параллельность прямой и плоскости Построим в плоскости Σ (ΔАВС ) вспомогательную фронталь f ′. Через точку
- 6. Параллельность прямой и плоскости Σ(Σ1, Σ2) x Если прямая а параллельна плоскости общего положения, то в
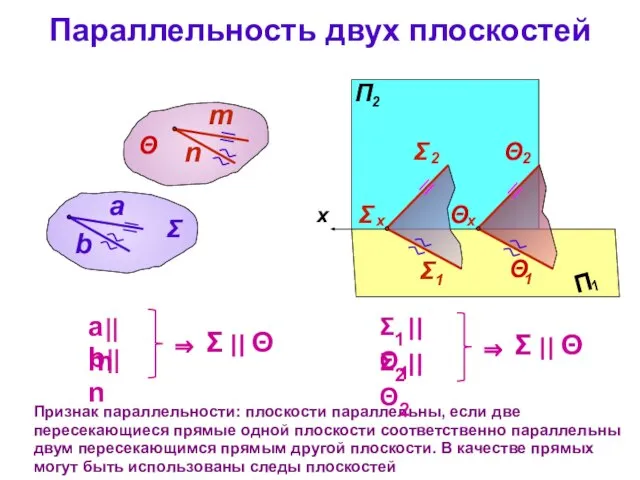
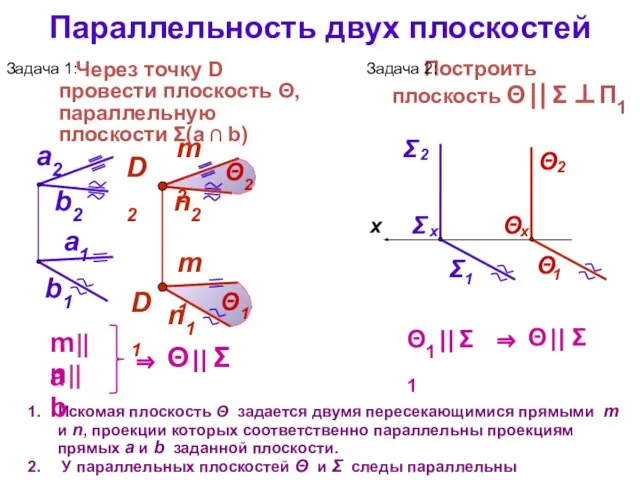
- 7. Параллельность двух плоскостей Признак параллельности: плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум
- 8. Параллельность двух плоскостей Искомая плоскость Θ задается двумя пересекающимися прямыми m и n, проекции которых соответственно
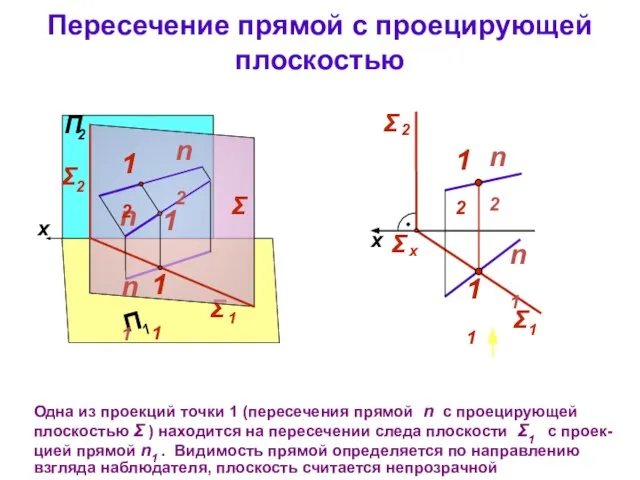
- 9. Σ Пересечение прямой с проецирующей плоскостью Одна из проекций точки 1 (пересечения прямой n с проецирующей
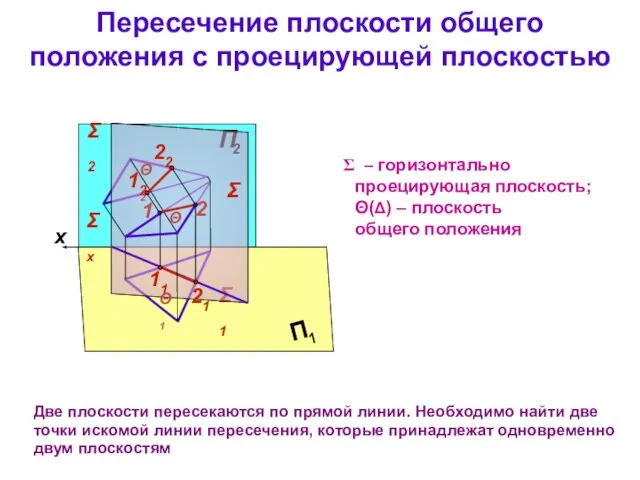
- 10. Пересечение плоскости общего положения с проецирующей плоскостью Две плоскости пересекаются по прямой линии. Необходимо найти две
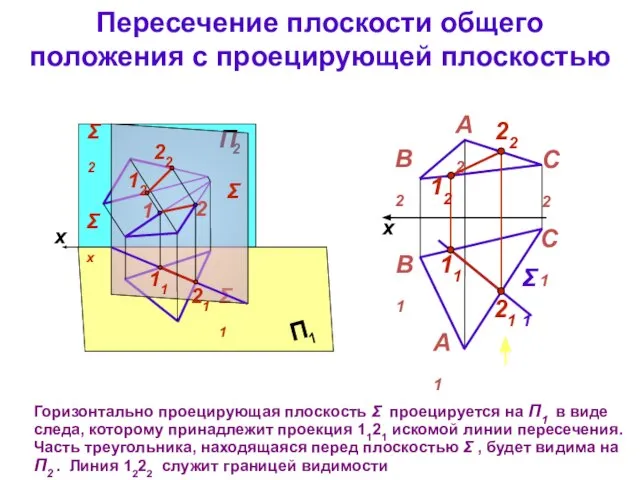
- 11. Пересечение плоскости общего положения с проецирующей плоскостью Горизонтально проецирующая плоскость Σ проецируется на П1 в виде
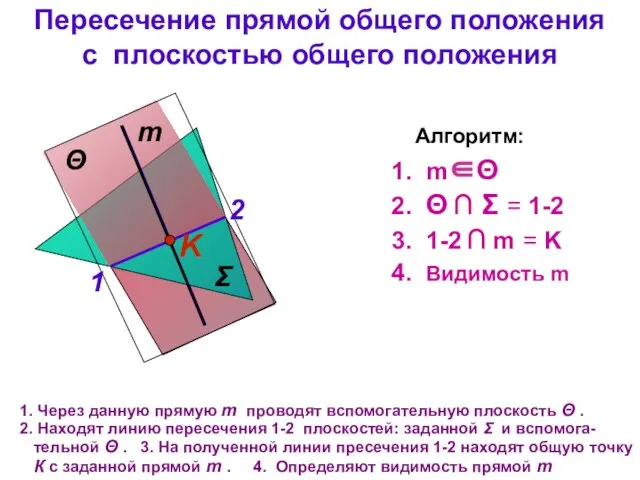
- 12. Пересечение прямой общего положения с плоскостью общего положения Σ m Через данную прямую m проводят вспомогательную
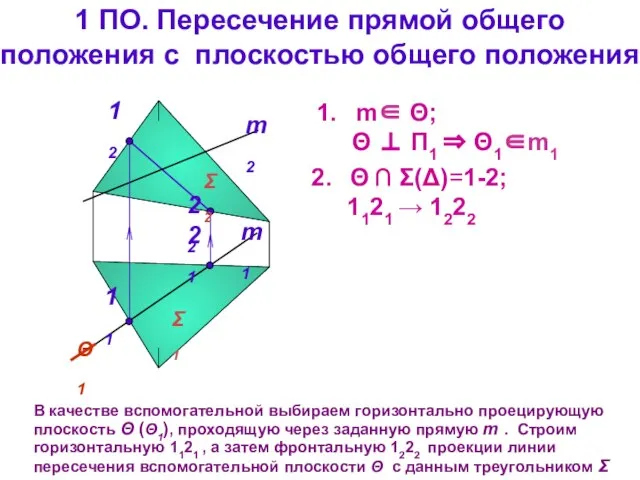
- 13. 1 ПО. Пересечение прямой общего положения с плоскостью общего положения m1 m2 В качестве вспомогательной выбираем
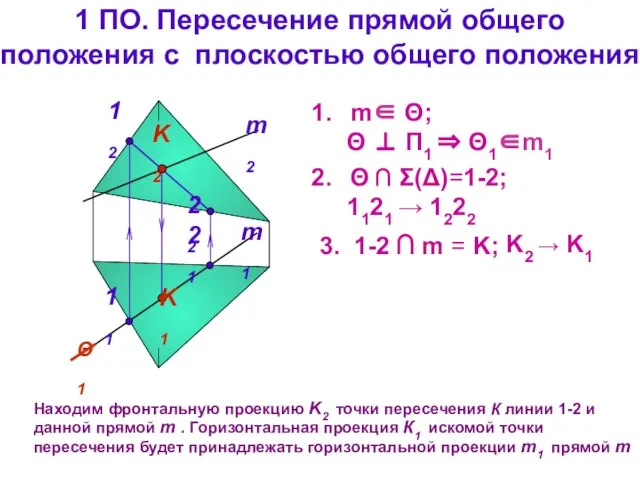
- 14. 1 ПО. Пересечение прямой общего положения с плоскостью общего положения m1 m2 Находим фронтальную проекцию K2
- 16. Скачать презентацию


 Сервис Мечты
Сервис Мечты Основи формування і реєстраціi корисного сигналу в діапазоні
Основи формування і реєстраціi корисного сигналу в діапазоні Комплексная система автоматизации
Комплексная система автоматизации Телепорт
Телепорт Осторожно! Сосульки
Осторожно! Сосульки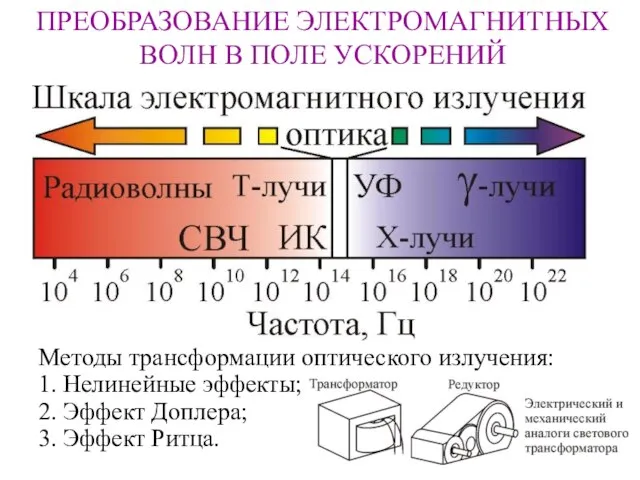 ПРЕОБРАЗОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ПОЛЕ УСКОРЕНИЙ
ПРЕОБРАЗОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ПОЛЕ УСКОРЕНИЙ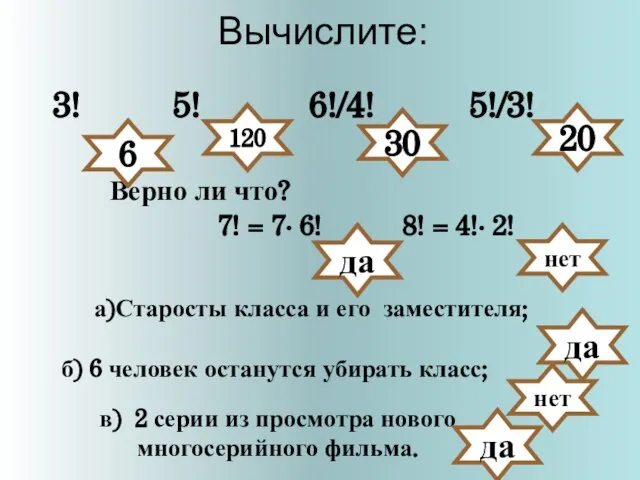 Примеры комбинаторных задач (9 класс)
Примеры комбинаторных задач (9 класс) Решение логических задач из курса кибернетики
Решение логических задач из курса кибернетики Бедность
Бедность Nocturnal eczema: Review of sleep and circadian rhythms
Nocturnal eczema: Review of sleep and circadian rhythms Microsoft Office Word 2007
Microsoft Office Word 2007 Международное сотрудничество в освоении космического пространства
Международное сотрудничество в освоении космического пространства Золото
Золото Презентация на тему Загадки о диких животных
Презентация на тему Загадки о диких животных Королева оркестра
Королева оркестра Экологическое просвещение в творчествеВладимира Алексеевича Чивилихина
Экологическое просвещение в творчествеВладимира Алексеевича Чивилихина Ҳозирги замон ҳуқуқи ва унинг моҳияти ҳақидаги концепциялар
Ҳозирги замон ҳуқуқи ва унинг моҳияти ҳақидаги концепциялар Образ Чичикова в поэме "Мертвые души"
Образ Чичикова в поэме "Мертвые души" Табір "Світанок"
Табір "Світанок" Презентация на тему Уфа – столица Башкортостана
Презентация на тему Уфа – столица Башкортостана Онтология
Онтология  Источники загрязнения окружающей среды
Источники загрязнения окружающей среды Project_A
Project_A Типы связи слов в словосочетании
Типы связи слов в словосочетании Всероссийский флешмоб Голубь мира
Всероссийский флешмоб Голубь мира Работа головного мозга находится в прямой зависимости от качества нашего питания, чем оно лучше, тем выше наши интеллектуальные во
Работа головного мозга находится в прямой зависимости от качества нашего питания, чем оно лучше, тем выше наши интеллектуальные во БИОСИНТЕЗ
БИОСИНТЕЗ Сусымалы компоненттерді мөлшерлеу мен қоспалау желісі. Дарис 12
Сусымалы компоненттерді мөлшерлеу мен қоспалау желісі. Дарис 12