Содержание
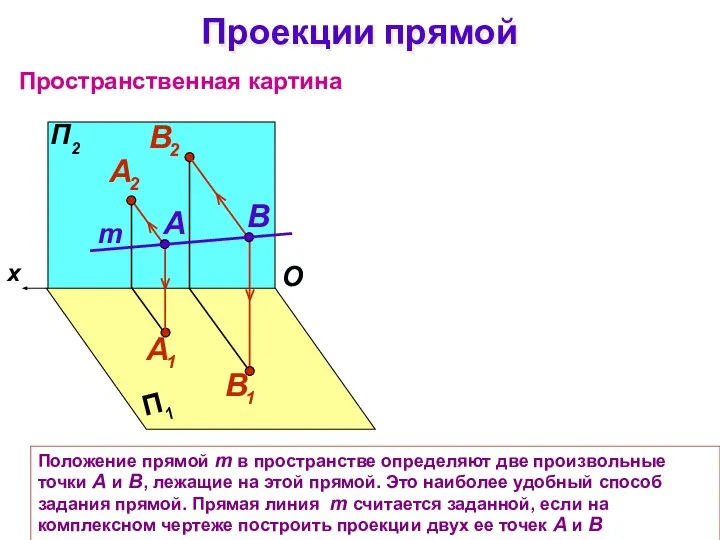
- 2. Положение прямой m в пространстве определяют две произвольные точки А и В, лежащие на этой прямой.
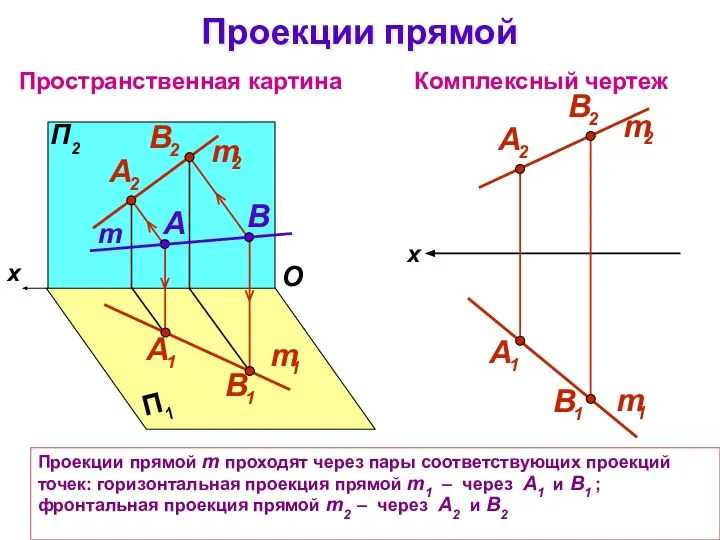
- 3. Проекции прямой m проходят через пары соответствующих проекций точек: горизонтальная проекция прямой m1 – через А1
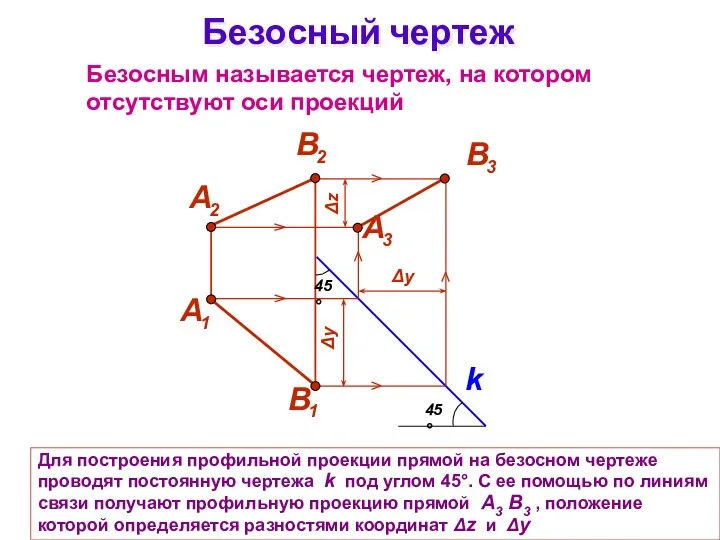
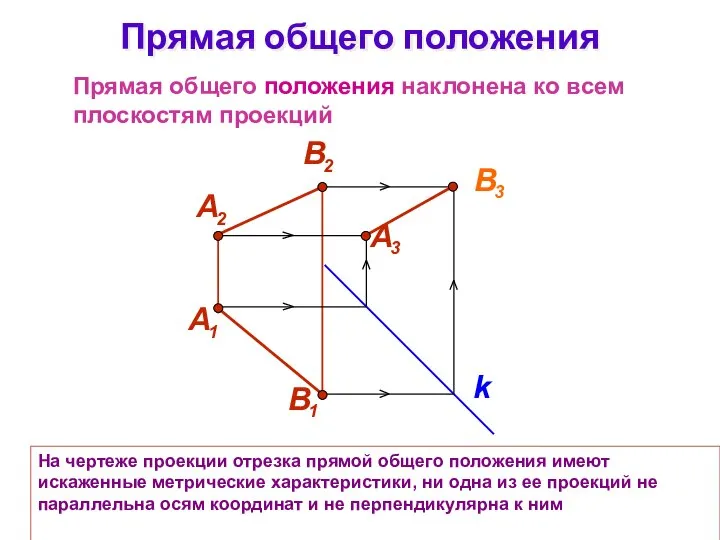
- 4. Для построения профильной проекции прямой на безосном чертеже проводят постоянную чертежа k под углом 45°. С
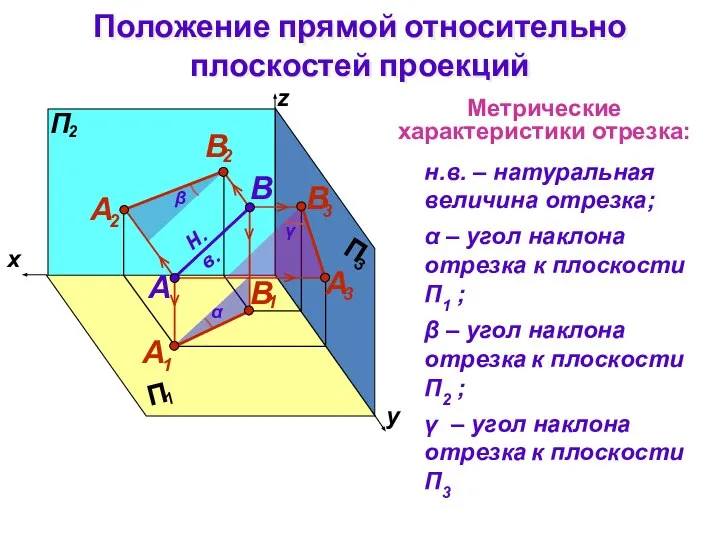
- 5. Метрические характеристики отрезка: н.в. – натуральная величина отрезка; α – угол наклона отрезка к плоcкости П1
- 6. На чертеже проекции отрезка прямой общего положения имеют искаженные метрические характеристики, ни одна из ее проекций
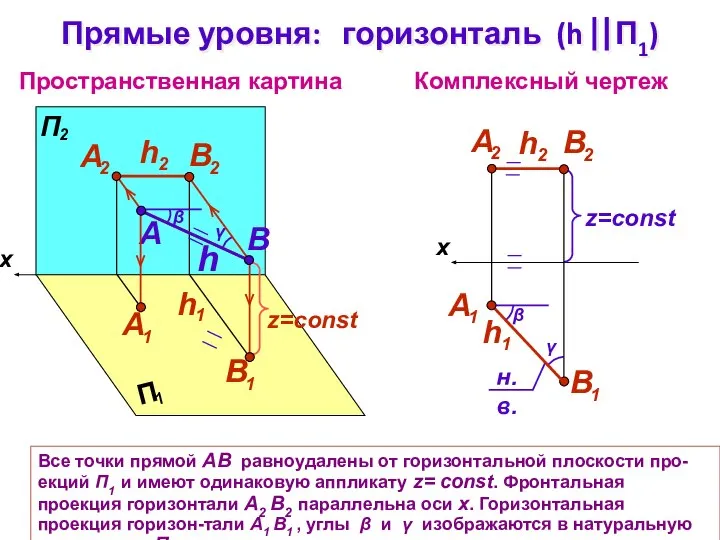
- 7. У прямой частного положения на комплексном чертеже определяются натуральные величины каких-либо ее характеристик. Прямая уровня про-ецируется
- 8. Все точки прямой АВ равноудалены от горизонтальной плоскости про-екций П1 и имеют одинаковую аппликату z= const.
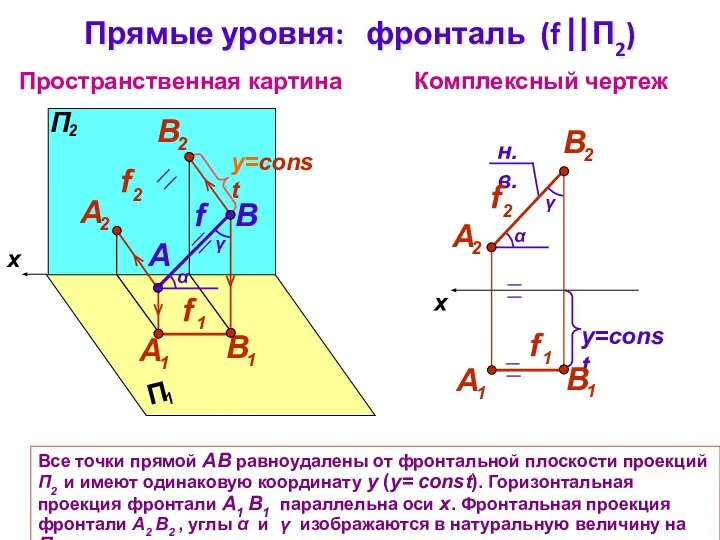
- 9. Пространственная картина Комплексный чертеж x B f Прямые уровня: фронталь (f ⎢⎢П2) A Все точки прямой
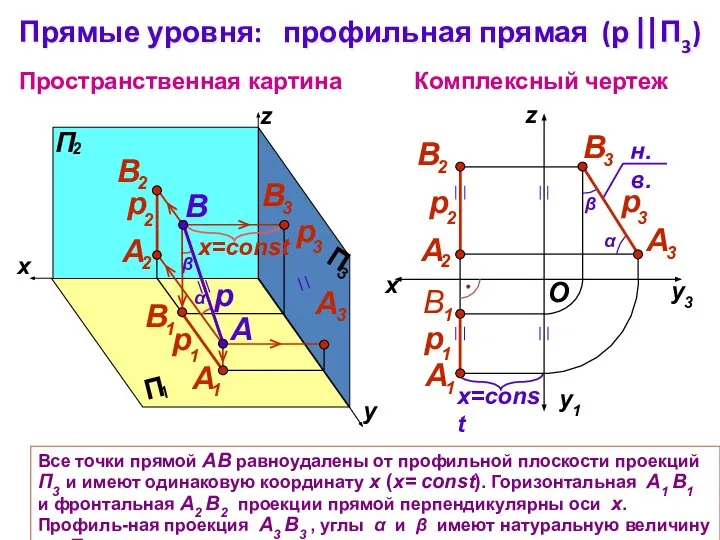
- 10. Все точки прямой АВ равноудалены от профильной плоскости проекций П3 и имеют одинаковую координату х (х=
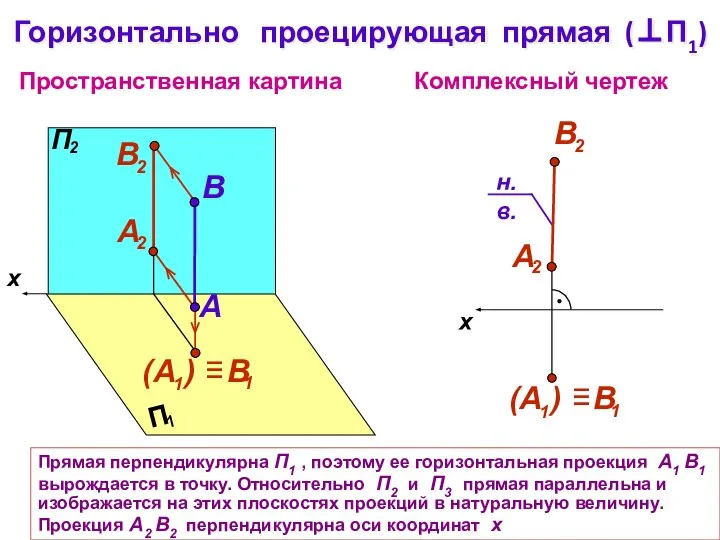
- 11. x Пространственная картина Комплексный чертеж A B Горизонтально проецирующая прямая (⊥П1) Прямая перпендикулярна П1 , поэтому
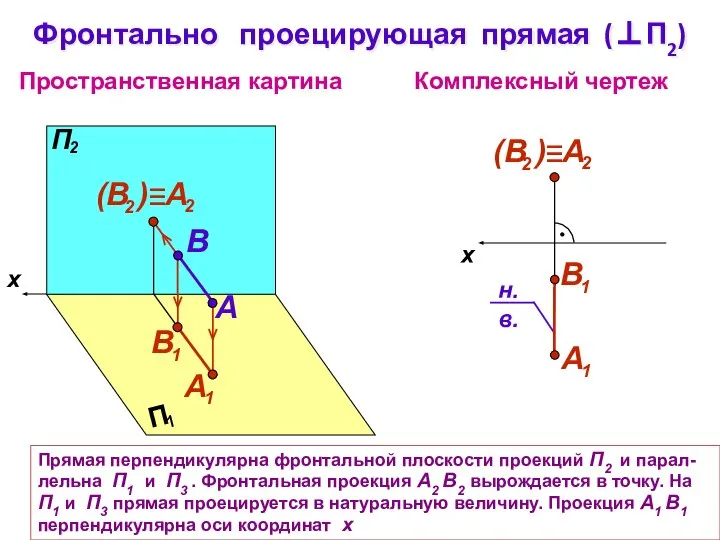
- 12. Прямая перпендикулярна фронтальной плоскости проекций П2 и парал-лельна П1 и П3 . Фронтальная проекция А2 В2
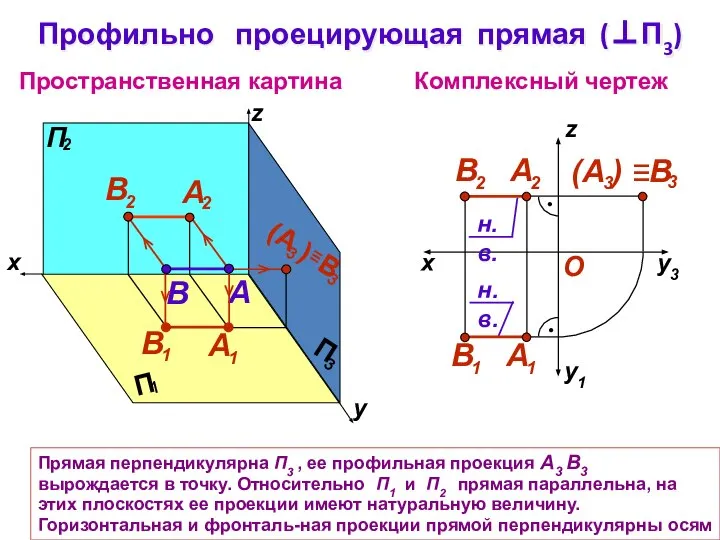
- 13. Прямая перпендикулярна П3 , ее профильная проекция А3 В3 вырождается в точку. Относительно П1 и П2
- 14. Преобразование чертежа прямой общего положения
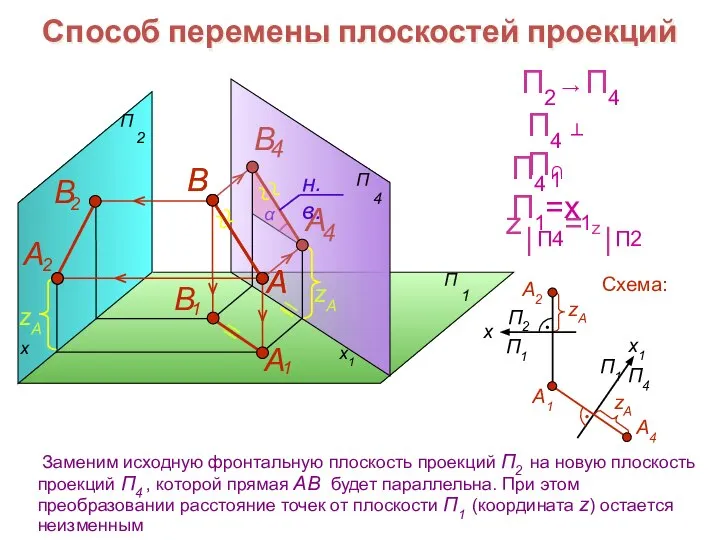
- 15. x1 Заменим исходную фронтальную плоскость проекций П2 на новую плоскость проекций П4 , которой прямая АВ
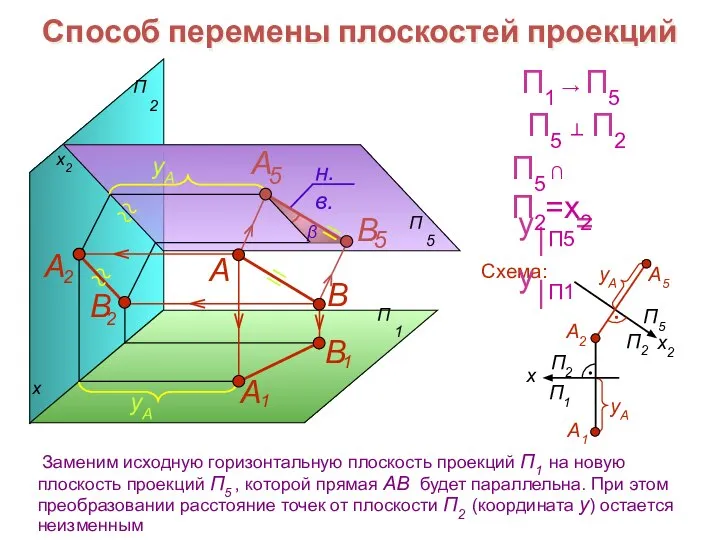
- 16. Способ перемены плоскостей проекций x x2 В А Схема: П1 → П5 y⎪П5= y⎪П1 П5 ⊥
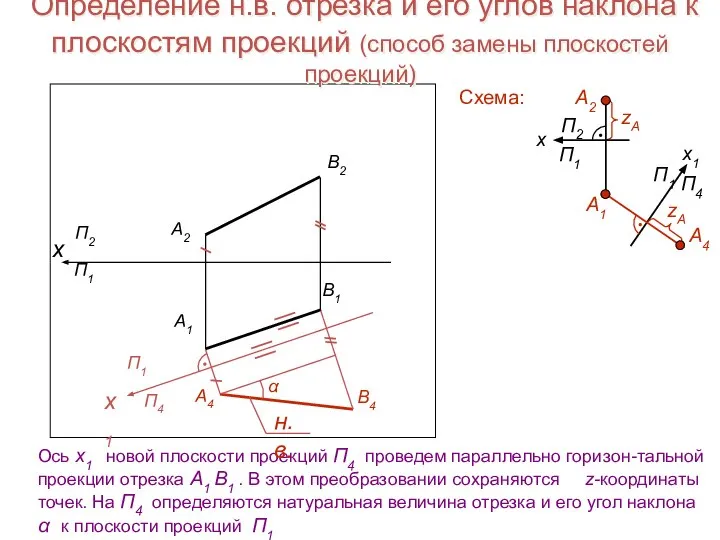
- 17. Определение н.в. отрезка и его углов наклона к плоскостям проекций (способ замены плоскостей проекций) Ось х1
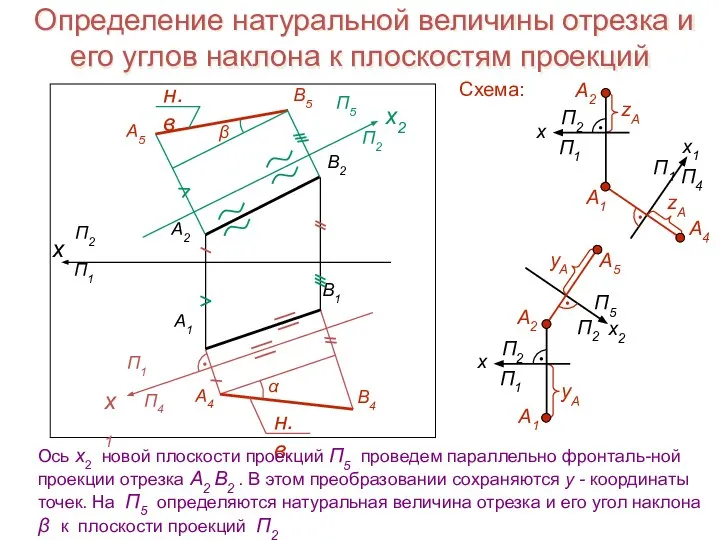
- 18. Определение натуральной величины отрезка и его углов наклона к плоскостям проекций x А1 B1 А2 B2
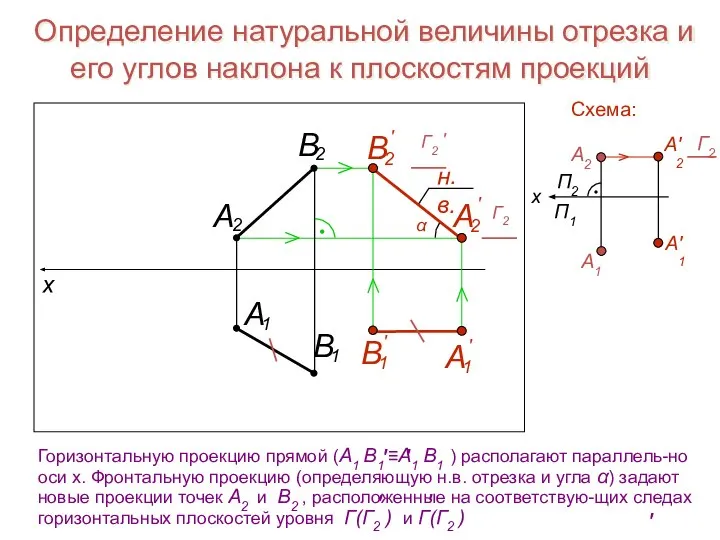
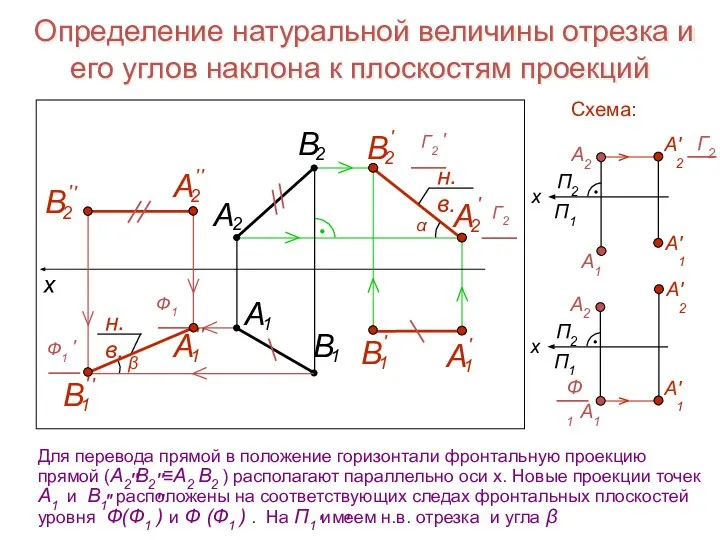
- 19. Определение натуральной величины отрезка и его углов наклона к плоскостям проекций
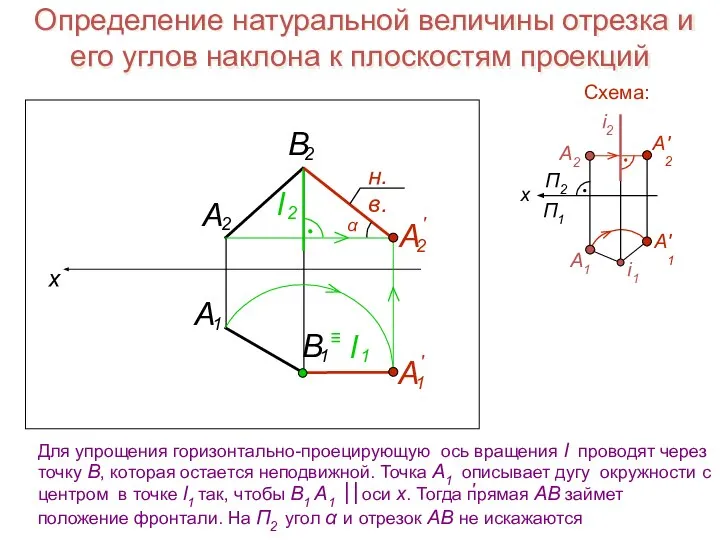
- 20. Определение натуральной величины отрезка и его углов наклона к плоскостям проекций
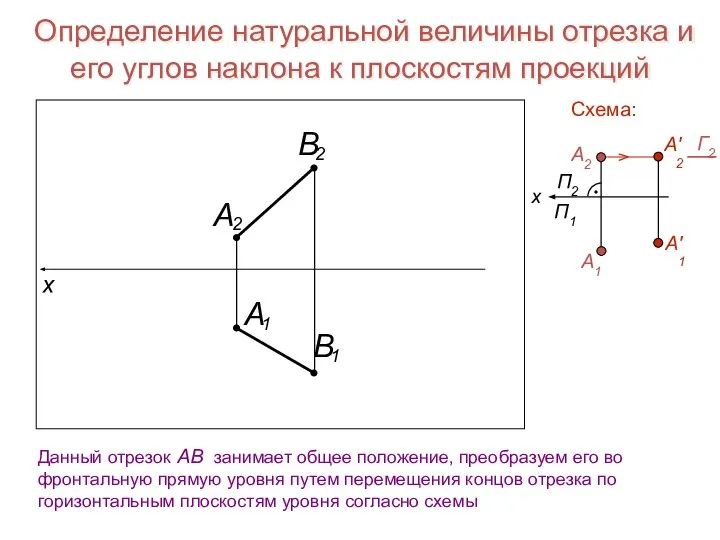
- 21. Определение натуральной величины отрезка и его углов наклона к плоскостям проекций Данный отрезок АВ занимает общее
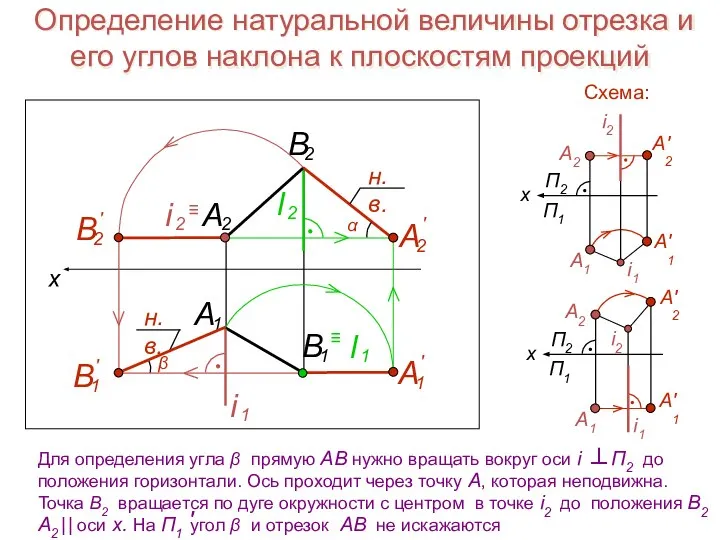
- 22. Определение натуральной величины отрезка и его углов наклона к плоскостям проекций
- 23. Определение натуральной величины отрезка и его углов наклона к плоскостям проекций Схема:
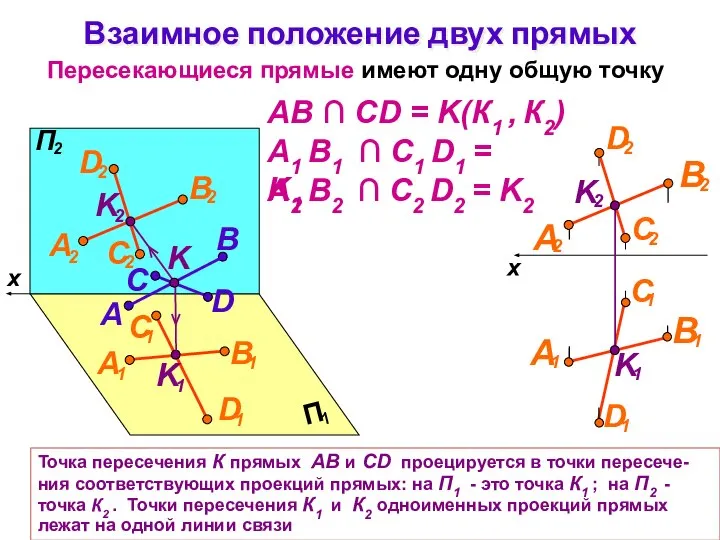
- 24. Взаимное положение двух прямых Пересекающиеся прямые имеют одну общую точку B A D C K x
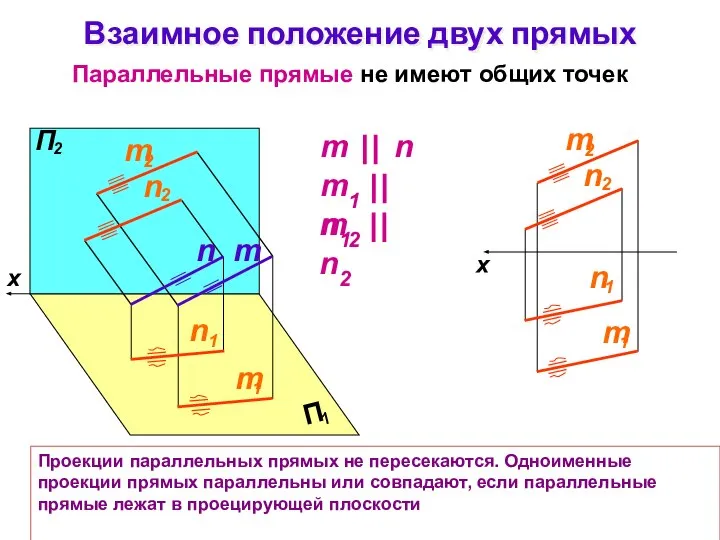
- 25. Взаимное положение двух прямых Параллельные прямые не имеют общих точек Проекции параллельных прямых не пересекаются. Одноименные
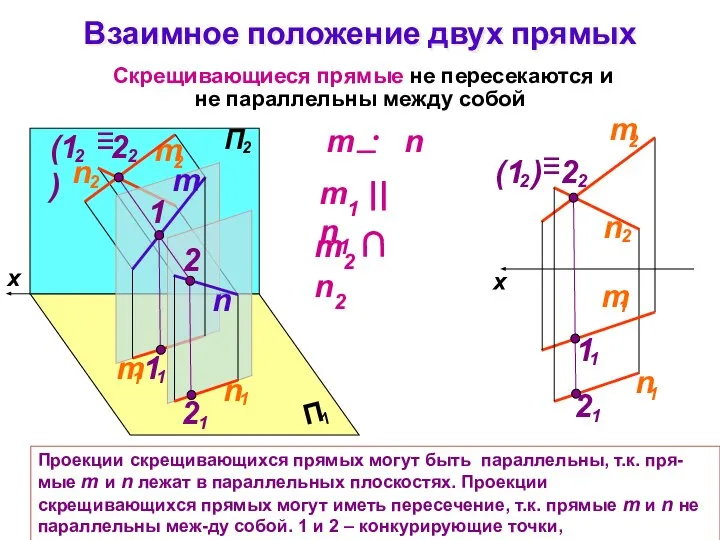
- 26. Взаимное положение двух прямых Скрещивающиеся прямые не пересекаются и не параллельны между собой Проекции скрещивающихся прямых
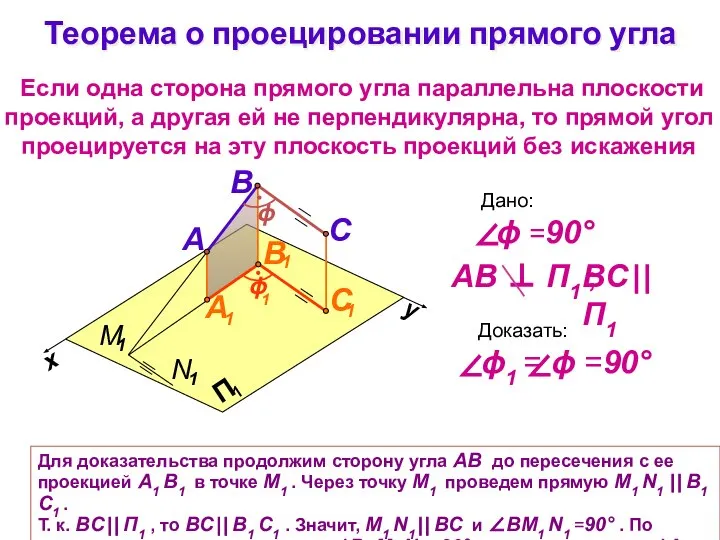
- 27. Теорема о проецировании прямого угла Если одна сторона прямого угла параллельна плоскости проекций, а другая ей
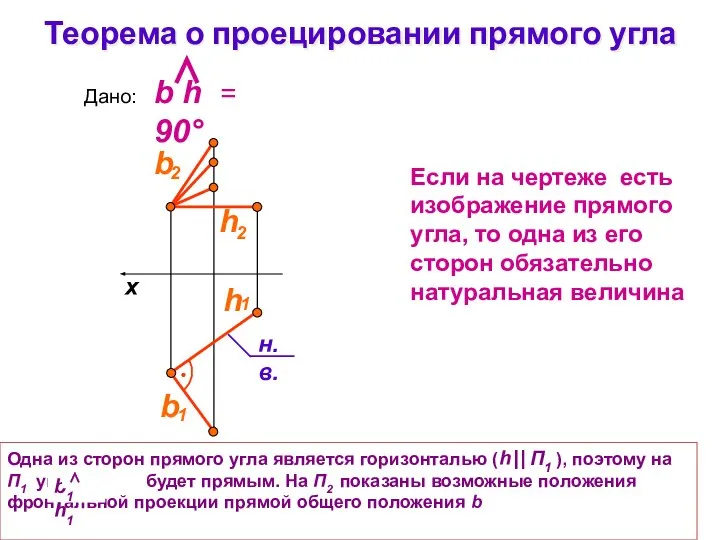
- 28. Теорема о проецировании прямого угла Если на чертеже есть изображение прямого угла, то одна из его
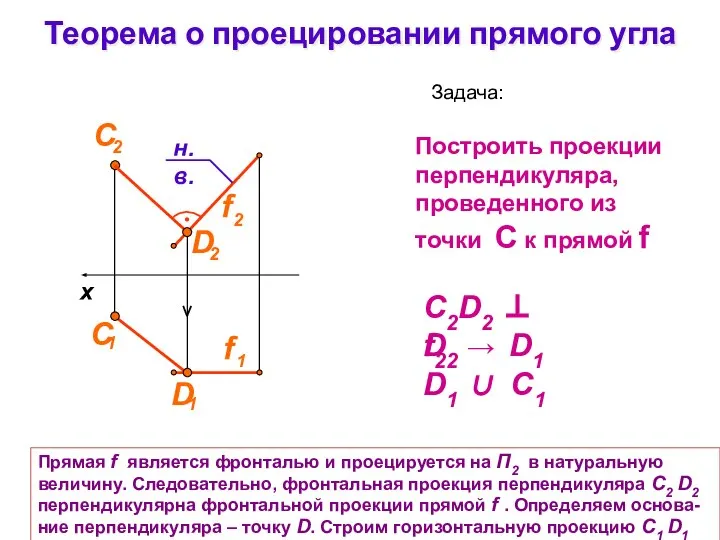
- 29. Теорема о проецировании прямого угла Задача: Построить проекции перпендикуляра, проведенного из точки С к прямой f
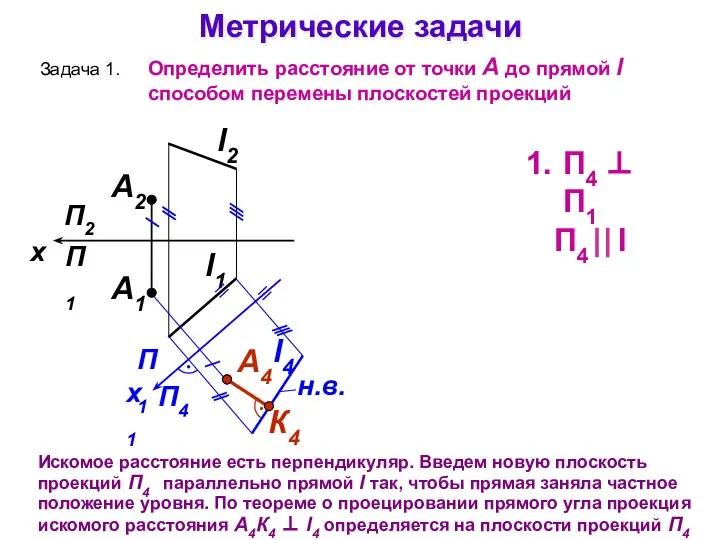
- 30. Метрические задачи Задача 1. Определить расстояние от точки А до прямой l способом перемены плоскостей проекций
- 32. Скачать презентацию


 Абузярова Луиза Ибрагимовна
Абузярова Луиза Ибрагимовна Teatro Colon
Teatro Colon Организация образовательной деятельности в условиях ФГОС для обучающихся с ОВЗ
Организация образовательной деятельности в условиях ФГОС для обучающихся с ОВЗ Прогресс-Гарант
Прогресс-Гарант Мы рады приветствовать вас в группе компаний ПИК
Мы рады приветствовать вас в группе компаний ПИК ВКР: Геодезические работы при строительстве СПГ Портовая
ВКР: Геодезические работы при строительстве СПГ Портовая Детское объединение Юность
Детское объединение Юность Правила дорожного движения для пешехода
Правила дорожного движения для пешехода Эмблема ООН
Эмблема ООН Природные сообщества
Природные сообщества Противодействие утечкам конфиденциальной информации и персональных данных
Противодействие утечкам конфиденциальной информации и персональных данных Мультиспонсорский проект «Междисциплинарный подход в терапии внутренних болезней»
Мультиспонсорский проект «Междисциплинарный подход в терапии внутренних болезней» Типы ВНД. Запольская М. Борзых Ю
Типы ВНД. Запольская М. Борзых Ю Работа выполнена в рамках проекта «Повышение квалификаций различных категорий работников образования и формирование у них базов
Работа выполнена в рамках проекта «Повышение квалификаций различных категорий работников образования и формирование у них базов Олимпиада школьников Ломоносов по психологии
Олимпиада школьников Ломоносов по психологии Презентация на тему Напряжение
Презентация на тему Напряжение Cтивен Р. Кови Принцип-центричное руководство
Cтивен Р. Кови Принцип-центричное руководство Russian presidential academy of the national economy and public admistration noth-west institute of management municipal
Russian presidential academy of the national economy and public admistration noth-west institute of management municipal Шагаа сүзүктери
Шагаа сүзүктери Класификация товаров
Класификация товаров Was machen wir in der Freizeit
Was machen wir in der Freizeit Основы теории конечных автоматов
Основы теории конечных автоматов Наука и полёт фантазии (анализ главы 12 из романа «Затерянный мир»)
Наука и полёт фантазии (анализ главы 12 из романа «Затерянный мир») Воображение и творчество
Воображение и творчество «Тропинка, кочки, копна»
«Тропинка, кочки, копна» Kochaj mnie
Kochaj mnie yfvhyt
yfvhyt Еда и напитки, не выходя из офиса
Еда и напитки, не выходя из офиса