Проецирование плоскости

ПЛАН ЛЕКЦИИ:
Задание и изображение плоскости.
Следы плоскости.
Положение плоскости относительно плоскостей проекций.
Точка и прямая, расположенные в плоскости.
Главные линии плоскости.
Определение углов наклона плоскости к плоскостям проекций.
Взаимное положение прямой и плоскости.
Взаимное расположение двух плоскостей.

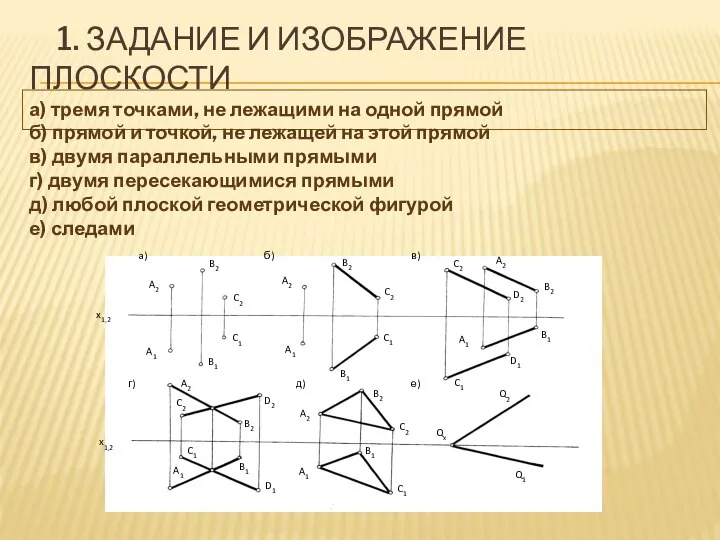
1. ЗАДАНИЕ И ИЗОБРАЖЕНИЕ ПЛОСКОСТИ
а) тремя точками, не лежащими на одной прямой
б) прямой и точкой, не лежащей на этой прямой
в) двумя параллельными прямыми
г) двумя пересекающимися прямыми
д) любой плоской геометрической фигурой
е) следами

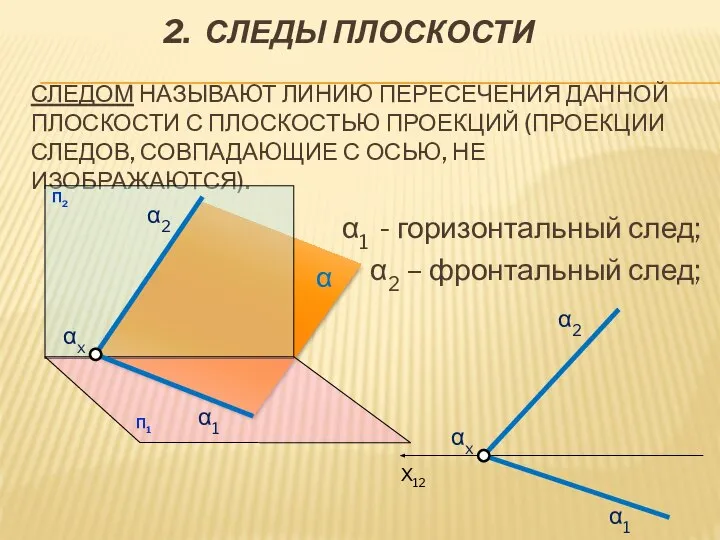
2. СЛЕДЫ ПЛОСКОСТИ
СЛЕДОМ НАЗЫВАЮТ ЛИНИЮ ПЕРЕСЕЧЕНИЯ ДАННОЙ ПЛОСКОСТИ С ПЛОСКОСТЬЮ ПРОЕКЦИЙ (ПРОЕКЦИИ СЛЕДОВ, СОВПАДАЮЩИЕ С ОСЬЮ, НЕ ИЗОБРАЖАЮТСЯ).
α1 - горизонтальный след;
α2 – фронтальный след;
α
α2
α1
α2
α1
αx
αx

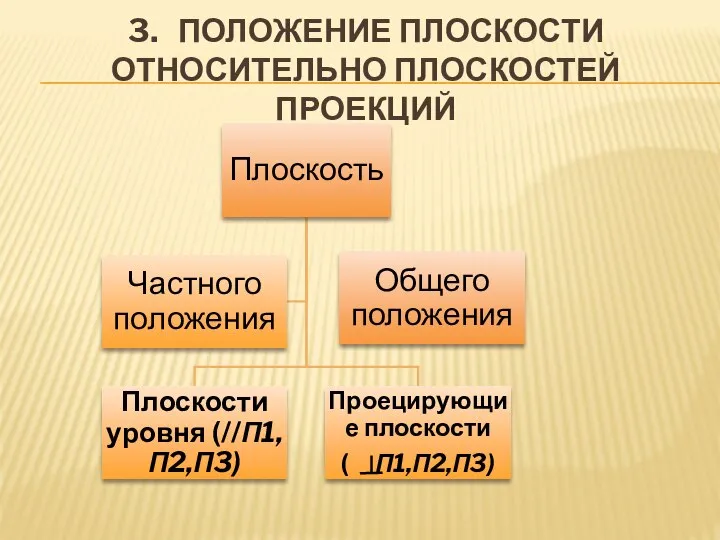
3. ПОЛОЖЕНИЕ ПЛОСКОСТИ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ

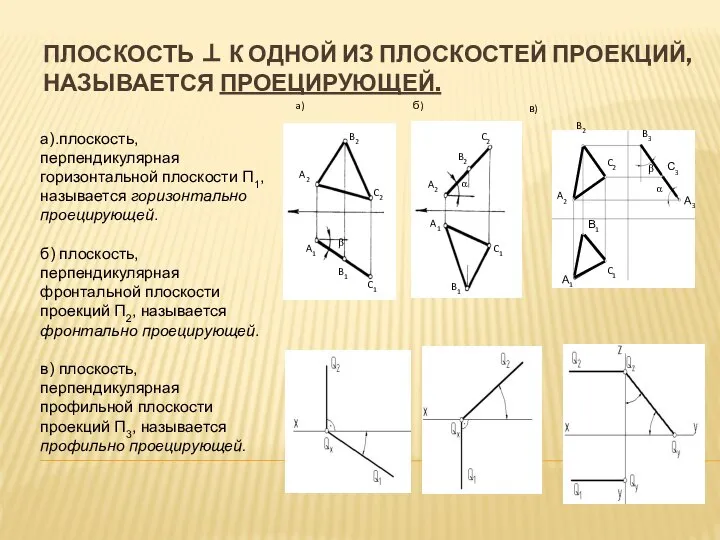
ПЛОСКОСТЬ ⊥ К ОДНОЙ ИЗ ПЛОСКОСТЕЙ ПРОЕКЦИЙ, НАЗЫВАЕТСЯ ПРОЕЦИРУЮЩЕЙ.
a)
б)
в)
а).плоскость, перпендикулярная горизонтальной плоскости П1, называется горизонтально проецирующей.
б) плоскость, перпендикулярная фронтальной плоскости проекций П2, называется фронтально проецирующей.
в) плоскость, перпендикулярная профильной плоскости проекций П3, называется профильно проецирующей.

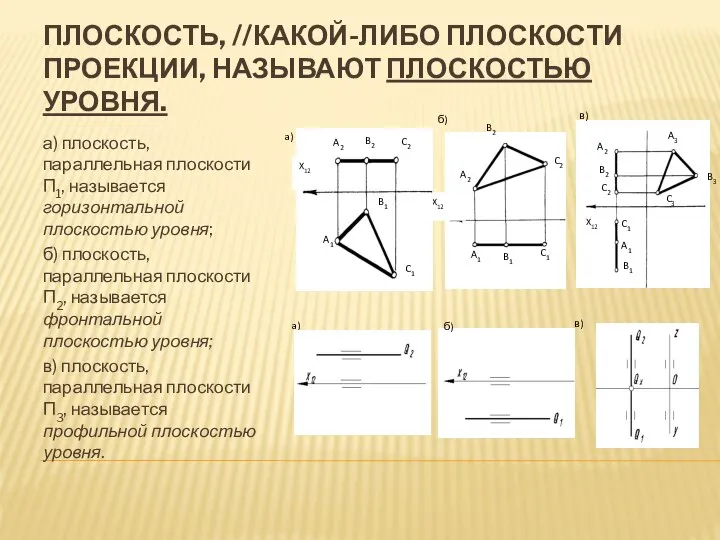
ПЛОСКОСТЬ, //КАКОЙ-ЛИБО ПЛОСКОСТИ ПРОЕКЦИИ, НАЗЫВАЮТ ПЛОСКОСТЬЮ УРОВНЯ.
а) плоскость, параллельная плоскости П1, называется горизонтальной плоскостью уровня;
б) плоскость, параллельная плоскости П2, называется фронтальной плоскостью уровня;
в) плоскость, параллельная плоскости П3, называется профильной плоскостью уровня.
a)
б)
в)

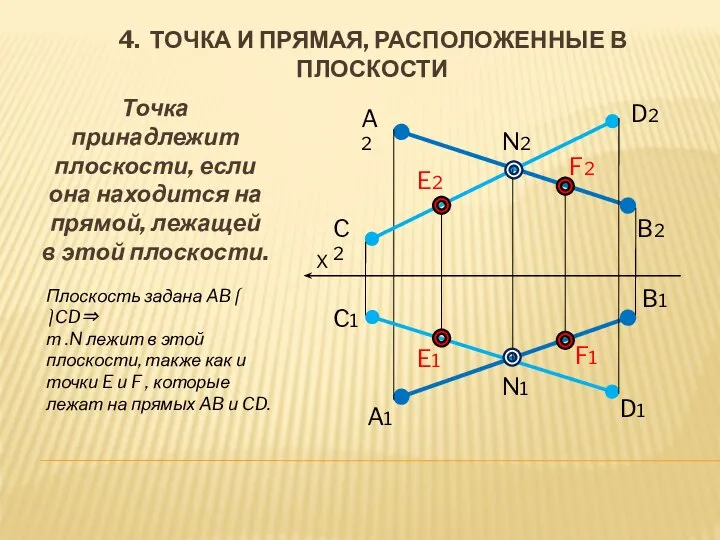
4. ТОЧКА И ПРЯМАЯ, РАСПОЛОЖЕННЫЕ В ПЛОСКОСТИ
Точка принадлежит плоскости, если она находится на прямой, лежащей в этой плоскости.
X
A1
B1
B2
A2
C2
C1
N1
N2
D2
D1
E2
E1
F2
F1
Плоскость задана AB⎧ ⎫CD⇒
т .N лежит в этой
плоскости, также как и точки E и F , которые лежат на прямых AB и CD.

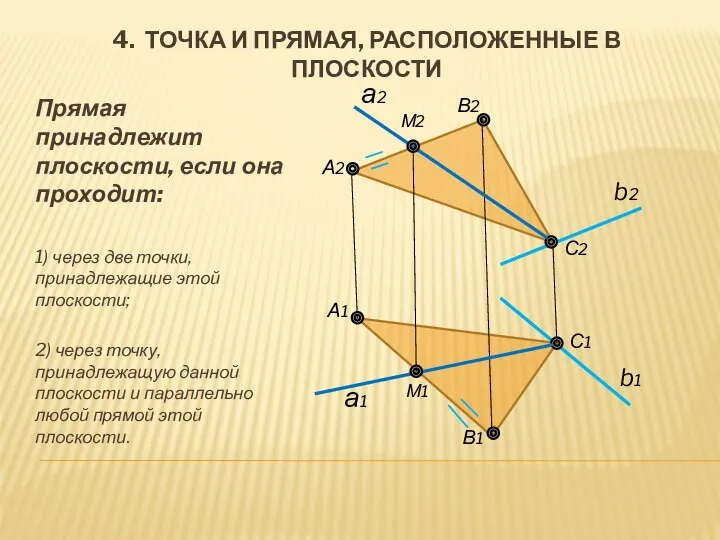
Прямая принадлежит плоскости, если она проходит:
1) через две точки, принадлежащие этой плоскости;
2) через точку, принадлежащую данной плоскости и параллельно любой прямой этой плоскости.
4. ТОЧКА И ПРЯМАЯ, РАСПОЛОЖЕННЫЕ В ПЛОСКОСТИ
А1
А2
В2
В1
С2
С1
М2
М1
а2
а1
b2
b1

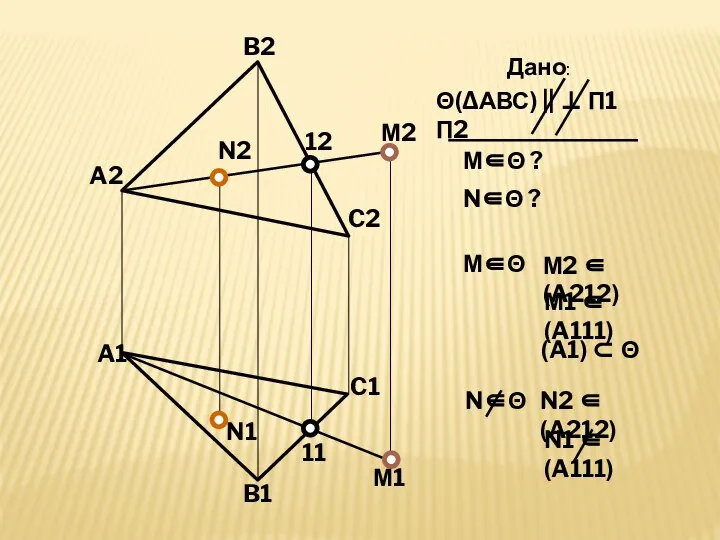
М2
М1
N2
N1
12
11
A2
B2
C2
C1
B1
A1
Дано:
Θ(ΔАВС) || ⊥ П1 П2
М∈Θ ?
N∈Θ ?
М∈Θ
М2 ∈(A212)
М1 ∈(A111)
(A1) ⊂ Θ
N∈Θ
N2 ∈(A212)
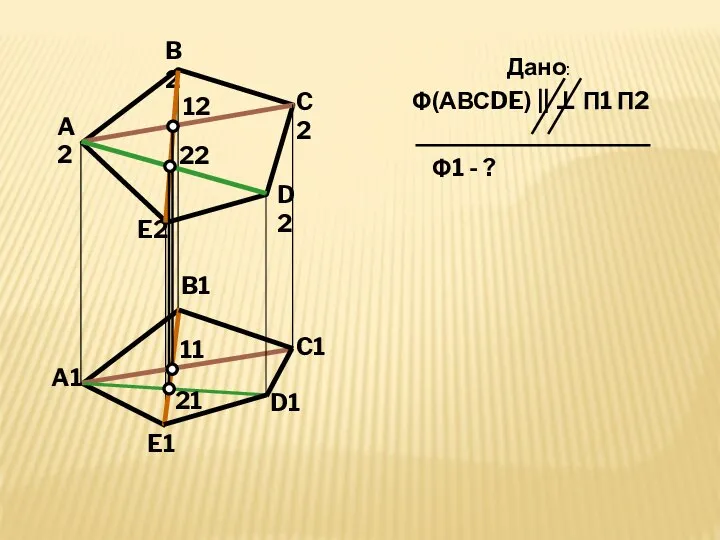
N1 ∈(A111)

A2
B2
C1
D2
E2
A1
B1
E1
Дано:
Φ(АВСDE) || ⊥ П1 П2
Φ1 - ?
C2
D1
12
11
22
21

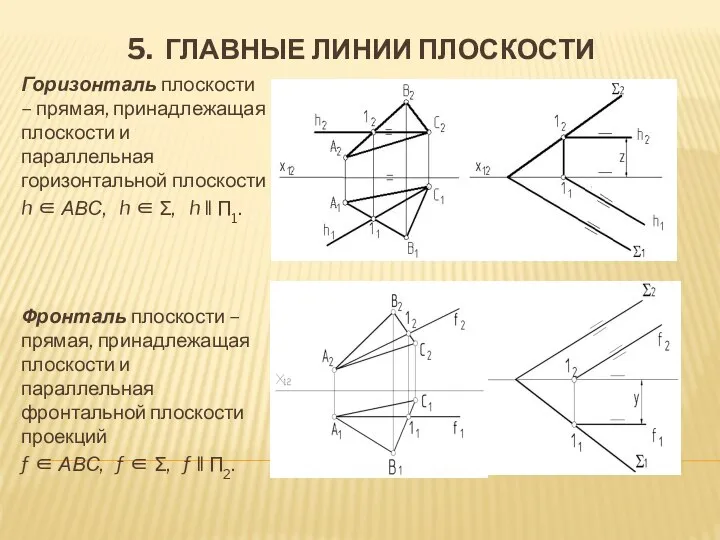
5. ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ
Горизонталь плоскости – прямая, принадлежащая плоскости и параллельная горизонтальной плоскости
h ∈ АВС, h ∈ Σ, h ‖ П1.
Фронталь плоскости – прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций
ƒ ∈ АВС, ƒ ∈ Σ, ƒ ‖ П2.

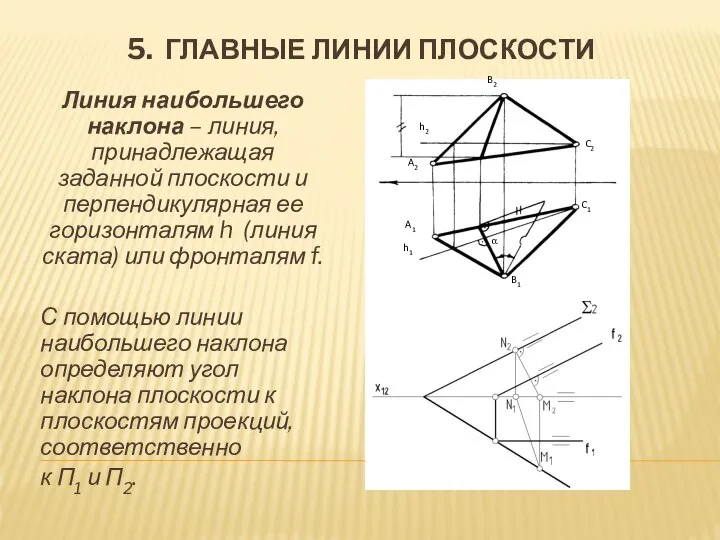
5. ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИ
Линия наибольшего наклона – линия, принадлежащая заданной плоскости и перпендикулярная ее горизонталям h (линия ската) или фронталям f.
С помощью линии наибольшего наклона определяют угол наклона плоскости к плоскостям проекций, соответственно
к П1 и П2.

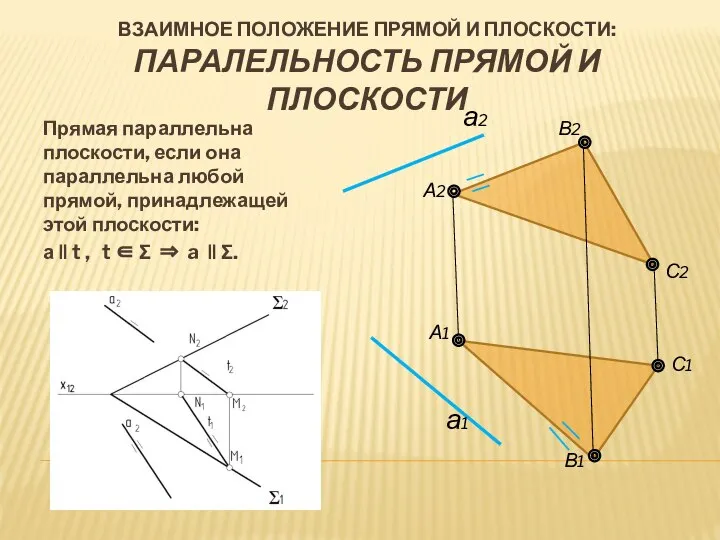
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ:
ПАРАЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Прямая параллельна плоскости, если она параллельна любой прямой, принадлежащей этой плоскости:
а ‖ t , t ∈ Σ ⇒ a ‖ Σ.
А1
А2
В2
В1
С2
С1
а2
а1

ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ:
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Если плоскость задана следами, то горизонталью и фронталью плоскости являются ее пересекающиеся следы
а1 ⊥ Σ1, а2 ⊥ Σ2,
Σ1 Ⴖ Σ2 ⇒ а ⊥ Σ.
В качестве пересекающихся прямых на плоскости выбирают горизонталь h и фронталь ƒ.
В этом случае можно воспользоваться свойствами проекций прямого угла:
a ⊥ h, a ⊥ ƒ, h Ⴖ ƒ,
h ⊂ Σ, ƒ ⊂ Σ ⇒ а ⊥ Σ.
При этом прямые углы между прямой а и прямыми h и ƒ на соответствующие плоскости проекций спроецируются в натуральную величину:
а1 ⊥ h1, а2 ⊥ ƒ2.
Прямая перпендикулярна плоскости , если она перпендикулярна двумя пересекающимся прямым, лежащим в этой плоскости.

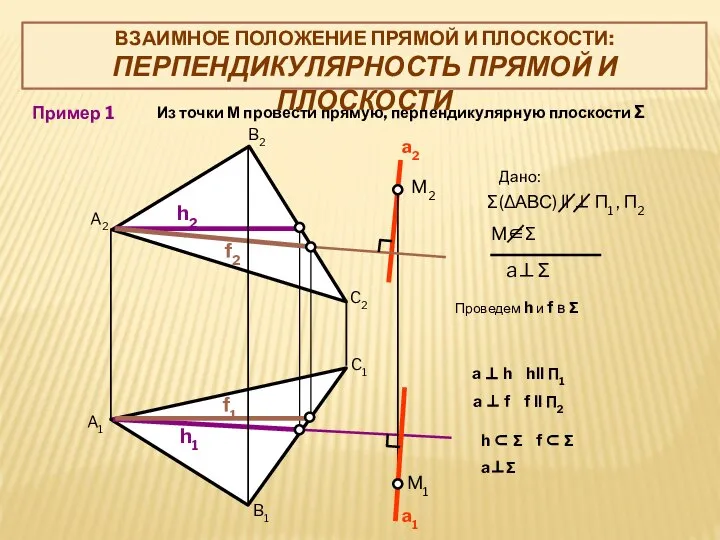
a⊥Σ
Пример 1
Из точки М провести прямую, перпендикулярную плоскости Σ
M2
M1
a1
a2
A2
B2
C2
C1
B1
A1
h2
h1
f1
f2
Дано:
M∈Σ
Проведем h и f в Σ
a ⊥ h hll П1
a ⊥ f f ll П2
h ⊂ Σ f ⊂ Σ
a⊥Σ
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ:
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ

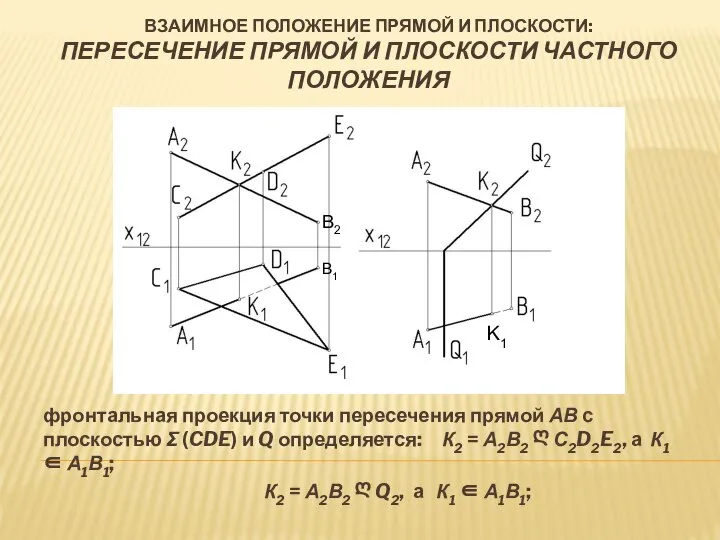
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ:
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ
фронтальная проекция точки пересечения прямой АВ с плоскостью Σ (CDE) и Q определяется: К2 = А2В2 Ⴖ С2D2E2, а К1 ∈ А1В1;
К2 = А2В2 Ⴖ Q2, а К1 ∈ А1В1;

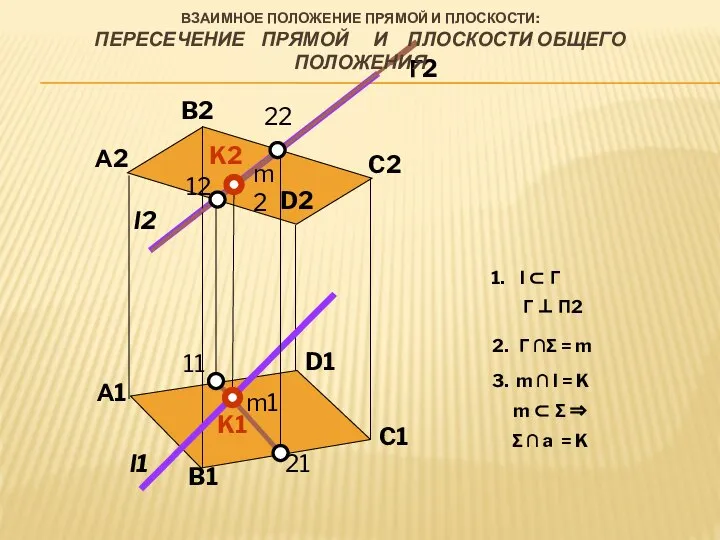
А2
B2
C2
D2
D1
C1
B1
А1
l2
l1
K1
K2
Г2
m2
m1
12
22
11
21
1. l ⊂ Г
Г ⊥ П2
2. Г ∩Σ = m
3. m ∩ l = K
m ⊂ Σ ⇒
Σ ∩ a = K
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ:
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ

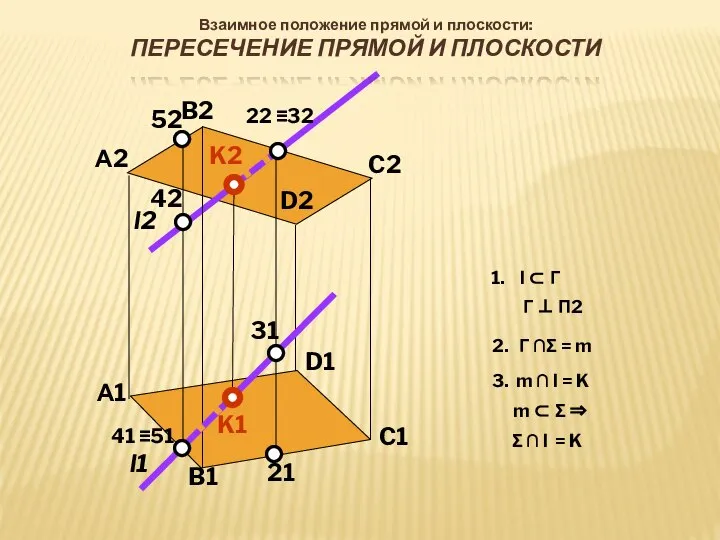
А2
B2
C2
D2
D1
C1
B1
А1
l2
l1
K1
K2
22 ≡32
31
21
41 ≡51
52
42
1. l ⊂ Г
Г ⊥ П2
2. Г ∩Σ = m
3. m ∩ l = K
m ⊂ Σ ⇒
Σ ∩ l = K
Взаимное положение прямой и плоскости:
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ

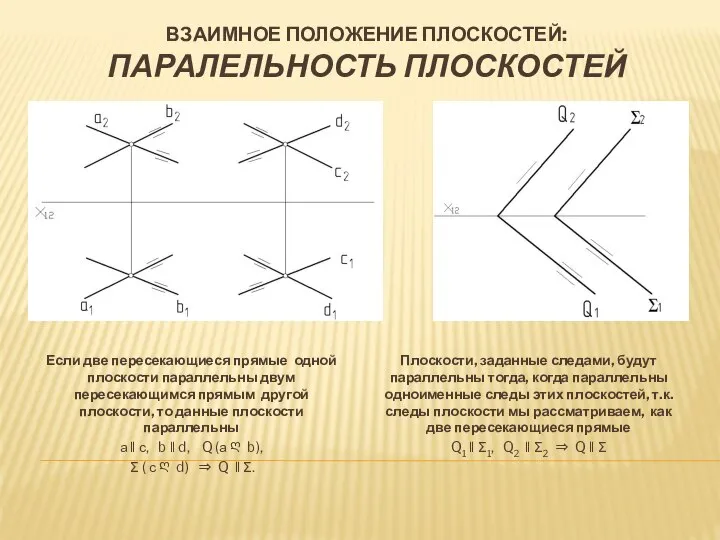
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ:
ПАРАЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ
Плоскости, заданные следами, будут параллельны тогда, когда параллельны одноименные следы этих плоскостей, т.к. следы плоскости мы рассматриваем, как две пересекающиеся прямые
Q1 ‖ Σ1, Q2 ‖ Σ2 ⇒ Q ‖ Σ
Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то данные плоскости параллельны
а ‖ с, b ‖ d, Q (а Ⴖ b),
Σ ( с Ⴖ d) ⇒ Q ‖ Σ.

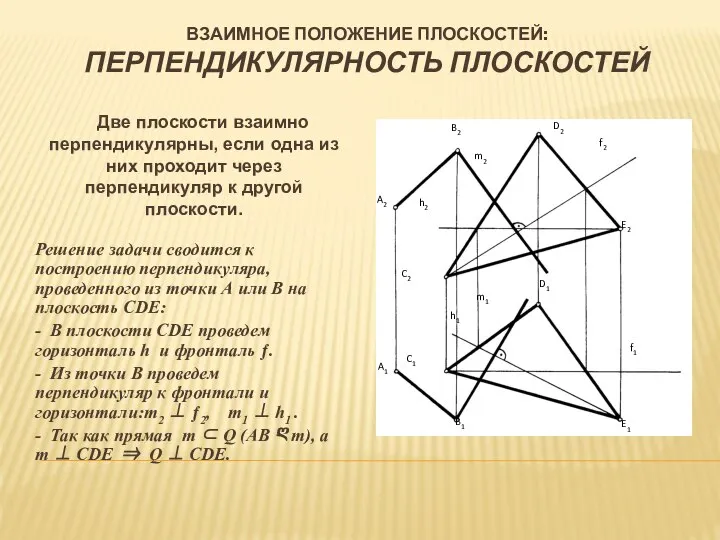
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ:
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
Решение задачи сводится к построению перпендикуляра, проведенного из точки А или В на плоскость CDE:
- В плоскости CDE проведем горизонталь h и фронталь ƒ.
- Из точки В проведем перпендикуляр к фронтали и горизонтали:m2 ⊥ ƒ2, m1 ⊥ h1 .
- Так как прямая m ⊂ Q (AB Ⴖ m), a m ⊥ CDE ⇒ Q ⊥ CDE.
Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой плоскости.

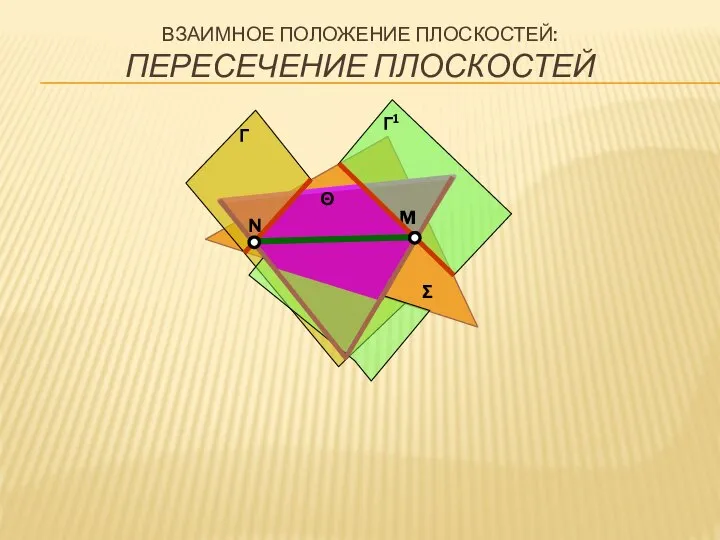
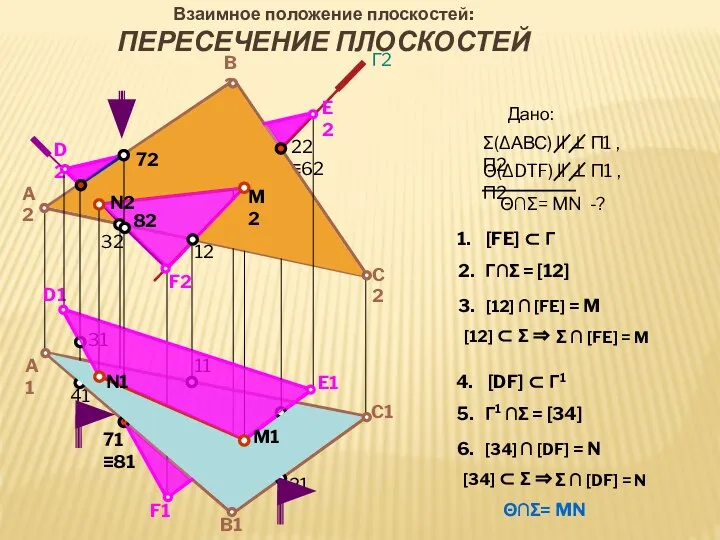
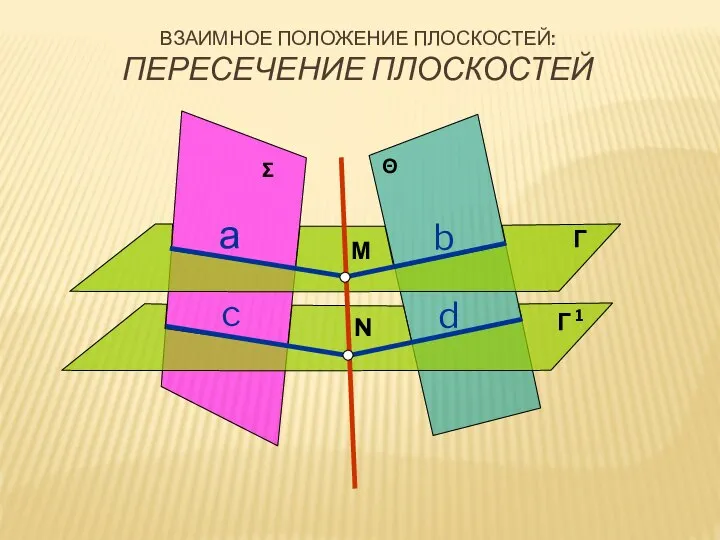
M
N
Г
Θ
Г1
Σ
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ:
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ

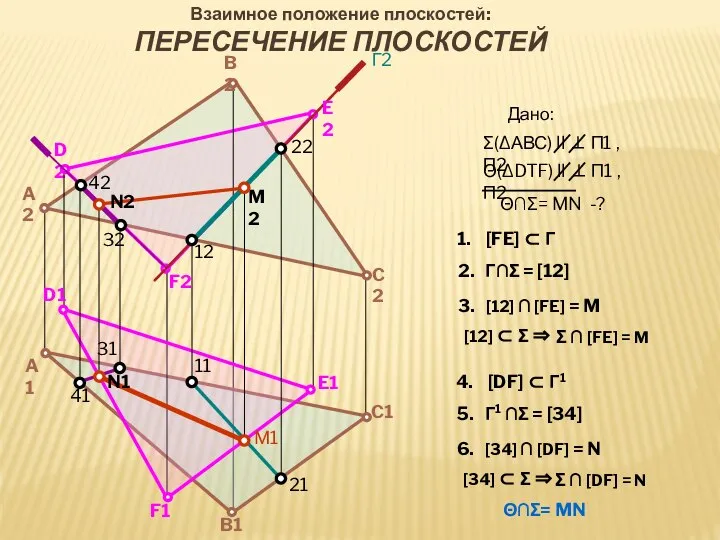
D2
21
22
F1
A2
B2
C2
C1
B1
A1
F2
D1
E1
Г2
E2
12
11
M1
M2
32
31
42
41
1. [FE] ⊂ Г
2. Г∩Σ = [12]
3. [12] ∩ [FE] = M [12] ⊂ Σ ⇒
Σ ∩ [FE] = M
Дано:
Θ∩Σ= MN -?
4. [DF] ⊂ Г1
5. Г1 ∩Σ = [34]
6. [34] ∩ [DF] = N
[34] ⊂ Σ ⇒
Σ ∩ [DF] = N
Θ∩Σ= MN
N1
N2
Взаимное положение плоскостей:
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ

21
41
D2
22 ≡62
F1
A2
B2
C2
C1
B1
A1
F2
D1
E1
Г2
E2
12
11
32
31
42=52
1. [FE] ⊂ Г
2. Г∩Σ = [12]
3. [12] ∩ [FE] = M
[12] ⊂ Σ ⇒
Σ ∩ [FE] = M
Дано:
Θ∩Σ= MN -?
4. [DF] ⊂ Г1
5. Г1 ∩Σ = [34]
6. [34] ∩ [DF] = N
[34] ⊂ Σ ⇒
Σ ∩ [DF] = N
Θ∩Σ= MN
61
N2
M2
71 ≡81
72
82
M1
N1
Взаимное положение плоскостей:
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ

М
N
Σ
Θ
Г
Г 1
а
d
b
c
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ:
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ