Содержание
- 2. Проецирование отрезка прямой линии на 3 плоскости проекций. ПЛАН: Определение прямой в пространстве. Проецирование прямой общего
- 3. Что такое отрезок? Отрезком называется - прямая ограниченная двумя точками
- 4. Прямая общего положения Прямая общего положения - это прямая не параллельная и не перпендикулярная ни одной
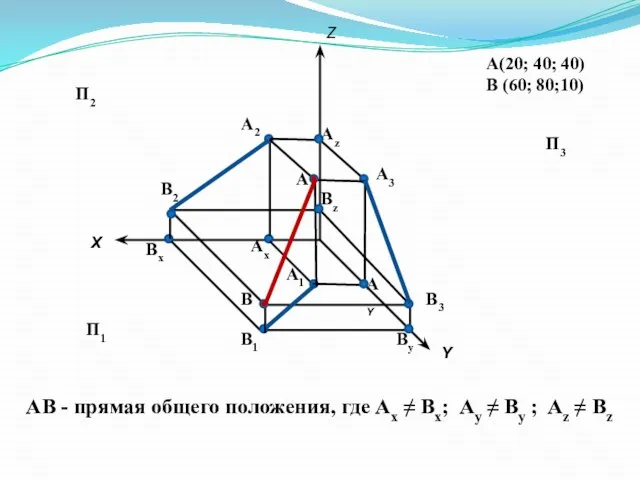
- 5. А(20; 40; 40) В (60; 80;10) Х Y Z А2 А1 А3 А В2 В1 В3
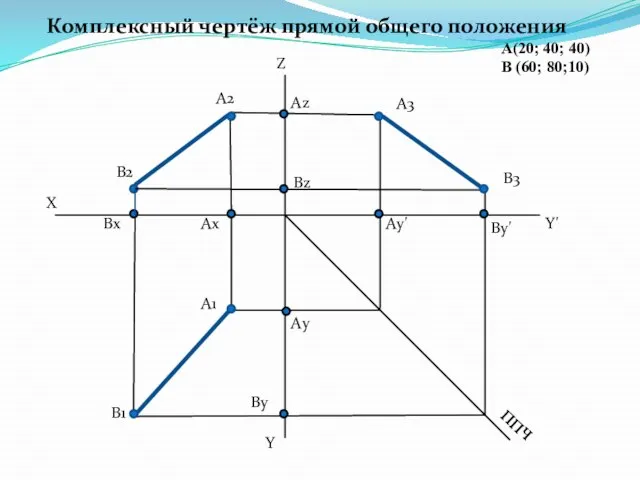
- 6. А(20; 40; 40) В (60; 80;10) Ах Аz Аy' Аy А3 А2 А1 Bх By By'
- 7. Прямые уровня Прямая параллельная одной из плоскостей проекций
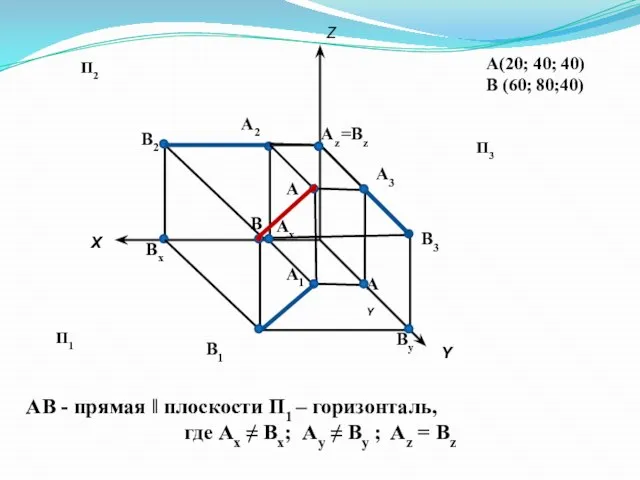
- 8. А(20; 40; 40) В (60; 80;40) Х Y Z А2 А1 А3 А В2 В1 В3
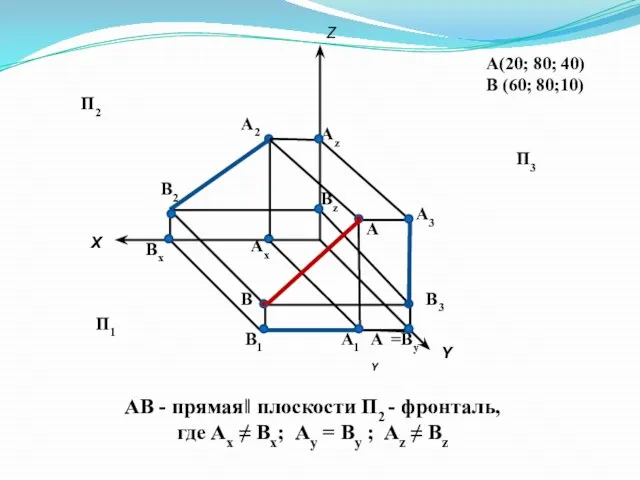
- 9. А(20; 80; 40) В (60; 80;10) Х Y Z А2 А1 А3 А В2 В1 В3
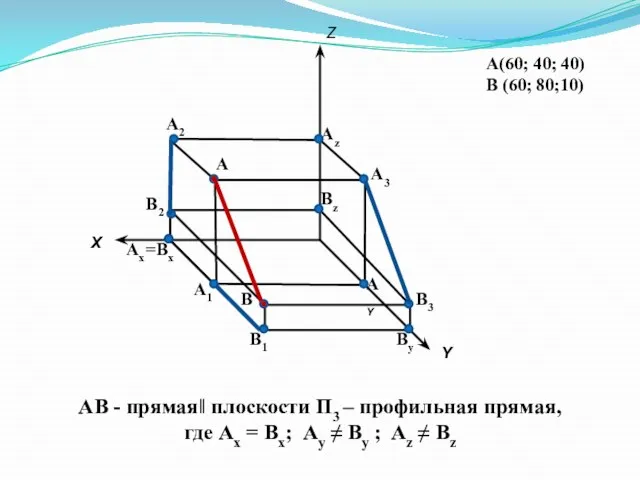
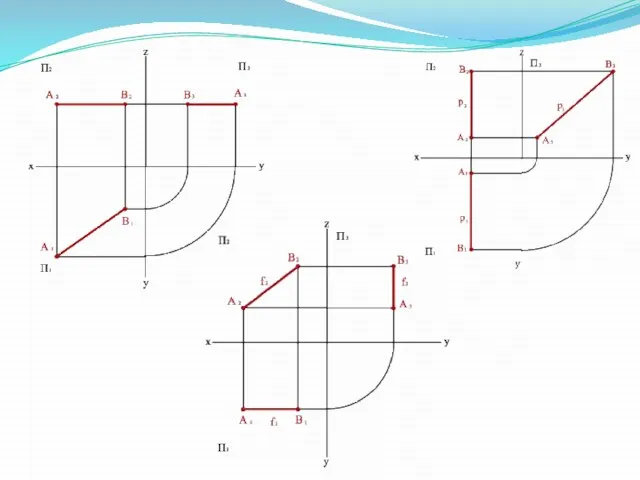
- 10. А(60; 40; 40) В (60; 80;10) Х Y Z А2 А1 А3 А В2 В1 В3
- 12. Проецирующие прямые Прямая перпендикулярная одной из плоскостей проекций
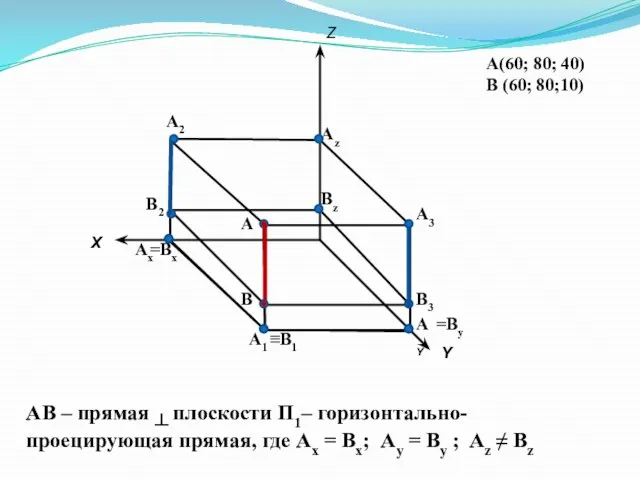
- 13. А(60; 80; 40) В (60; 80;10) Х Y Z А2 А1 А3 А В2 ≡В1 В3
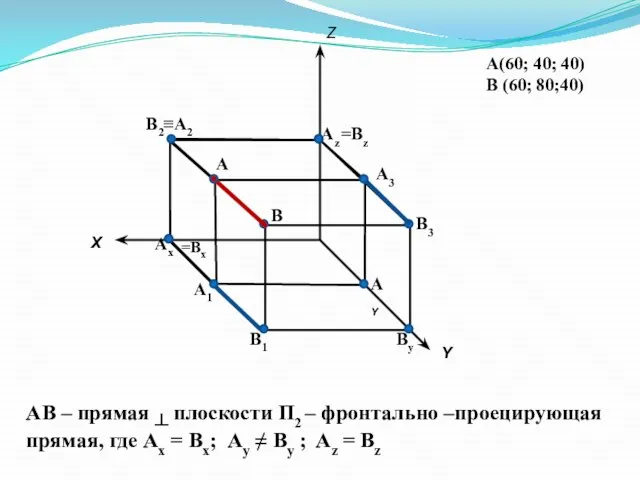
- 14. А(60; 40; 40) В (60; 80;40) Х Y Z А2 А1 А3 А В2≡ В1 В3
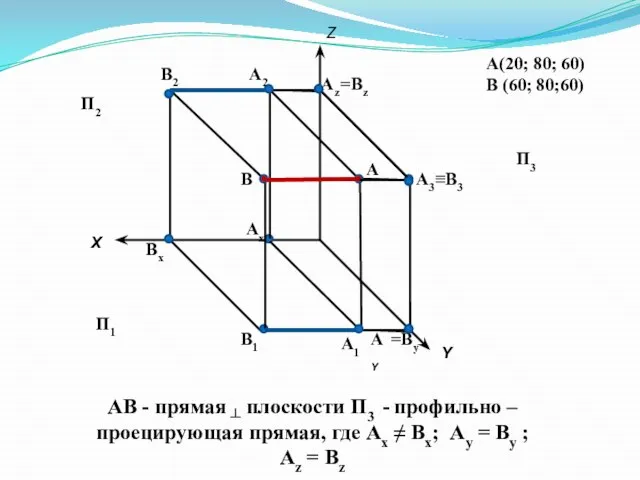
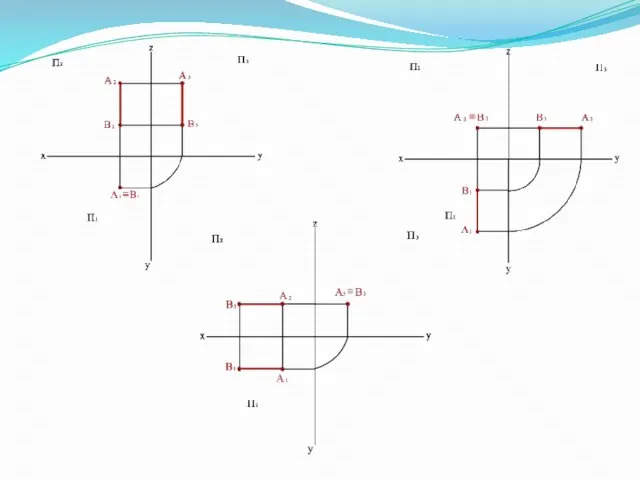
- 15. А(20; 80; 60) В (60; 80;60) Х Y Z А2 А1 А3 А В2 В1 ≡В3
- 17. Следы прямой Следом прямой линии называется точка пересечения прямой с плоскостью проекций.
- 19. Скачать презентацию






 Газификация Волгоградской области
Газификация Волгоградской области Пространство для партнерства
Пространство для партнерства Конституция ДНР
Конституция ДНР Строим…Модернизируем…
Строим…Модернизируем… ШАГ ВТОРОЙ Спонсирование и построение группы
ШАГ ВТОРОЙ Спонсирование и построение группы Суп. Ингредиенты
Суп. Ингредиенты Нагорная проповедь
Нагорная проповедь Возможные причины моббинга
Возможные причины моббинга ДИНАМИКА ТВЕРДОГО ТЕЛА
ДИНАМИКА ТВЕРДОГО ТЕЛА Обеспечение качества подготовки выпускных квалификационных работ в условиях дистанционного обучения
Обеспечение качества подготовки выпускных квалификационных работ в условиях дистанционного обучения Работа текучих вод, ледников и ветра
Работа текучих вод, ледников и ветра Компьютерные вирусы (8 класс)
Компьютерные вирусы (8 класс) Ах, карнавал! Удивительный мир!
Ах, карнавал! Удивительный мир! Джеймс Олдридж
Джеймс Олдридж Презентация на тему Босния и Герцеговина
Презентация на тему Босния и Герцеговина  ШКОЛА №4
ШКОЛА №4 Квадрат суммы и квадрат разности
Квадрат суммы и квадрат разности Презентация на тему Действия с рациональными числами (6 класс)
Презентация на тему Действия с рациональными числами (6 класс)  Невербальное общение
Невербальное общение Алексей Николаевич Апухтин
Алексей Николаевич Апухтин АКАДЕМИЯ
АКАДЕМИЯ Применение инновационной предпринимательской стратегии BMW
Применение инновационной предпринимательской стратегии BMW Права школьника
Права школьника Биржа. Ценные бумаги. Отличие облигации от банковского депозита
Биржа. Ценные бумаги. Отличие облигации от банковского депозита Обособление
Обособление Презентация на тему Советская музыка
Презентация на тему Советская музыка Стилистические особенности сонетов Шекспира
Стилистические особенности сонетов Шекспира ХХ век
ХХ век