Содержание
- 2. Цели профильного обучения: предоставить школьникам возможность профильно изучать отдельные дисциплины, программы полного общего образования; Подготовить обучающихся
- 3. Задачи: Разработать программы профильного обучения; Обеспечить кадровую подготовку к профильному обучению; Учитывать соответствие программ требованиям вузов;
- 4. Профильные классы: Физико-математический и социально-гуманитарный. Средства: МТБ школы недостаточная (техническое оснащение кабинетов, оборудование) учебно – методическое
- 5. Учебно – методическое оснащение профильного обучения Физико-математический профиль Социально-гуманитарный профиль
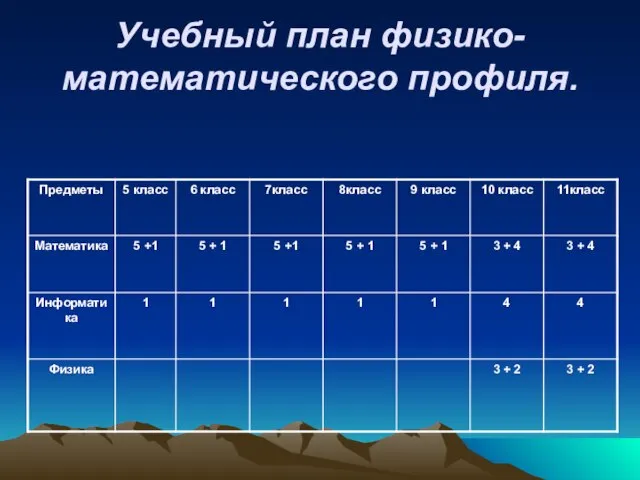
- 6. Учебный план физико-математического профиля.
- 7. Учебный план социально-гуманитарного профиля.
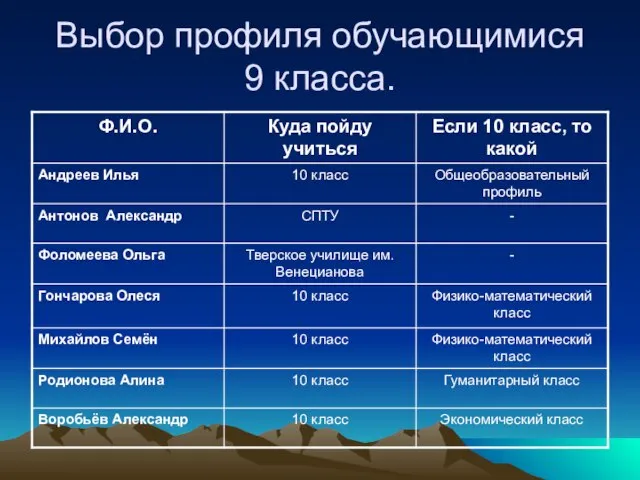
- 8. Выбор профиля обучающимися 9 класса.
- 9. Диагностика выбора профиля в 2006-2007 учебном году. Общеобразовательный класс -41 % Гуманитарный класс-6 % Физико-математический класс-19%
- 10. Поступление в вузы и колледжи. ( физико-математический профиль выпуск 2005-06 учебный год) Технические вузы: 63 %
- 12. Занимательные задачи ученицы 5а класса УСОШ №2 им. Сергея Ступакова Григорьевой Виолетты №1Дедушка и внучка Сколько
- 13. Занимательные задачи ученицы 5а класса УСОШ №2 им. Сергея Ступакова Григорьевой Виолетты №3.Трюк клоуна. Клоунам, имена
- 14. Доклад на тему: «Архимед» ученика 5а класса УСОШ№2 им. Сергея Ступакова Мухи Николая Архимед – великий
- 15. Архимед- инженерный гений. При осаде Сиракуз, богатого торгового города на острове Сицилия, воины римского консула Марцелла
- 16. Архимед- инженерный гений. В «Истории Марцелла» Плутарх описывает ужас, царивший в рядах римских воинов: «Как только
- 17. Архимед - математик Огромен вклад Архимеда и в развитие математики. Спираль Архимеда, описываемая точкой, двигающейся по
- 18. Архимед - математик Учёный вычислил отношение длины окружности к диаметру (число пи). Большую роль в развитии
- 19. Доклад на тему: «Цифры» ученика 5 класса УСОШ №2 им. Сергея Ступакова Тарасова Александра Немало различных
- 20. Арабские цифры Эта система была введена в Европе примерно в 1120 году английским учёным – путешественником
- 21. Римские цифры I – 1; II – 2; V – 5; X – 10;L – 50;
- 22. Римские цифры В настоящее время римские цифры обычно применяют при нумерации глав и разделов книг, месяцев,
- 23. Доклад на тему: «Цифры и числа» учениц 5в класса УСОШ №2 им. Сергея Ступакова Саруханян Нарине
- 24. Римские цифры Если вы хотите записывать римские числа так, чтобы они полностью соответствовали пока ещё не
- 25. Из истории цифр Время изменило внешний облик цифр. Если в XII веке цифры «губар», применявшиеся в
- 26. Из истории цифр Начиная с XIV (14) века? Когда в Европе уже было развито книгопечатание, многие
- 27. Из истории цифр Теперь труднее спутать, скажем, 2 и 5. Правда, это нововведение широко не привилось.
- 28. Из истории цифр Здесь в написании цифр участвуют уже 9 отрезков. Цифры предназначены для электронной машины,
- 29. Занимательные задачи ученицы 5а класса им. Сергея Ступакова Болбат Алёны. 1.Головы и ноги. На лугу паслись
- 30. Занимательные задачи 2. Без гирь. Вам принесли на дом 10 кг сливочного масла. Вы желаете купить
- 31. Занимательные задачи 4. Тысяча. Можете л вы число 1000 выразить восемью восьмёрками? (Кроме цифр, разрешается пользоваться
- 32. Доклад на тему: «Арифметика» ученицы 5а класса УСОШ №2 имени Сергея Ступакова Денисовой Анастасии. С глубокой
- 33. Арифметика К 3 в. до н.э. установилась и другая форма обозначения чисел – иероглифическая. При записи
- 34. Арифметика Издавна в Китае были известны дроби. Некоторые имели даже свои названия. Половина называлась «бань», треть
- 35. Арифметика Отрицательные числа назывались «фу», а положительные «чжен». Постепенно числа «фу» стали истолковывать как долг, недостаток.
- 36. Занимательные задачи 1. В школьный портфель помещается не более четырёх взрослых ежей. Сколько таких портфелей нужно,
- 38. Скачать презентацию

































 МОУ «Журавская СОШ»
МОУ «Журавская СОШ» Мастер-класс по теме кофейная акварель
Мастер-класс по теме кофейная акварель Аннуитеты. Классификация аннуитетов
Аннуитеты. Классификация аннуитетов Презентация на тему Размножение и развитие животных (3 класс)
Презентация на тему Размножение и развитие животных (3 класс)  Семь смертных грехов в христианстве
Семь смертных грехов в христианстве Интерактивная игра типа Лабиринт Падежи
Интерактивная игра типа Лабиринт Падежи Когнитивно поведенческая терапия
Когнитивно поведенческая терапия Повышение информационно-коммуникационной компетентности педагогов
Повышение информационно-коммуникационной компетентности педагогов Роль инновационной образовательной программы в развитии социального партнерства
Роль инновационной образовательной программы в развитии социального партнерства  prezentatsiya-po-literature-emrachyov-illyustrator-basen-iakrylova-5-klass (2)
prezentatsiya-po-literature-emrachyov-illyustrator-basen-iakrylova-5-klass (2) Ащық сабақ. 27,11,2020
Ащық сабақ. 27,11,2020 Новое в содержании образовательных программ по предмету «Физическая культура» в соответствии с ФГОС второго поколения
Новое в содержании образовательных программ по предмету «Физическая культура» в соответствии с ФГОС второго поколения Подгузники Kidy
Подгузники Kidy День 3. Финансы. Накопление. Управление деньгами
День 3. Финансы. Накопление. Управление деньгами Бытовые нагревательные приборы и светильники: принцип действия и назначение. 8 класс
Бытовые нагревательные приборы и светильники: принцип действия и назначение. 8 класс Каталог. Фитиль ватный ТУ 8195-023-44881728-2016. Предназначен для парения, для подачи испаряемой жидкости к испарителю
Каталог. Фитиль ватный ТУ 8195-023-44881728-2016. Предназначен для парения, для подачи испаряемой жидкости к испарителю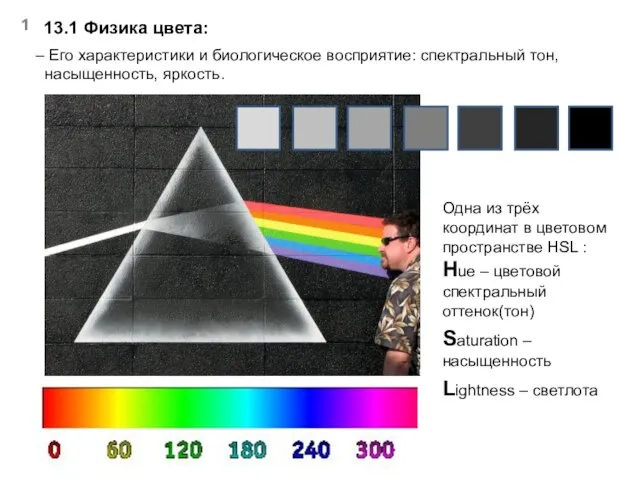 Физика цвета
Физика цвета Действительный член Ассоциации Международных Автомобильных Перевозчиков (АСМАП)
Действительный член Ассоциации Международных Автомобильных Перевозчиков (АСМАП) Презентация на тему Документы, предоставляемые при таможенном декларировании, их виды, примеры, оформление, применение
Презентация на тему Документы, предоставляемые при таможенном декларировании, их виды, примеры, оформление, применение  Публичный отчет МАОУ СОШ № 70
Публичный отчет МАОУ СОШ № 70 Музей боевой славы (Иркутск)
Музей боевой славы (Иркутск) Генераторные установки
Генераторные установки На фоне размещайте изображение
На фоне размещайте изображение Летняя практика. Зарисовки растений
Летняя практика. Зарисовки растений ТЕСТИРОВАНИЕ
ТЕСТИРОВАНИЕ Презентация на тему Периферическая нервная система
Презентация на тему Периферическая нервная система Презентация на тему о зимних Сочинских играх
Презентация на тему о зимних Сочинских играх Liguisan® A
Liguisan® A