Курс лекций по теоретической механике

Лекция 4.
Плоские фермы. Методы расчета. Метод вырезания узлов. Метод Риттера. Понятие о линиях влияния опорных реакций и усилий.
Равновесие сочлененных тел.
Условие равновесия рычага.
Условие устойчивости тела на опрокидывание.
Кинематический способ определения реакций (принцип возможных перемещений).

Лекция 4
Плоские фермы – Геометрически неизменяемые стержневые конструкции, стержни которых лежат в одной плоскости.
Узлы фермы – точки, в которых сходятся оси стержней (опорные узлы – узлы, которыми ферма опирается на основание).
Верхний и нижний пояса – стержни, образующие верхний и нижний контуры.
Стойки – вертикальные стержни.
Раскосы – наклонные стержни.
Пролет фермы – расстояние между опорными узлами (l).
Длина панели – расстояние между стойками (d).
A
B
h
l
d
Методы расчета. Для расчета усилий, возникающих в стержнях ферм,
используются метод вырезания узлов и метод сквозных сечений (метод Риттера).
Основные допущения, принимаемые при расчете ферм:
Все узлы соединения стержней считаются идеальными шарнирами, не
препятствующими взаимному повороту стержней. Узлы в металлических фермах,
в которых стержни соединяются при помощи фасонных листов и заклепок, также
рассматриваются как шарнирные, поскольку при нагрузке они допускают малые
упругие деформации (взаимные повороты).
Нагрузка приложена в узлах. Для узловой передачи нагрузки на практике
используются специальные балочные конструкции.
3. Геометрические размеры фермы не изменяются при нагружении (деформации малы).
■ Метод вырезания узлов – Последовательно вырезаются узлы фермы так, чтобы
в двух уравнениях равновесия для каждого из узлов было не более двух неизвестных
усилий. Как правило внешние опорные реакции должны быть предварительно определены.
2. Нумеруем или обозначаем буквами необозначенные узлы. Реакции стержней (или
усилия в них) будем обозначать далее двумя индексными цифрами или буквами – первая из
них совпадает с номером (обозначением) вырезаемого узла, а вторая указывает к каком узлу
присоединяется другим концом рассматриваемый стержень.
3. Вырезаем узел A (в этом узле всего два неизвестных усилия) и заменяем действие разрезанных
(отброшенных) узлов усилиями (реакциями) SA1 и SA6.
1
2
3
4
5
6
7
8
A
4. Составляем уравнения равновесия для узла A и вычисляем усилия SA1 и SA6.
5. Вырезаем узел 1 (в этом узле всего два неизвестных усилия) и заменяем действие разрезанных
(отброшенных) узлов усилиями (реакциями) S1A, S12 и S16.
1
6. Составляем уравнения равновесия для узла 1 и вычисляем усилия S12 и S16 (S1A и SA1 равны
алгебраически, поскольку при направлении неизвестных усилий от узла аксиома действия и проти-
водействия выполняется автоматически).
Порядок расчета:
1. Выбираем в качестве объекта равновесия ферму в целом и определяем опорные реакции:
Далее процесс вырезания узлов и
определения усилий повторяется
в определенном порядке, например:
2, 6, 7, 3, 4, 8, 5.
Вырезание последнего узла B может служить для контроля правильности расчета.
10

Лекция 4 (продолжение – 4.2)
Метод вырезания узлов для вычисления усилия только в указанном стержне требует рассмотрения всех узлов и решения для них уравнений
равновесия (по крайней мере узлов, находящихся между одним из опорных узлов и узлом, к которому подходит указанный стержень). Кроме того,
последовательное вычисление усилий и подстановка результатов в дальнейший расчет при большом числе узлов чревато накоплением ошибок,
не говоря уже о том, допущенная грубая ошибка в одном из узлов делает дальнейшие вычисления неверными.
■ Метод сквозных сечений (метод Риттера) в большинстве случаев не требует для вычисления усилия только в указанном стержне составления
каких-либо других вспомогательных уравнений равновесия кроме того уравнения, в котором непосредственно участвует искомое усилие.
Метод основывается на составлении одного уравнения равновесия с использованием II и III форм уравнений равновесия произвольной плоской
системы сил.
Порядок расчета:
1. Выбираем в качестве объекта равновесия ферму в целом и определяем опорные реакции:
A
B
h
l
d
1
2
3
4
5
6
7
8
2. Проводим сквозное сечение, разделяющее ферму на две отдельные части так,
чтобы в сечение попадало не более трех стержней, в одном из которых требуется
найти усилие, например, сечение I-I для определения S23.
I
I
3. Выбирая в качестве объекта равновесия одну часть, например, правую, отбрасываем
другую (левую) часть.
4. Действие отброшенной части на оставшуюся заменяем реакциями стержней, попавших
в разрез – S32, S36 и S76.
5. Для искомого усилия S32 находим положение точки Риттера, как точки пересечения
линий действия двух других усилий S36 и S76, не подлежащих определению в данный момент.
Точка Риттера для усилия S32 совпадает с узлом 6.
6. Составляем моментное уравнение равновесия для оставленной (правой) части относительно
найденной точки Риттера (узла 6) и определяем искомое усилие.
7. Для определения усилия S76 находим положение точки Риттера, как точки пересечения
линий действия двух других усилий S36 и S32, не подлежащих определению в данный момент.
Точка Риттера для усилия S76 совпадает с узлом 3.
8. Составляем моментное уравнение равновесия для оставленной (правой) части относительно
найденной точки Риттера (узла 3) и определяем искомое усилие.
7. При определении усилия S36 точка Риттера, как точка пересечения линий действия двух других
усилий S76 и S32, не подлежащих определению в данный момент, уходит в бесконечность.
В этом случае моментное уравнение равновесия вырождается в уравнение равновесия в проекциях
на ось, перпендикулярную линиям, уходящим в бесконечность.
Для определения других усилий необходимо провести другое сечение (п.2)
и повторить описанные действия (пп. 3,4,….)
11

Лекция 4 (продолжение – 4.3 – дополнительный материал)
■ Понятия о линиях влияния опорных реакций и усилий. Железнодорожные мосты, сооружаемые с использованием таких элементов, как
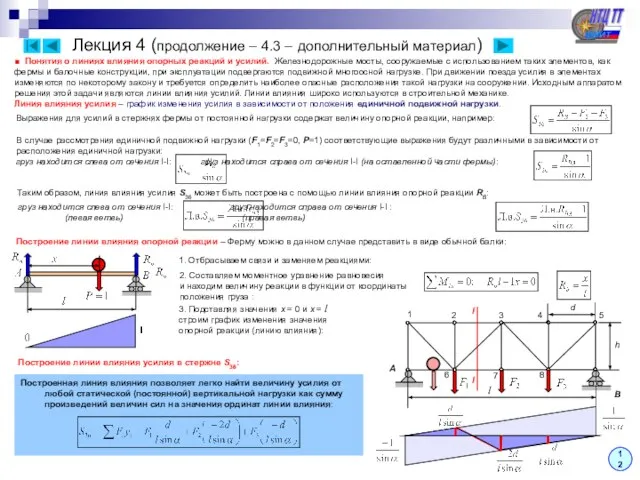
фермы и балочные конструкции, при эксплуатации подвергаются подвижной многоосной нагрузке. При движении поезда усилия в элементах
изменяются по некоторому закону и требуется определить наиболее опасные расположения такой нагрузки на сооружении. Исходным аппаратом
решения этой задачи являются линии влияния усилий. Линии влияния широко используются в строительной механике.
Линия влияния усилия – график изменения усилия в зависимости от положения единичной подвижной нагрузки.
Выражения для усилий в стержнях фермы от постоянной нагрузки содержат величину опорной реакции, например:
В случае рассмотрения единичной подвижной нагрузки (F1=F2=F3=0, P=1) соответствующие выражения будут различными в зависимости от
расположения единичной нагрузки:
груз находится слева от сечения I-I: груз находится справа от сечения I-I (на оставленной части фермы):
Таким образом, линия влияния усилия S36 может быть построена с помощью линии влияния опорной реакции RB:
груз находится слева от сечения I-I: груз находится справа от сечения I-I :
(левая ветвь) (правая ветвь)
Построение линии влияния опорной реакции – Ферму можно в данном случае представить в виде обычной балки:
1. Отбрасываем связи и заменяем реакциями:
2. Составляем моментное уравнение равновесия
и находим величину реакции в функции от координаты
положения груза :
3. Подставляя значения x = 0 и x = l
строим график изменения значения
опорной реакции (линию влияния):
Построение линии влияния усилия в стержне S36:
A
B
h
l
d
1
2
3
4
5
6
8
I
7
1. Строим левую ветвь л.в. усилия (груз находится слева) используя
соответствующее выражение :
2. Строим правую ветвь л.в. усилия (груз находится справа) используя
соответствующее выражение :
3. Строим передаточную прямую, учитывающую узловую передачу нагрузки :
Построенная линия влияния позволяет легко найти величину усилия от любой статической (постоянной) вертикальной нагрузки как сумму произведений величин сил на значения ординат линии влияния:
I
12

Лекция 4 (продолжение – 4.4)
■ Равновесие сочлененных тел. Железнодорожные и строительные конструкции могут состоять из сочлененных между собой тел (балок, ферм).
Количество наложенных связей может превышать число независимых уравнений равновесия, которые можно составить для рассматриваемой
конструкции. Такие задачи являются статически неопределимыми. Степень статической неопределимости для плоских систем равна:
где Д – число жестких дисков, Ж – число жестких заделок,
Ш – число неподвижных шарниров (опорных и соединяющих диски между собой,
С – число шарнирных стержней (опорных или соединяющих диски между собой) или подвижных шарниров
B
1. Выберем в качестве объекта всю конструкцию.
С
B
В теоретической механике возможно решение только статически определимых задач, в которых количество связей равно числу независимых уравнений равновесия (n = 0).
2. Отбросим связи и заменим их действие реакциями.
3. Число неизвестных реакций – 4, а количество независимых уравнений - 3.
Это означает, что необходимо расчленить конструкцию – отбросить шарнир C
и заменить его действие на каждую из частей реакциями.
4. Число неизвестных реакций – 8, а количество независимых
уравнений равновесия для обоих частей - 3·2 = 6.
С использованием аксиомы действия и противодействия для каждой пары
реакций шарнира C общее число неизвестных реакций уменьшается до 6
и равно общему числу уравнений равновесия:
5. Решение полученной системы уравнений не представляет особых
затруднений в указанном порядке: от вспомогательной балки CB (не может оставаться в равновесии без балки AC) к основной балке AC (может находиться в равновесии без балки CB).
■ Равновесие рычага. Рычаг – твердое тело, имеющее одну неподвижную точку.
Рычаг имеет одну степень кинематической подвижности (w = – n = 3Д – 3Ж – 2Ш – С =
= 3·1 – 3·0 – 2·1 – 0 = 1) и в равновесии может быть лишь при определенном
соотношении активных сил, действующих на рычаг.
A
■ Уравнения равновесия рычага. Применяя общий подход составления уравнений
равновесия к рычагу получаем:
Во многих случаях значением опорных реакций не интересуются и искомое соотношение сил определяют из последнего моментного уравнения, которое и принимается за уравнение равновесия рычага.
Уравнение равновесия рычага используется при расчете подпорной стенки или груза на опрокидывание:
A
Условие устойчивости на опрокидывание: Удерживающий момент относительно неподвижной точки (от F1)
должен быть больше опрокидывающего момента (от F2) относительно этой же точки.
13