Прогнозирование цен на товары или активы

2
Предположим, что даны примеры n наблюдений, как показано, мы установили модель ценообразования с k-1 характеристиками.
PREDICTION
True model
Fitted model

3
Предположим сейчас, что оно сталкивается с новым видом товара с характеристиками {X2*, X3*, ..., Xk* }. Учитывая (пример) результат выборки регрессии, естественно прогнозировать, что цена нового вида должна сводиться к третьему уравнению.
PREDICTION
Prediction conditional on
True model
Fitted model

4
Что же можно сказать о свойствах этого прогнозирования? Во-первых, естественно спросить справедливо ли оно в НЕсистематической переоценке или недооценке смысла фактической цены. Во-вторых, мы обеспокоены о вероятной точности прогноза
PREDICTION
Prediction conditional on
True model
Fitted model

5
PREDICTION
Мы будем рассматривать пример, где товар имеет одну соответствующую характеристику и предположим, что мы установили простую регрессионную показанную модель. Следовательно, дадим новый вид товара с характеристиками X = X * , эта модель дает нам прогнозируемую цену.
Prediction conditional on
True model
Fitted model

6
PREDICTION
Допустим, что модель относится (обращается) к новому товару и, следовательно, к фактической цене, условно X = X *; оно образуется как показано, где u* - это значение нарушения условия нового товара.
Prediction conditional on
True model
Fitted model
Actual value of

7
PREDICTION
Мы объясним ошибку прогнозирования модели PE, как разницу между ценой фактической и прогнозируемой
Prediction conditional on
True model
Fitted model
Actual value of

8
Прогнозируемая ошибка получается путем подстановки фактической и прогнозируемой цены.
PREDICTION
Prediction conditional on
True model
Fitted model
Actual value of

9
PREDICTION
Мы ожидаем.
Prediction conditional on
True model
Fitted model
Actual value of

10
PREDICTION
β1 и β2 приняты с фиксированными параметрами, поэтому ожидания на них не влияют. Также X * принято считать фиксированной величиной и также ожидания не воздействуют. Тем не менее, u* и случайные переменные.
Prediction conditional on
True model
Fitted model
Actual value of

11
PREDICTION
E(u*) = 0 потому что u* выявлено случайно из распределения для u, который мы приняли как нулевую совокупность. В соответствии с обычными предположениями МНК есть несмещенная оценка β1 и является несмещенной оценкой
Prediction conditional on
True model
Fitted model
Actual value of

12
PREDICTION
Следовательно, ожидание ошибки прогнозирования равен нулю. Результат легко обобщается в случае, где множественные характеристики и новые товары включают в себя новую комбинацию
Prediction conditional on
True model
Fitted model
Actual value of

13
Показана дисперсия совокупности ошибки прогнозирования. Неудивительно, что это подразумевает, далее - значение X * от среднего значения выборки, что дисперсия совокупности ошибки прогнозирования будет больше.
PREDICTION
Variance of prediction error

14
Также подразумевается, что снова неудивительно, что тем больше образец, тем меньше будет дисперсия совокупности ошибки прогнозирования с нижним лимитом σu2
PREDICTION
Variance of prediction error

15
При условии, что допущения модели регрессии действительны, и будут стремиться к их реальным значениям, так как образец становится больше, поэтому единственным источником ошибки в прогнозировании будет u*, и по определению оно имеет дисперсию совокупности σu2.
PREDICTION
Variance of prediction error

16
Стандартная ошибка прогнозирования вычисляется используя квадратный корень выражения для дисперсии совокупности, заменяя дисперсию u с оценкой, полученной при подгонке модели в период выборки.
PREDICTION
Standard error
Variance of prediction error

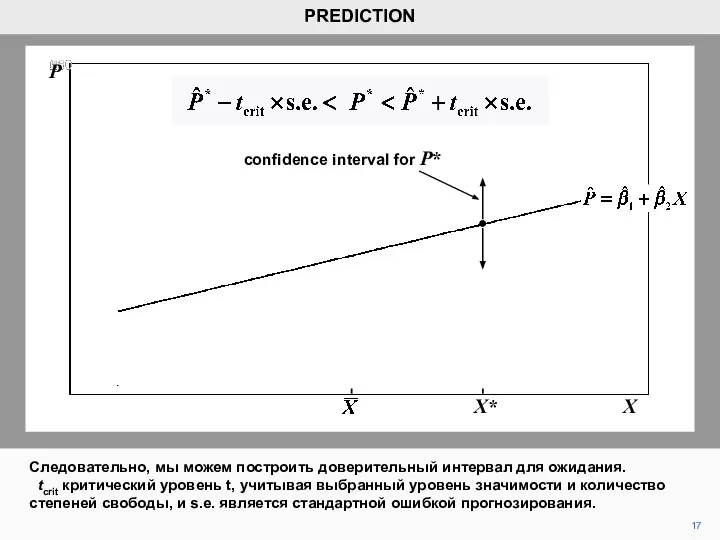
17
Следовательно, мы можем построить доверительный интервал для ожидания.
tcrit критический уровень t, учитывая выбранный уровень значимости и количество степеней свободы, и s.e. является стандартной ошибкой прогнозирования.
PREDICTION
P
X
X*
upper limit of confidence interval for P*

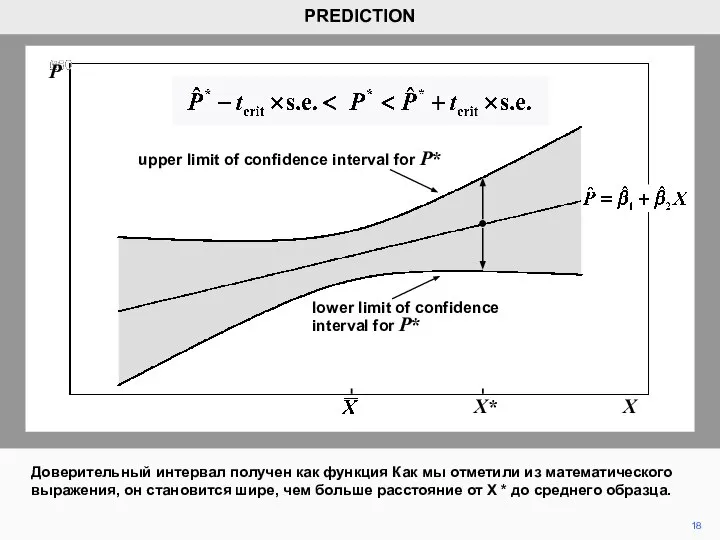
18
Доверительный интервал получен как функция Как мы отметили из математического выражения, он становится шире, чем больше расстояние от X * до среднего образца.
PREDICTION
P
X
X*
upper limit of confidence interval for P*
lower limit of confidence
interval for P*

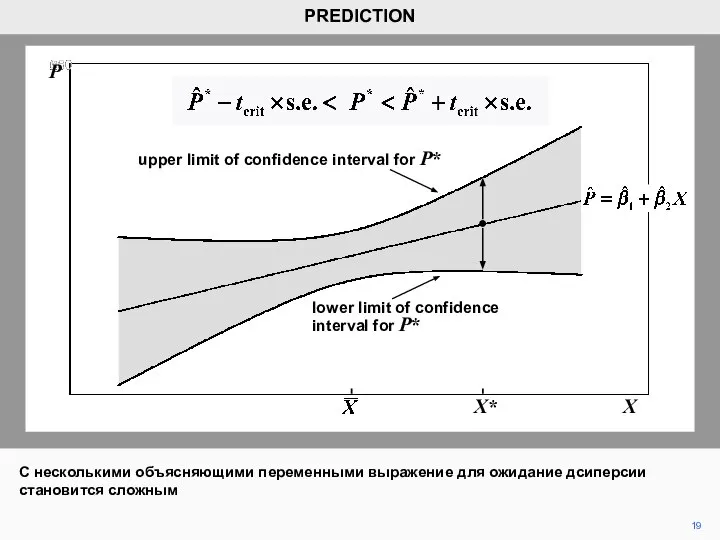
19
PREDICTION
P
X
X*
upper limit of confidence interval for P*
lower limit of confidence
interval for P*
С несколькими объясняющими переменными выражение для ожидание дсиперсии становится сложным

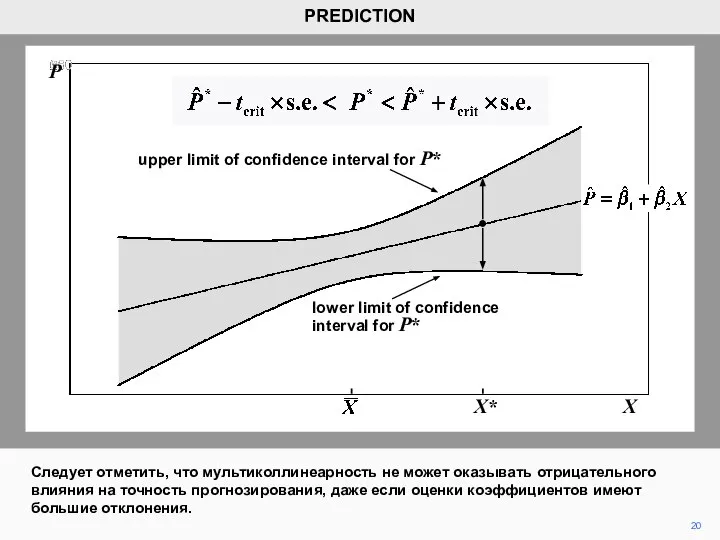
20
PREDICTION
P
X
X*
upper limit of confidence interval for P*
lower limit of confidence
interval for P*
Следует отметить, что мультиколлинеарность не может оказывать отрицательного влияния на точность прогнозирования, даже если оценки коэффициентов имеют большие отклонения.

21
PREDICTION
Для простоты предположим, что есть две объясняющие переменные, что оба имеют положительные истинные коэффициенты и как показано, они положительно коррелированы; мы прогнозируем значение Y *, учитывая значения X2 * и X3 *.
Suppose X2 and X3 are positively correlated, β2 > 0, β3 > 0.
Then .
If is overestimated, is likely to be underestimated.
So may be a good estimator of .
Similarly, for other combinations.

22
Тогда, если эффект от X2 переоценен, поэтому > β2, эффект от X3 вероятно будет недооценена с < β3. Как следствие, эффекты ошибки могут в какой-то мере отмениться, в результате линейная комбинация может быть приближена к (β2X2* + β3X3*)
PREDICTION
Suppose X2 and X3 are positively correlated, β2 > 0, β3 > 0.
Then .
If is overestimated, is likely to be underestimated.
So may be a good estimator of .
Similarly, for other combinations.

23
Это будет проиллюстрировано с моделированием, с моделью и показанными данными. Мы устанавливаем модель и делаем прогноз
Simulation
PREDICTION

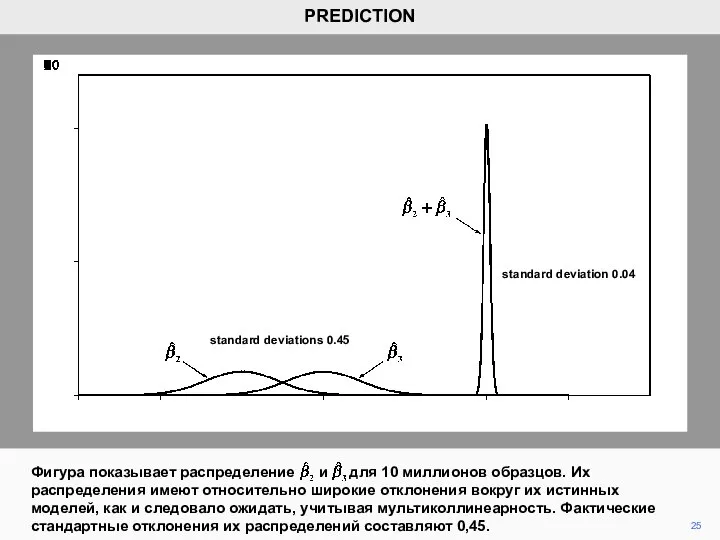
24
Поскольку X2 и X3 практически идентичны, они могут приблизиться к
Таким образом, точность прогноза зависит как близко к (β2 + β3), то есть 5
PREDICTION
Simulation

25
Фигура показывает распределение и для 10 миллионов образцов. Их раcпределения имеют относительно широкие отклонения вокруг их истинных моделей, как и следовало ожидать, учитывая мультиколлинеарность. Фактические стандартные отклонения их распределений составляют 0,45.
PREDICTION
standard deviations 0.45
standard deviation 0.04