Содержание
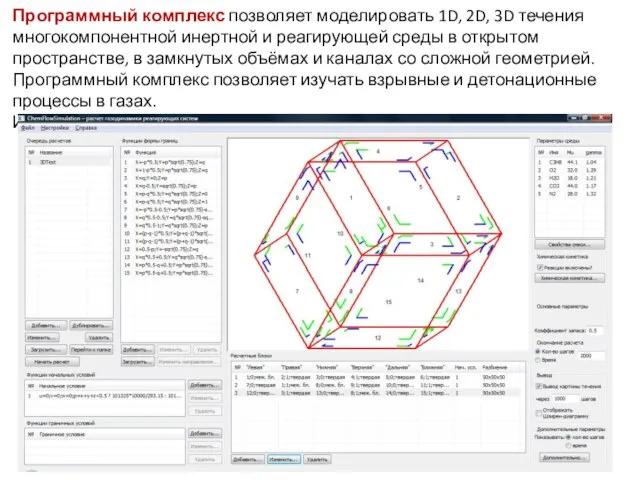
- 2. Программный комплекс позволяет моделировать 1D, 2D, 3D течения многокомпонентной инертной и реагирующей среды в открытом пространстве,
- 3. Заложенная математическая модель. Уравнения движений многокомпонентной реагирующей среды Уравнения Эйлера – уравнения плоских движений – уравнения
- 4. Заложенная математическая модель. Уравнения течений многокомпонентной реагирующей среды Используются уравнения Эйлера для плоских, осесимметричных и трехмерных
- 5. Химическая кинетика горения Пропановоздушная смесь, N=5 компонентов: C3H8, O2, H2O, CO2, N2 Скорость реакции: Используется одностадийная
- 6. Программный комплекс основан на модифицированном методе С.К. Годунова, хорошо зарекомендовавшем себя при расчете течений газовых смесей
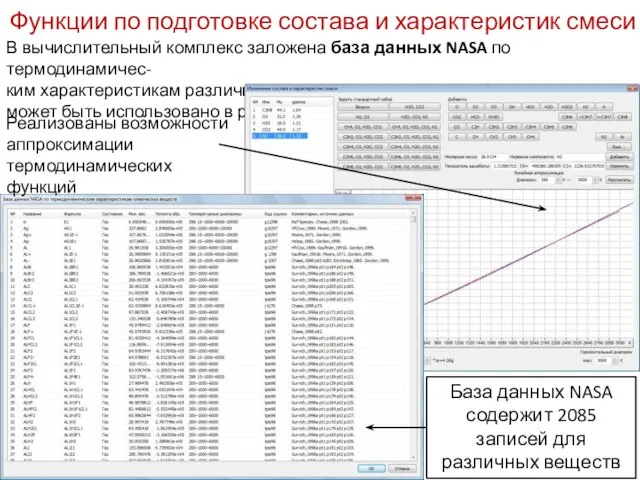
- 7. В вычислительный комплекс заложена база данных NASA по термодинамичес- ким характеристикам различных химических веществ, любое вещество
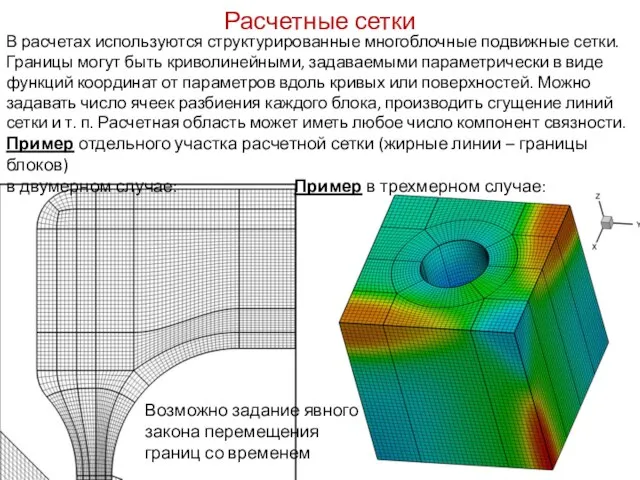
- 8. В расчетах используются структурированные многоблочные подвижные сетки. Границы могут быть криволинейными, задаваемыми параметрически в виде функций
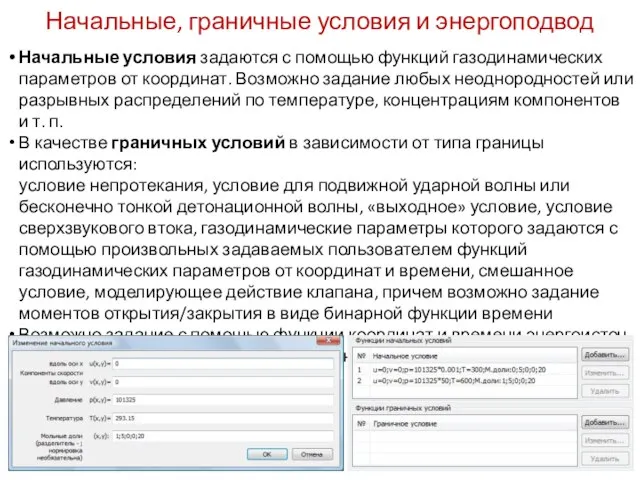
- 9. Начальные, граничные условия и энергоподвод Начальные условия задаются с помощью функций газодинамических параметров от координат. Возможно
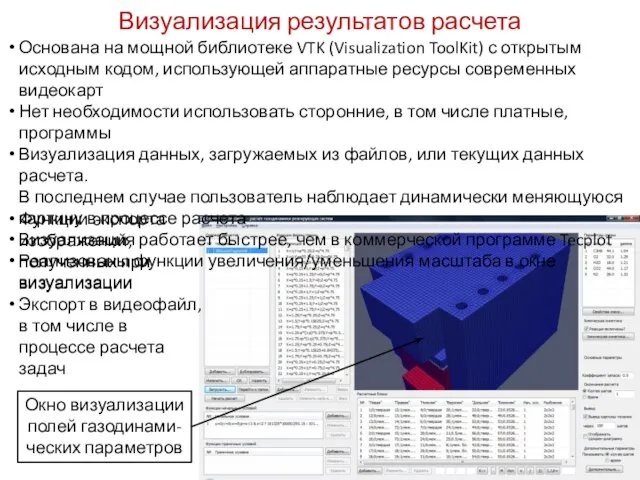
- 10. Основана на мощной библиотеке VTK (Visualization ToolKit) с открытым исходным кодом, использующей аппаратные ресурсы современных видеокарт
- 11. Примеры расчетов ячеистой детонации
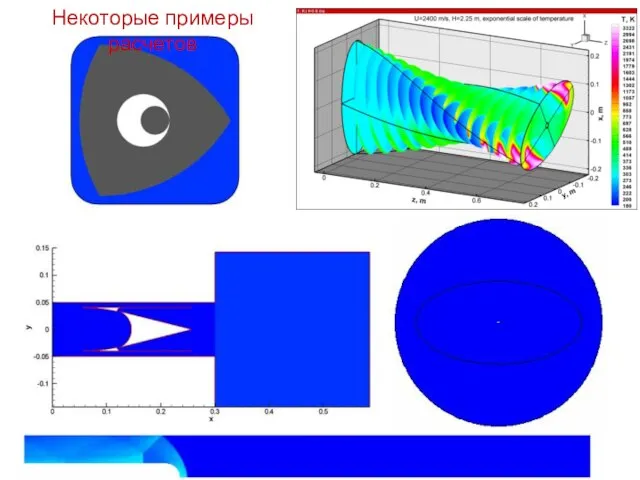
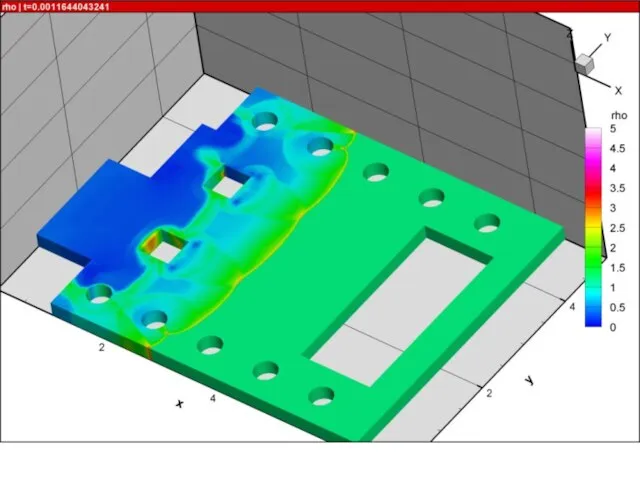
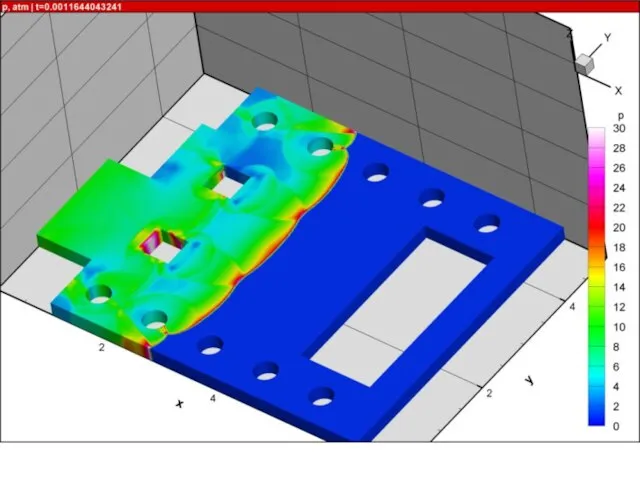
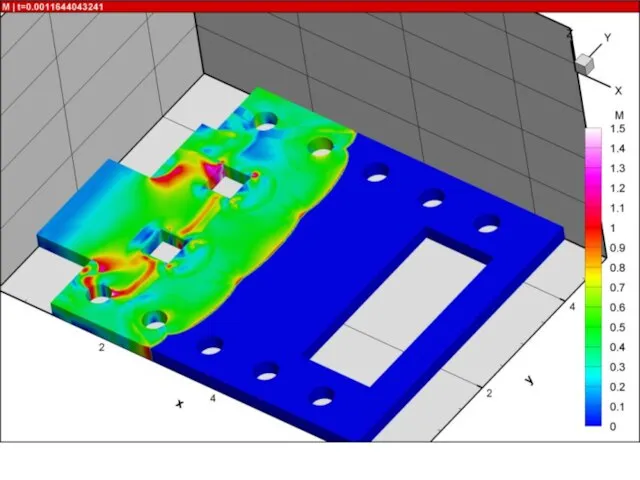
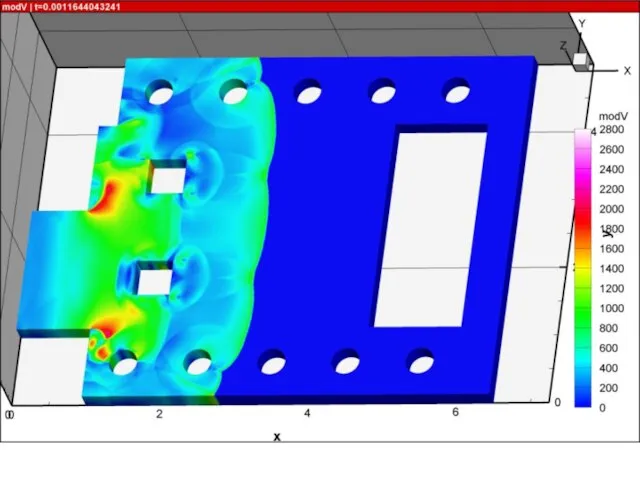
- 12. Некоторые примеры расчетов
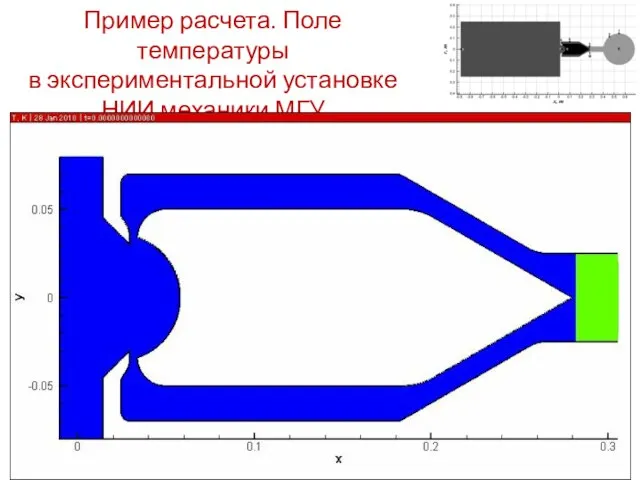
- 13. Пример расчета. Поле температуры в экспериментальной установке НИИ механики МГУ
- 14. Детонация во вращающемся цилиндре с уступами параболической формы Поле давления Величина критической угловой скорости, начиная с
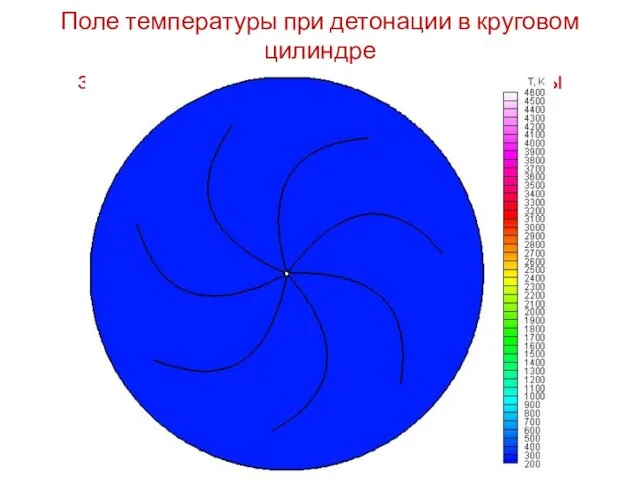
- 15. Поле температуры при детонации в круговом цилиндре за счет вращения звездообразной фигуры
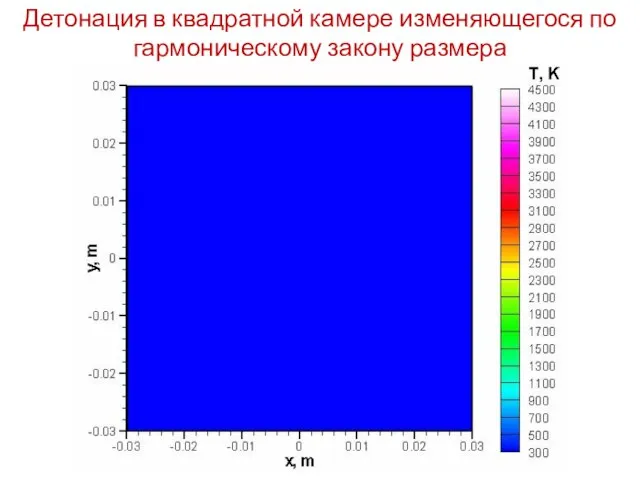
- 16. Детонация в квадратной камере изменяющегося по гармоническому закону размера
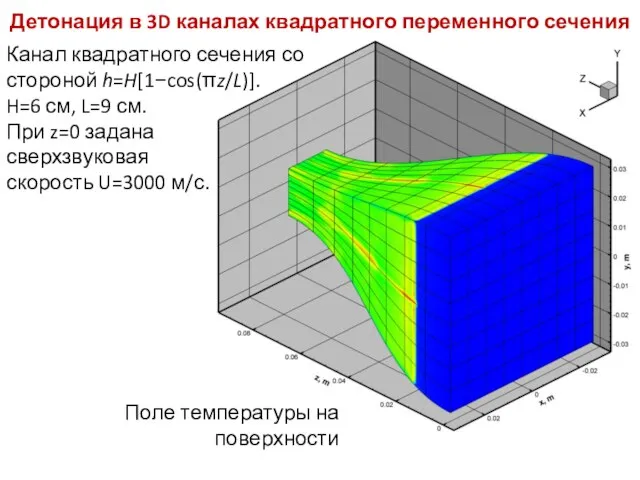
- 17. Детонация в 3D каналах квадратного переменного сечения Канал квадратного сечения со стороной h=H[1−cos(πz/L)]. H=6 см, L=9
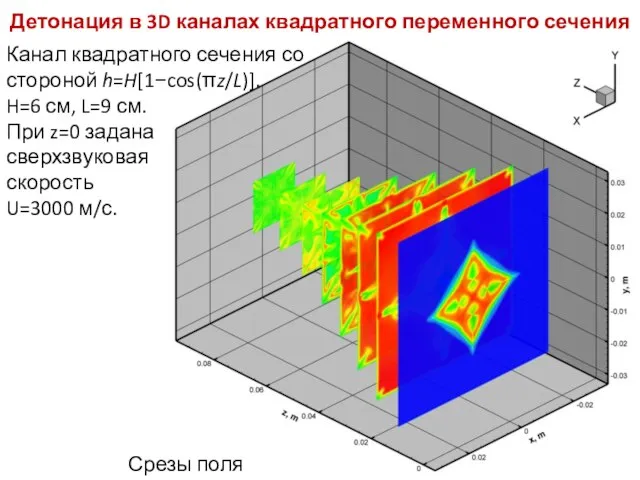
- 18. Детонация в 3D каналах квадратного переменного сечения Канал квадратного сечения со стороной h=H[1−cos(πz/L)]. H=6 см, L=9
- 19. Срезы поля температуры
- 20. Проведение расчетов на многоядерных процессорах, кластерах и суперкомпьютерах В программе под Windows произведено распараллеливание расчета задач
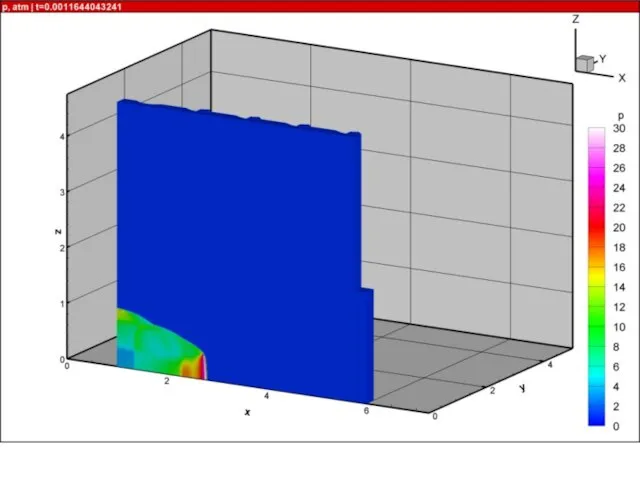
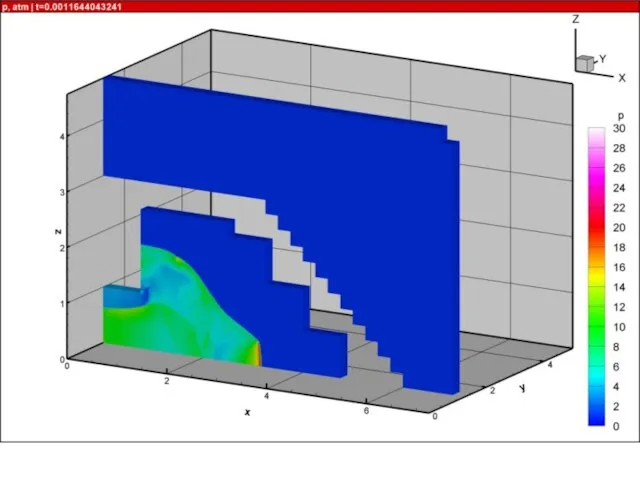
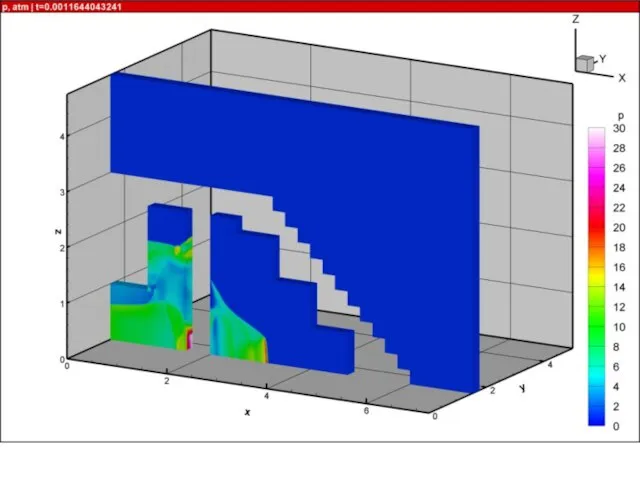
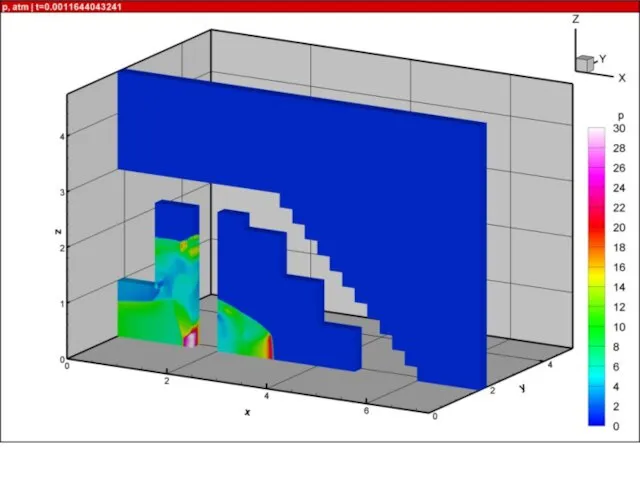
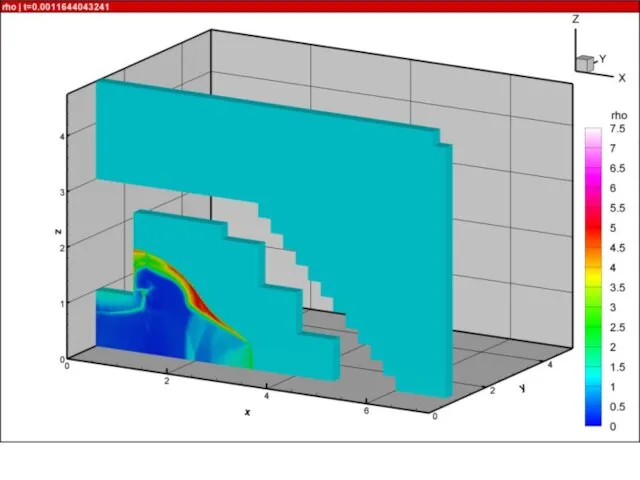
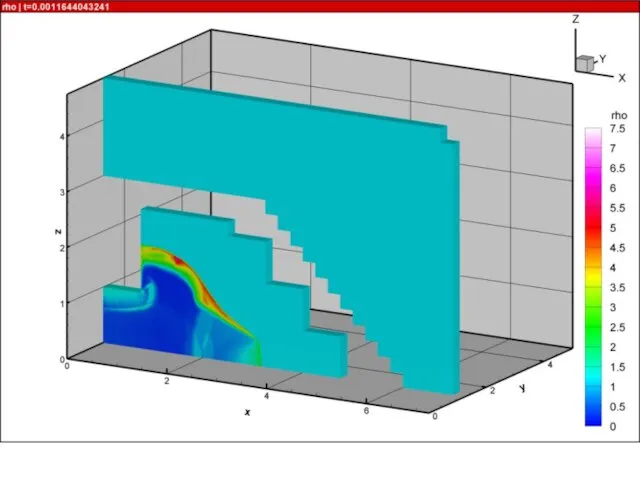
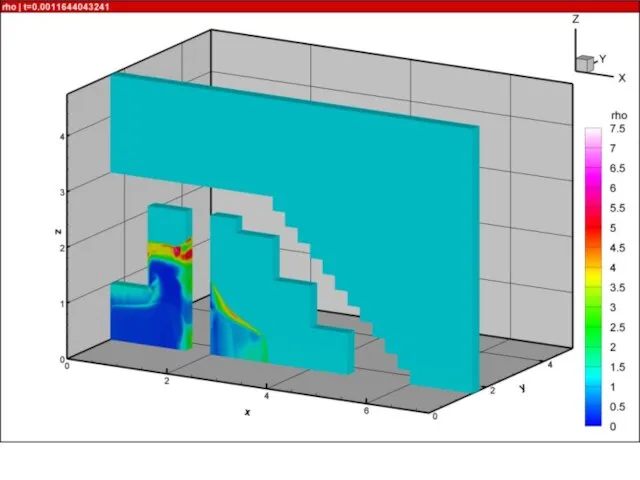
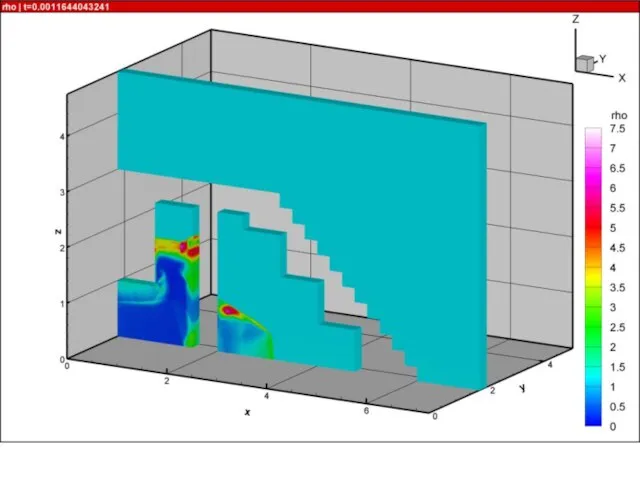
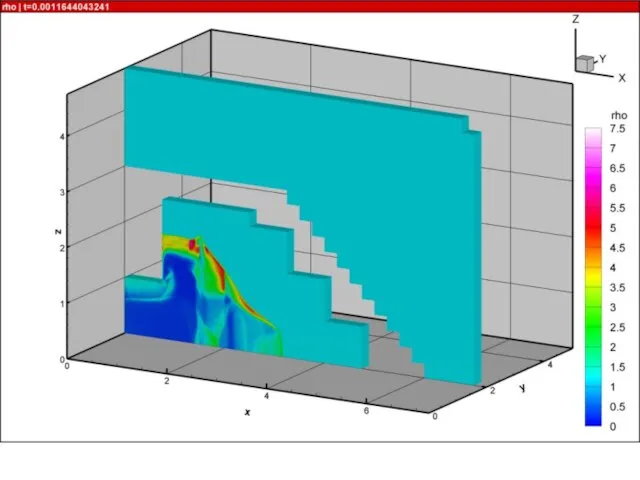
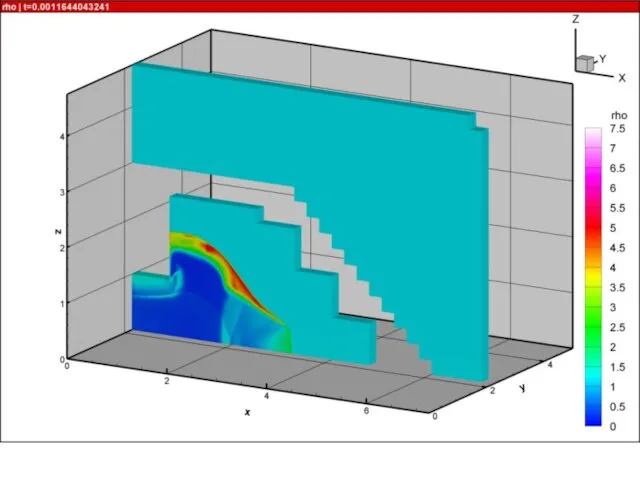
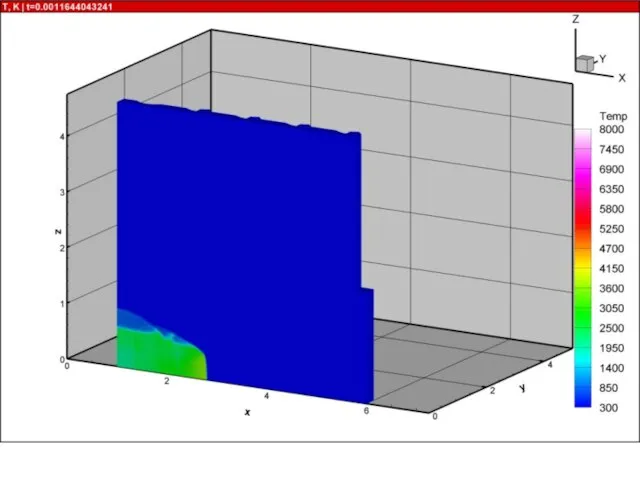
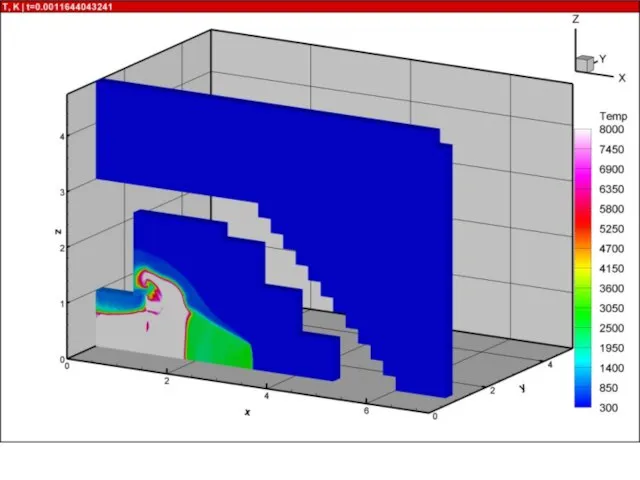
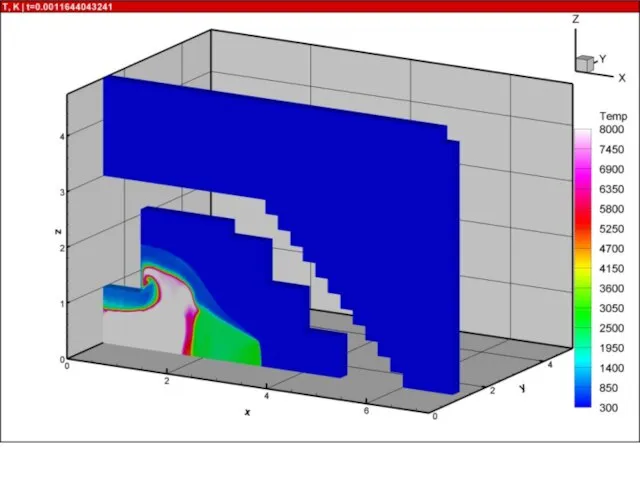
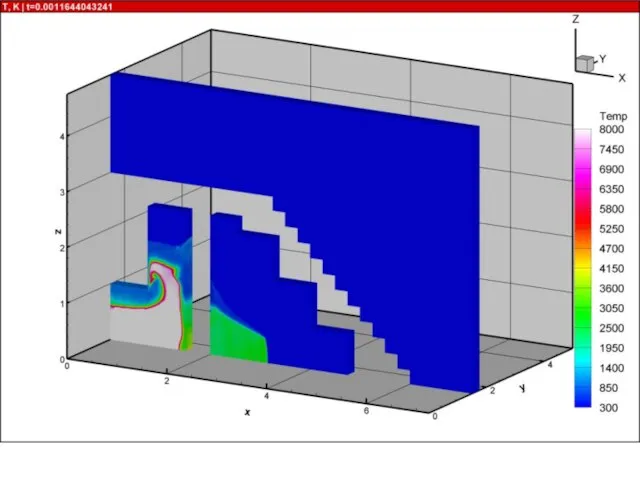
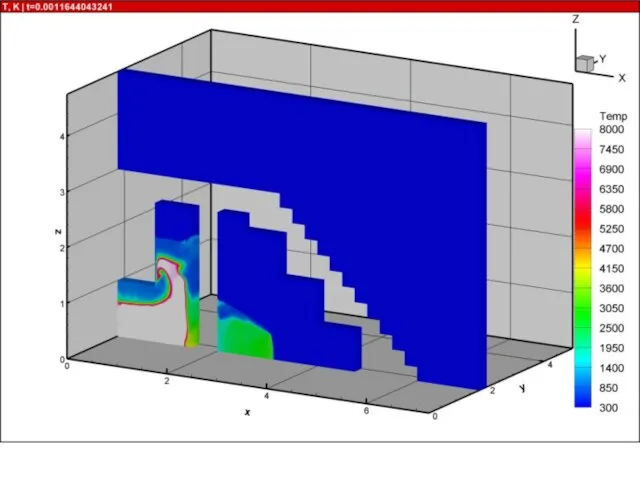
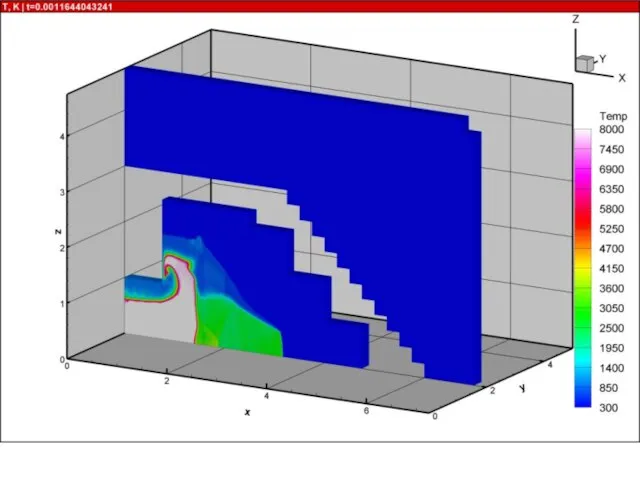
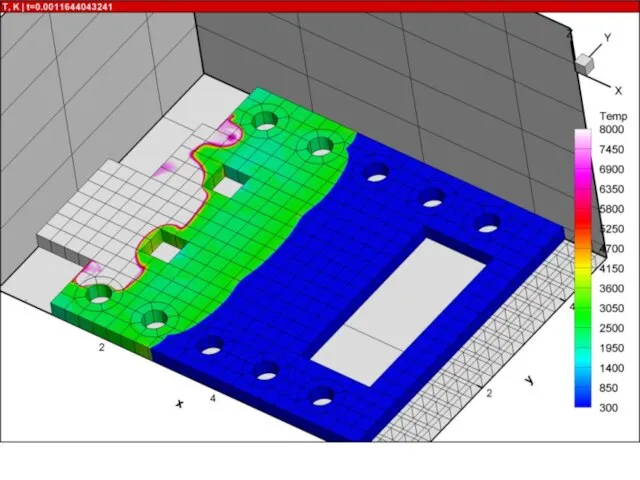
- 21. Результаты расчетов на суперкомпьютере «Ломоносов» взрыва в комнате с колоннами и лестницей 10000 расчетных блоков, практически
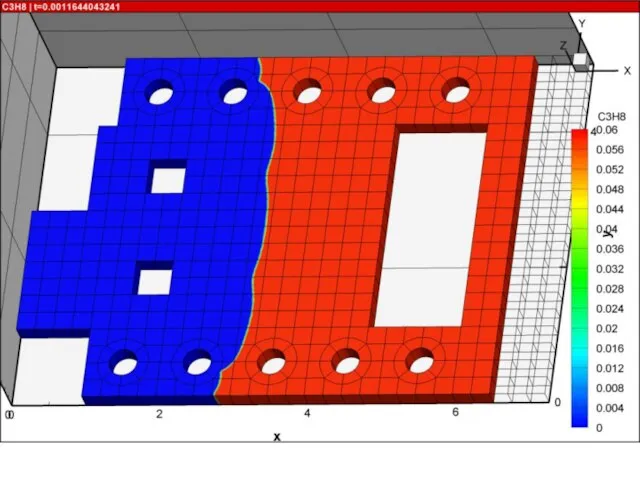
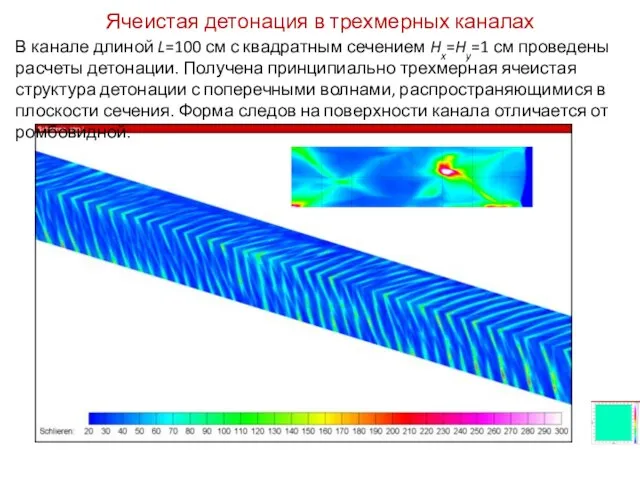
- 52. Ячеистая детонация в трехмерных каналах В канале длиной L=100 см с квадратным сечением Hx=Hy=1 см проведены
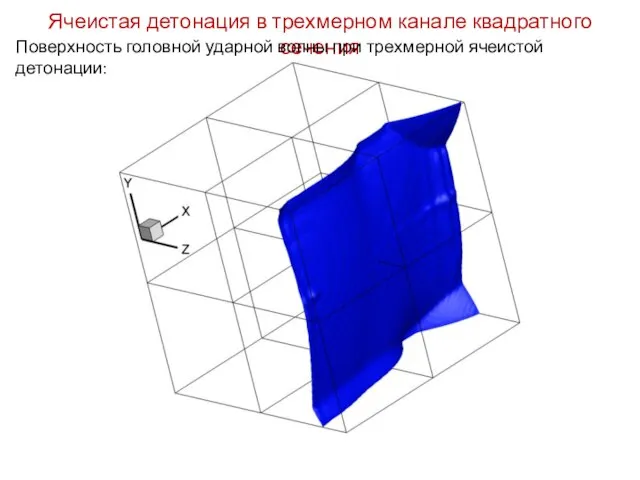
- 53. Ячеистая детонация в трехмерном канале квадратного сечения Поверхность головной ударной волны при трехмерной ячеистой детонации:
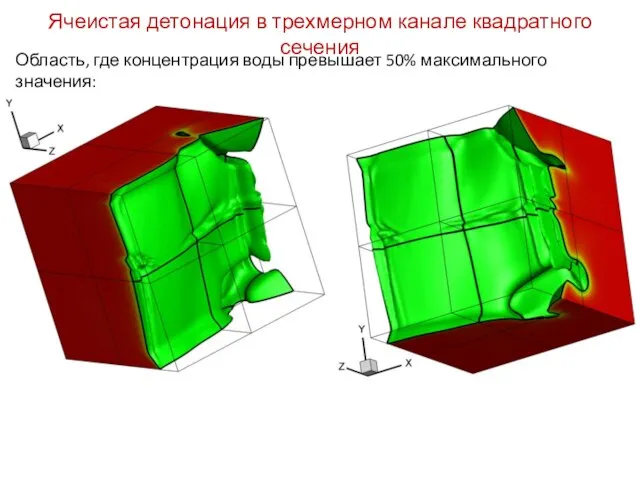
- 54. Ячеистая детонация в трехмерном канале квадратного сечения Область, где концентрация воды превышает 50% максимального значения:
- 55. Ячеистая детонация в трехмерном канале круглого сечения В каналах круглого сечения также возникает сложная структура поперечных
- 56. Реализован вычислительный комплекс для моделирования пространственных течений многокомпонентной инертной и реагирующей среды в открытом пространстве, в
- 58. Скачать презентацию



















 Молодежные организации в России
Молодежные организации в России ООО МПК «СОАР»
ООО МПК «СОАР» Презентация1
Презентация1 Зимние виды спорта
Зимние виды спорта Муниципальное дошкольное образовательное учреждение «Центр развития ребенка – детский сад имени Д.Г. Готовцевой»Амгинский улус
Муниципальное дошкольное образовательное учреждение «Центр развития ребенка – детский сад имени Д.Г. Готовцевой»Амгинский улус Задачи на движение по воде
Задачи на движение по воде Знакомство практикантов с топ-персоналом компании 100 Клиентов
Знакомство практикантов с топ-персоналом компании 100 Клиентов Достопримечательности Вены
Достопримечательности Вены Інжу слайд 2
Інжу слайд 2 ДИФФЕРЕНЦИАЛЬНАЯ ДИАГНОСТИКА ПУЛЬПИТОВ. ВЫБОР МЕТОДА ЛЕЧЕНИЯ ПУЛЬПИТОВ НА ОСНОВАНИИ ПАТОГЕНЕТИЧЕСКИХ ОСОБЕННОСТЕЙ РАЗВИТИЯ РАЗ
ДИФФЕРЕНЦИАЛЬНАЯ ДИАГНОСТИКА ПУЛЬПИТОВ. ВЫБОР МЕТОДА ЛЕЧЕНИЯ ПУЛЬПИТОВ НА ОСНОВАНИИ ПАТОГЕНЕТИЧЕСКИХ ОСОБЕННОСТЕЙ РАЗВИТИЯ РАЗ Тренировка ума и характера
Тренировка ума и характера ЛОЯЛЬНОСТЬ К ПОТРЕБИТЕЛЮ
ЛОЯЛЬНОСТЬ К ПОТРЕБИТЕЛЮ Выставка кроссвордов учащихся школ района «Будь здоров!» в рамках фестиваля «Мы – за здоровый город!» 15 ноября – 15 декабря 2010 г.
Выставка кроссвордов учащихся школ района «Будь здоров!» в рамках фестиваля «Мы – за здоровый город!» 15 ноября – 15 декабря 2010 г. Презентация2
Презентация2 Семинар №2Метод кейс-стади в образовании
Семинар №2Метод кейс-стади в образовании Доблесть и честь
Доблесть и честь Дефисное написание наречий
Дефисное написание наречий Рисунок скелета грудной клетки и таза
Рисунок скелета грудной клетки и таза Территориально – производственная структура нефтяной промышленности РФ
Территориально – производственная структура нефтяной промышленности РФ Какими природными ресурсами богата наша страна?
Какими природными ресурсами богата наша страна? Политическое сознание
Политическое сознание 20140513_atmosfernoe_davlenie_film
20140513_atmosfernoe_davlenie_film Настоящая работа выполнена в кружке “Юный изобретатель” при МОУ “Центр образования №8”
Настоящая работа выполнена в кружке “Юный изобретатель” при МОУ “Центр образования №8” Хронология моды. 20 годы 20 века – 10 годы 21 века
Хронология моды. 20 годы 20 века – 10 годы 21 века Работа над радостностью
Работа над радостностью Валерий Яковлевич Брюсов
Валерий Яковлевич Брюсов Подход к ребенку
Подход к ребенку МОУ «Чечеульская СОШ»
МОУ «Чечеульская СОШ»