Производная в технике, физике, химии, экономике. . .»

Скажи мне, и я забуду. Покажи мне, и я запомню. Дай мне действовать самому,
И я научусь Конфуций
«…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…»
Н.И. Лобачевский
Производная в технике, физике, химии, экономике. . .»

ЦЕЛИ УРОКА:
∙ добиться усвоения учащимися систематических, осознанных сведений о понятии производной, её геометрическом и физическом смысле;
∙ формировать навыки практического использования производной в предметах школьного курса, показать применение производной при решении жизненно важных задач;
∙ развивать познавательный интерес у учащихся
через раскрытие практической необходимости и
теоретический значимости темы и использование возможностей ЭВМ в изучении темы;
∙ формировать у учащихся понятие о научной организации труда с помощью ЭВМ;

Кроссворд
" Мысли в фокус"

Блиц-опрос
1. Какая программа используется для организации работы кроссворда?
Электронная таблица (Excel)– это работающее в диалоговом режиме приложение, хранящее и обрабатывающее данные в прямоугольных таблицах
2. Сформулировать правила записи формул в Excel
Формула начинается со знака равенства и включает в себя имена ячеек, числа, функции и знаки математических операций. В формулу не может входить текст.
3. Определить тип ссылок, используемых при создании кроссворда.
Относительные ссылки

Какой результат будет вычислен в ячейке С2 после копирования в неё формулы из ячейки С1 ?
1) 75 2) 150 3) 50 4) 0

Блиц-опрос
Что называется производной функции в точке?
Ответ: производной функции у = f(x) в точке х0 называется предел отношения приращения функции в точке х0 к приращению аргумента, когда последнее стремится к нулю.
В чем заключается геометрический смысл производной?
Ответ: значение производной f '(x) при данном значении аргумента x равно тангенсу угла, образованного с положительным направлением оси Ox касательной к графику функции f(x) в точке M(x, f(x)).
k = tgα = f '(x0).
В чем заключается механический смысл производной?
Ответ: производная функции y = f(x) в точке x0 - это скорость изменения функции f (х) в точке x0
x'(t). = ν(t)

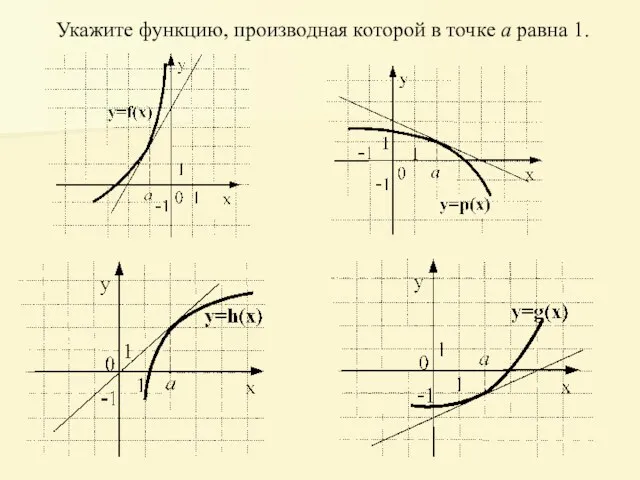
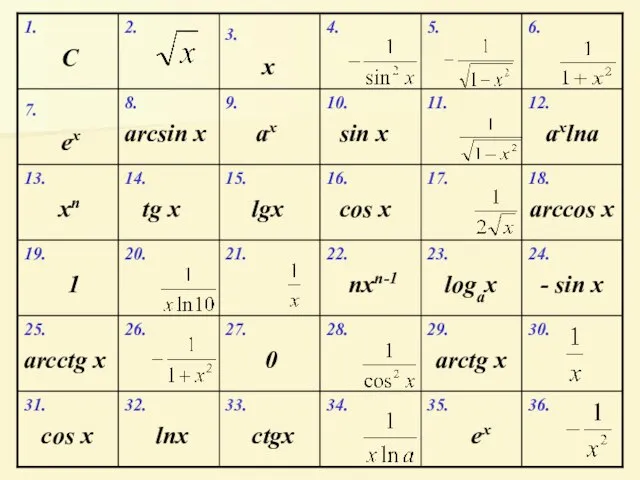
Укажите функцию, производная которой в точке а равна 1.

36.
35.
ex
34.
33.
ctgx
32.
lnx
31.
cos x
30.
29.
arctg x
28.
27.
0
26.
25.
arcctg x
24.
- sin x
23.
logax
22.
nxn-1
21.
20.
19.
1
18.
arccos x
17.
16.
cos x
15.
lgx
14.
tg x
13.
xn
12.
axlna
11.
10.
sin x
9.
аx
8.
arcsin x
7.
еx
6.
5.
4.
3.
x
2.
1.
С

Домашнее задание
Работа с информацией на электронных носителях
Найти в Интернете сайты по теме «Производная в физике, технике, химии, экономике…» и составить на каждый рецензию».
Работа с информацией на печатных носителях
Подготовить формулы из физики и экономики, химии…, где используется производная.

Программа решения задачи на языке Паскаль
Program shar;
Const P=3.14;
Var R, S : real;
Begin
Writeln ( ‘ ввести R ’ );
Readln ( R );
S = 4 * P * R * R;
Writeln( ‘ Площадь S= ’ , S );
Readln;
End.

υ(t) = х ′ (t) – скорость
a (t)=υ′ (t) - ускорение
J (t) = q′ (t) - сила тока
C(t) = Q′ (t) - теплоемкость
d(l)=m′ (l) - линейная плотность
K (t) = l/′ (t) - коэффициент линейного расширения
ω (t)= φ′ (t) - угловая скорость
а (t)= ω′ (t) - угловое ускорение
N(t) = A′ (t) - мощность
П (t) = υ′ (t) - производительность труда,
где υ (t) - объем продукции
J(x) = y′ (x) - предельные издержки производства, где y– издержки производства в зависимости от объема выпускаемой продукции x.

Исторические сведения
Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце 17 столетия на основе двух задач:
1) о разыскании касательной к произвольной линии
2) о разыскании скорости при произвольном законе движения
Еще раньше понятие производной встречалось в работах итальянского математика Тартальи (около 1500 - 1557 гг.) - здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.
В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л. Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.

Г. Лейбниц
И. Ньютон
Р. Декарт
Г.Галилей
Ж. Лагранж
Л. Эйлер

1. Пусть Q (t) количество теплоты, которое необходимо для нагревания тела массой 1 кг от 00С до температуры t0 (по Цельсию), известно, что в диапазоне 00 <= t <= 950, формула
Q (t) = 0,396 t + 2,081⋅10-3 t2 - 5,024⋅10-7 t3
дает хорошее приближение к истинному значению. Найдите, как зависит теплоёмкость воды от t.
C (t) = Q′(t) = 0,396 + 4,162⋅10 -3 t – 15,072⋅10 -7 t2

Пароход “Челюскин” в феврале 1934 года успешно прошел весь северный морской путь, но в Беринговом проливе оказался зажатым во льдах. Льды унесли “Челюскин” на север и раздавили.
Почему произошла катастрофа?
Сила Р давления льда разлагается на две: F и R. R – перпендикулярна к борту, F – направлена по касательной. Угол между P и R – a – угол наклона борта к вертикали.
Q – сила трения льда о борт.
Q = 0,2 R (0,2 – коэффициент трения).
Если Q < F, то F увлекает напирающий лед под воду, лед не причиняет вреда, если Q > F, то трение мешает скольжению льдины, и лед может смять и продавить борт.
0,2R < R tg α , tg α > 0,2
Q < F, если α > 110.
Наклон бортов корабля к вертикали под углом α > 110 обеспечивает безопасное плавание во льдах.

Выбрать оптимальный объем производства фирмой, функция прибыли которой может быть смоделирована зависимостью: π(q) = R(q) - C(q) = q2 - 8q + 10
Решение:
π'(q) = R'(q) - C'(q) = 2q - 8 = 0 → qextr = 4
При q < qextr = 4 → π'(q) < 0 и прибыль убывает
При q > qextr = 4 → π'(q) > 0 и прибыль возрастает
При q = 4 прибыль принимает минимальное значение.
Каким же будет оптимальный объем выпуска для фирмы? Если фирма не может производить за рассматриваемый период больше 8 единиц продукции (p(q = 8) = p(q = 0) = 10), то оптимальным решением будет вообще ничего не производить, а получать доход от сдачи в аренду помещений или оборудования. Если же фирма способна производить больше 8 единиц, то оптимальным для фирмы будет выпуск на пределе своих производственных мощностей.

м

Индивидуальная работа на ПК по
программе «1С Репетитор»
7 учащихся