Содержание
- 2. Цели урока: Образовательная; Развивающая; Воспитательная.
- 3. Образовательная: Отработка навыков и умений решения простейших задач в координатах и решения задач на скалярное произведение
- 4. Развивающая: Формирование умений выполнять обобщение; развитие качеств мышления: целенаправленность, рациональность; развитие самостоятельной деятельности учащихся на уроке.
- 5. Воспитательная: Воспитание интереса и любви к предмету; умения работать в коллективе; культуры общения.
- 6. План урока: Организационный момент. Сообщение темы и цели урока. Повторение: математический диктант с повторением теории. Решение
- 7. Повторение: Найти координаты вектора АВ, если А (3; -1; 2) и В (2; -1; 4).
- 8. Вопрос: Как найти координаты вектора, если известны координаты его начала и конца?
- 9. Ответ: A ( x ; y ; z ) B ( x ; y ; z
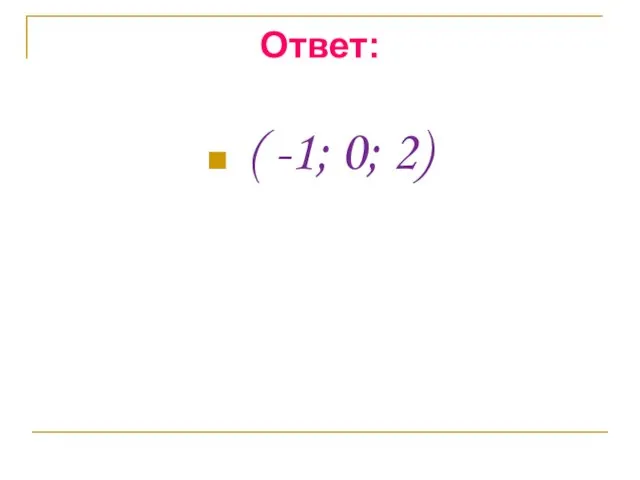
- 10. Ответ: ( -1; 0; 2)
- 11. Повторение: М – середина отрезка АВ. Найти координаты М, если А (0; 3; 4) и В
- 12. Вопрос: Как найти координаты середины отрезка?
- 13. Ответ: A ( x ; y ; z ) B ( x ; y ; z
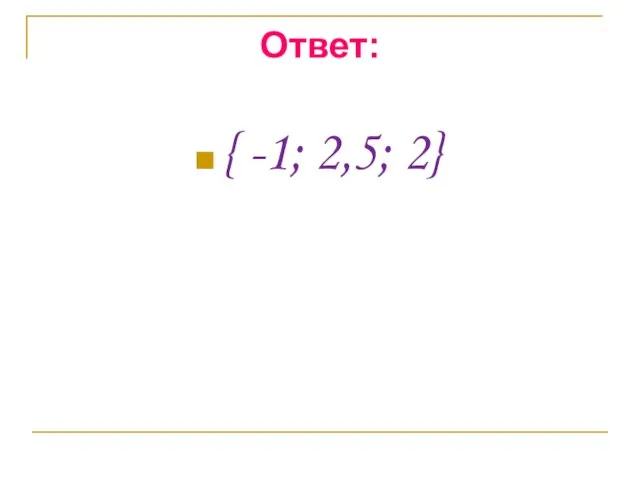
- 14. Ответ: { -1; 2,5; 2}
- 15. Повторение: Найти длину вектора а, если он имеет координаты: {-5; -1; 7}.
- 16. Вопрос: Как вычислить длину вектора по его координатам?
- 17. Ответ: Координаты вектора a { x ; y ; z } Длина вектора / a /
- 18. Ответ: 5 корней квадратных из 3
- 19. Повторение: Найти расстояние между точками А и В, если А (9; 3; -5) и В (2;
- 20. Вопрос: Как вычислить расстояние между точками?
- 21. Ответ: A ( x ; y ; z ) B ( x ; y ; z
- 22. Ответ: 7 корней квадратных из 2
- 23. Повторение: Найти скалярное произведение векторов: а {1; -1; 2} и в {5; 6; 2}.
- 24. Вопрос: Что называется скалярным произведением векторов?
- 25. Ответ: Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
- 26. Вопрос: Как вычислить скалярное произведение векторов по их координатам?
- 27. Ответ: Вектор a { x ; y ; z }, вектор в { x ; y
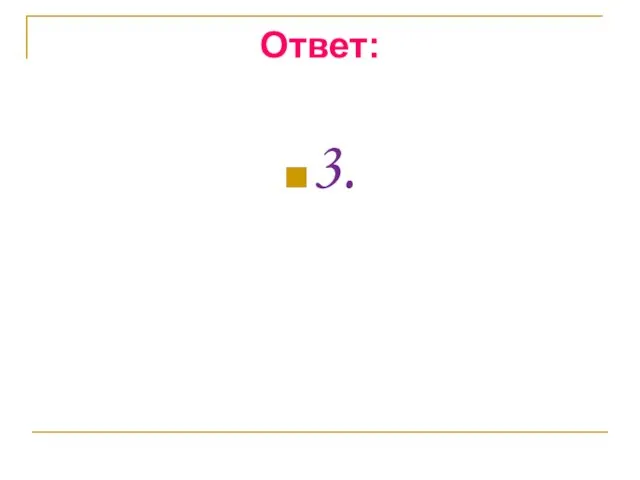
- 28. Ответ: 3.
- 29. Решение задач: Доказать, что четырехугольник ABCD является ромбом, если A (6; 7; 8), B (8; 2;
- 30. Решение:
- 31. Решение задач: № 453.
- 32. Решение:
- 33. Решение задач: Даны точки: А(1;2;3); В(2;3;1) и С(3;1;2). Найти периметр треугольника АВС.
- 34. Решение:
- 35. Решение задач: (по карточкам) Найти расстояние между точками В(-2;0;3) и К(3;4;-2). А(1;2;3) и В(3;-6;7). Найти координаты
- 36. Тест: I. Если М (-2; -4; 5), Р (-3; -5; 2), то МР имеет координаты: 1.
- 37. Тест: II. Если А (5; 4; 0), В (3; -6; 2) и С – середина отрезка,
- 38. Тест: III. Если вектор а имеет координаты {-3; 3; 1}, то его длина равна: 1. 1;
- 39. Тест: IY. Если А(2; 7; 9), В(-2; 7; 1), то расстояние между точками А и В
- 40. Тест: Y. Скалярное произведение векторов а {-4; 3; 0}, в {5; 7; -1} равно: 1. 0;
- 41. Тест: YI. Угол между векторами a {2; -2; 0}, в {3; 0; -3} равен: 1. 90
- 42. Проверка: 3 1 2 3 2 2
- 43. Итог урока: Над какой темой работали? Что повторили?
- 44. Оценка работ: Краснобрыжева И. Мельникова Е. Музалев И. Саблина К. Теряева М. Тужилина О. Ягибеков Р.
- 46. Скачать презентацию








































 Православные переходящие праздники
Православные переходящие праздники Резервы, условные обязательства и условные активы
Резервы, условные обязательства и условные активы 20180113_prezentatsiya_5_klass_chto_takoe_geografiya
20180113_prezentatsiya_5_klass_chto_takoe_geografiya Интеграция и конвергенция методов моделирования в сфере образования при построении системы управления знаниями в области ИКТ
Интеграция и конвергенция методов моделирования в сфере образования при построении системы управления знаниями в области ИКТ Школа методиста. Золотые правила планирования своего рабочего времени
Школа методиста. Золотые правила планирования своего рабочего времени Погост
Погост Землетрясения и вулканы
Землетрясения и вулканы Психология служебной деятельности
Психология служебной деятельности Энергосберегающие фасады от производителя на основе натуральных материалов Tvins Fibro Modern
Энергосберегающие фасады от производителя на основе натуральных материалов Tvins Fibro Modern Детский санаторно-оздоровительный лагерь Шахтинский текстильщик
Детский санаторно-оздоровительный лагерь Шахтинский текстильщик Skara Brae Quiz
Skara Brae Quiz Лига Индиго. Интеллектуально-развлекательная игра. Разрыв шаблона о корпоративных праздниках
Лига Индиго. Интеллектуально-развлекательная игра. Разрыв шаблона о корпоративных праздниках Применение ИКТ на уроках математики
Применение ИКТ на уроках математики ОСОБЕННОСТИ ДЕФЕКТООБРАЗОВАНИЯ ПРИ ВЫРАЩИВАНИИ БЕЗДИСЛОКАЦИОННЫХ МОНОКРИСТАЛЛОВ КРЕМНИЯ И ТЕРМООБРАБОТКЕ ПЛАСТИН
ОСОБЕННОСТИ ДЕФЕКТООБРАЗОВАНИЯ ПРИ ВЫРАЩИВАНИИ БЕЗДИСЛОКАЦИОННЫХ МОНОКРИСТАЛЛОВ КРЕМНИЯ И ТЕРМООБРАБОТКЕ ПЛАСТИН Размещение рекламы на воздушном шаре
Размещение рекламы на воздушном шаре Семейство станций HiPath 1100
Семейство станций HiPath 1100 Техника безопасности на уроках гимнастики
Техника безопасности на уроках гимнастики La mode en France
La mode en France Счётчики посещений. Статистика (03)
Счётчики посещений. Статистика (03) Невербальное общение. Зоны общения
Невербальное общение. Зоны общения Zuckertüte
Zuckertüte Оазец заголовка ПРОФЕССИОНАЛЬНЫЕ ИТ УСЛУГИ Содержание О компании Softline Consulting Services Наши решения Универсальные коммуникации и мобил
Оазец заголовка ПРОФЕССИОНАЛЬНЫЕ ИТ УСЛУГИ Содержание О компании Softline Consulting Services Наши решения Универсальные коммуникации и мобил 1
1 Мой ребенок в детском саду. Фотографии
Мой ребенок в детском саду. Фотографии МОСКОВСКИЙ ГОРОДСКОЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ ФАКУЛЬТЕТ СПЕЦИАЛЬНОЙ ПЕДАГОГИКИ
МОСКОВСКИЙ ГОРОДСКОЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ ФАКУЛЬТЕТ СПЕЦИАЛЬНОЙ ПЕДАГОГИКИ Презентация для проведения занятия по освоению возможностей «е-КМ-Школы» Тема 1: Личный кабинет
Презентация для проведения занятия по освоению возможностей «е-КМ-Школы» Тема 1: Личный кабинет Презентация на тему Тема детства в повести Л.Н.Толстого «Детство»
Презентация на тему Тема детства в повести Л.Н.Толстого «Детство»  Сокращения, принятые в туризме. Теория и практика экскурсионного туризма
Сокращения, принятые в туризме. Теория и практика экскурсионного туризма