Содержание
- 2. КЛЮЧЕВЫЕ ПОНЯТИЯ Процент Дисконтирование Наращение Аннуитет Будущая стоимость Текущая стоимость Ставка дисконта Фактор фонда возмещения Взнос
- 3. Полученная сегодня сумма обладает большей ценностью, чем ее эквивалент, полученный в будущем. Будущие поступления менее ценны,
- 4. Основные понятия теории стоимости денег во времени процент - это доход от предоставления денег в долг
- 5. Основные понятия теории стоимости денег во времени капитализация процента - присоединение начисленных процентов к основной сумме;
- 6. Условные обозначения: I – проценты за весь срок ссуды (interest); PV – первоначальная сумма долга или
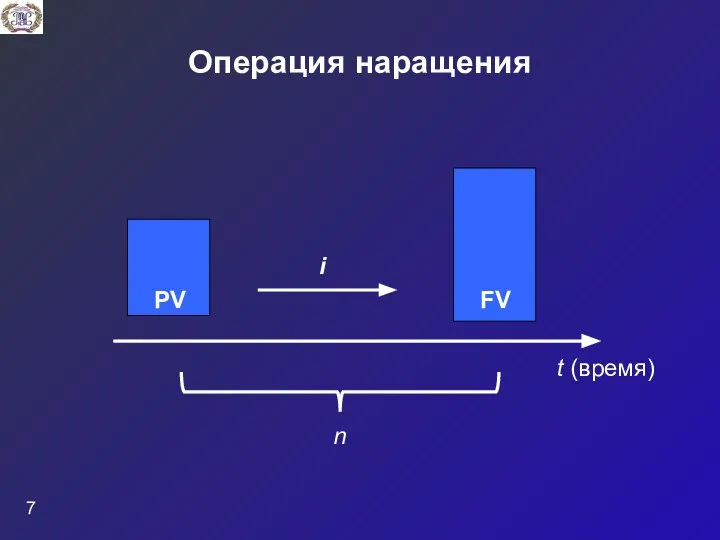
- 7. Операция наращения PV FV i t (время) n
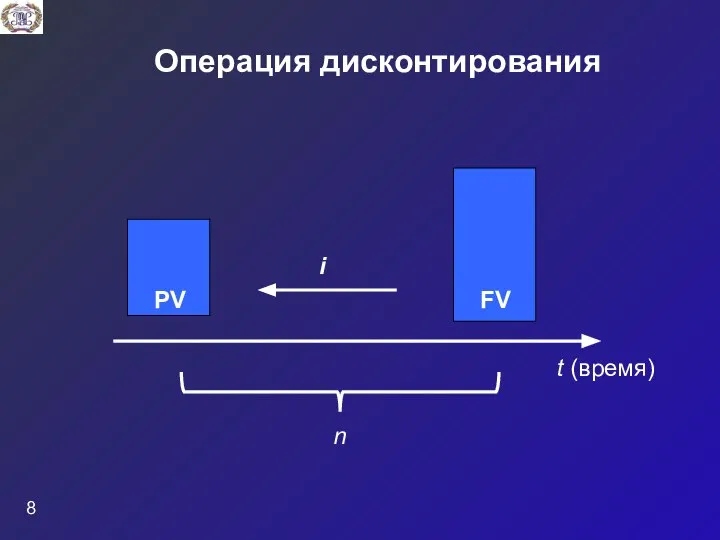
- 8. Операция дисконтирования PV FV i t (время) n
- 9. В зависимости от базы для начисления процента различают: Простой процент Сложный процент
- 10. Формула простых процентов FV = PV + I = PV + i • PV • n
- 11. Применение схемы сложных процентов целесообразно в тех случаях, когда: Срок ссуды более года. Проценты не выплачиваются
- 12. Формула сложных процентов FV = PV • (1 + i)n , где FV – наращенная сумма
- 13. Номинальная ставка (nominal rate) – годовая ставка процентов, исходя из которой определяется величина ставки процентов в
- 14. Эффективная ставка (effective rate), измеряет тот реальный относительный доход, который получен в целом за год, с
- 15. Сущность потока платежей Ряд распределенных во времени выплат и поступлений называется потоком платежей. Поток платежей, все
- 16. Обобщающие характеристики финансовых потоков Наращенная сумма. Текущая стоимость потока платежей.
- 17. Наращенная сумма Сумма всех платежей с начисленными на них процентами к концу срока ренты. Это может
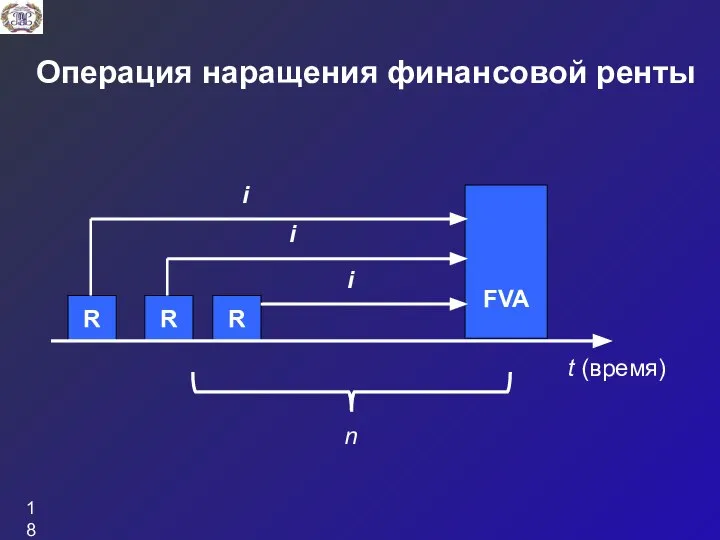
- 18. Операция наращения финансовой ренты FVA t (время) n
- 19. Определение наращенной суммы для годовой постоянной обычной ренты где FVA – наращенная сумма ренты; R –
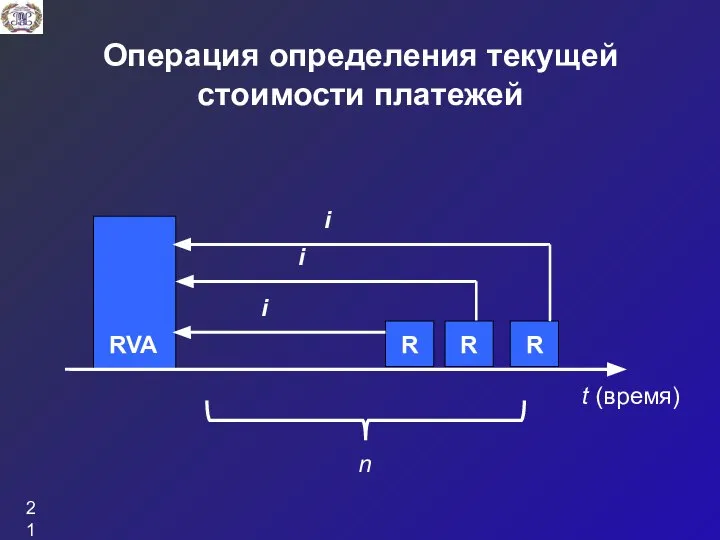
- 20. Современная (текущая) величина потока платежей (капитализированная или приведенная величина) – это сумма платежей, дисконтированных на момент
- 21. Операция определения текущей стоимости платежей t (время) n
- 22. Годовая обычная рента В простейшем случае, для годовой обычной ренты с выплатами в конце каждого года,
- 23. Величина годовой и срочной ренты Годовая рента с начислением процентов несколько раз в год: Срочная рента
- 24. Текущая величина ренты Срочная рента с неоднократным начислением процентов в течение года, при условии, что число
- 25. Величина рентного платежа Если сумма долга определена на какой-либо момент в будущем (FVA), тогда величину последующих
- 26. Величина рентного платежа Если исходной величиной является текущая стоимость финансовой ренты, тогда, исходя из ставки процента
- 28. Скачать презентацию





















 Трудовые правоотношения Трудовое право как отрасль российского права. Правовое регулирование трудовых отношений
Трудовые правоотношения Трудовое право как отрасль российского права. Правовое регулирование трудовых отношений Самостоятельное участие несовершеннолетних в возрасте от 14 до 18 лет в гражданском процессе
Самостоятельное участие несовершеннолетних в возрасте от 14 до 18 лет в гражданском процессе Использование сайта учителя как условие повышения качества обучения мотивированных учащихся
Использование сайта учителя как условие повышения качества обучения мотивированных учащихся Participe passe
Participe passe Восприятие. Виды восприятия
Восприятие. Виды восприятия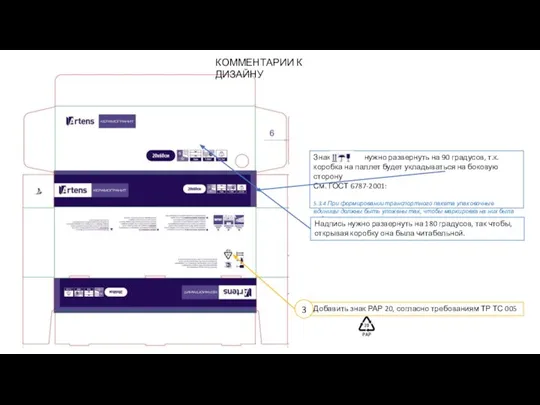 PCS-1609_06_ARTENS плитка%2c комментарии к коробу пицца
PCS-1609_06_ARTENS плитка%2c комментарии к коробу пицца Презентация на тему Книжная миниатюра Востока
Презентация на тему Книжная миниатюра Востока Наша эмблема
Наша эмблема Евгений Пермяк1902-1982
Евгений Пермяк1902-1982 Презентация Социал-Дарвинизм Галлямов Артур
Презентация Социал-Дарвинизм Галлямов Артур Приобретенные формы поведения
Приобретенные формы поведения Мой современник. АНО ДО Параллели
Мой современник. АНО ДО Параллели Особенности реализации требований СТО БР ИББС по защите персональных данных
Особенности реализации требований СТО БР ИББС по защите персональных данных Международные экономические отношения
Международные экономические отношения Мое будущее в профессии психолога
Мое будущее в профессии психолога Лекция 5. “ Риск банкротства как основное проявление финансовых рисков”
Лекция 5. “ Риск банкротства как основное проявление финансовых рисков” Великое русское слово
Великое русское слово «Никто не может достичь совершенства в каратэ-до до тех пор, пока не осознает, что каратэ-до есть ещё и вера в жизненный путь»
«Никто не может достичь совершенства в каратэ-до до тех пор, пока не осознает, что каратэ-до есть ещё и вера в жизненный путь» Новософт
Новософт Право, его формы и структура. Продолжение
Право, его формы и структура. Продолжение Курс Онлайн-философия. Уральский федеральный университет
Курс Онлайн-философия. Уральский федеральный университет «Пожар!»педагогический проект
«Пожар!»педагогический проект Круг чтения
Круг чтения Расчет мгновенных схем на однопутных участках постоянного тока при двустороннем питании
Расчет мгновенных схем на однопутных участках постоянного тока при двустороннем питании Анализ характеристик многослойного образца и синтез многомерного оператора
Анализ характеристик многослойного образца и синтез многомерного оператора Зима
Зима Педагогическое образование. Профили Технология и Экономика
Педагогическое образование. Профили Технология и Экономика