Прямоугольник

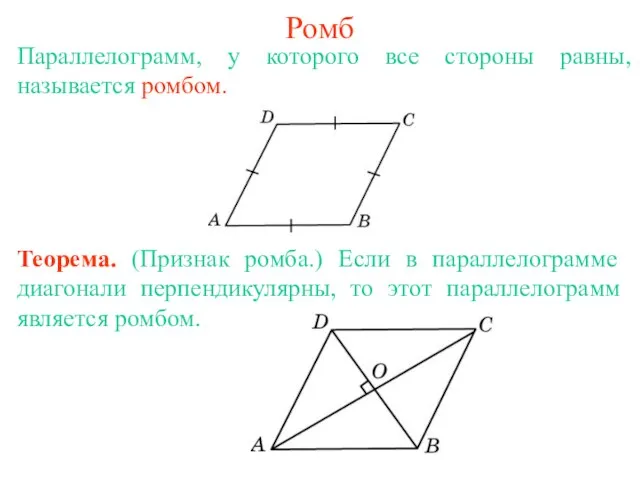
Ромб
Параллелограмм, у которого все стороны равны, называется ромбом.

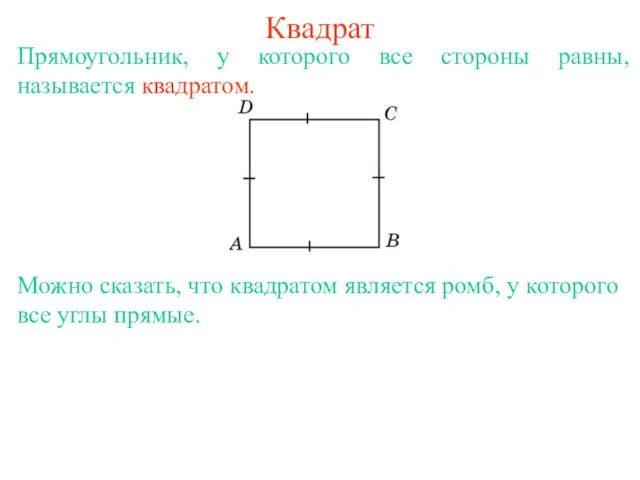
Квадрат
Прямоугольник, у которого все стороны равны, называется квадратом.
Можно сказать, что квадратом является ромб, у которого все углы прямые.

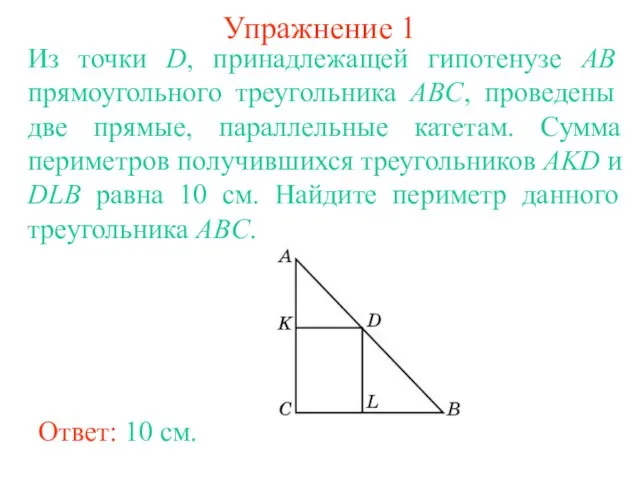
Упражнение 1
Из точки D, принадлежащей гипотенузе AB прямоугольного треугольника ABC, проведены две прямые, параллельные катетам. Сумма периметров получившихся треугольников AKD и DLB равна 10 см. Найдите периметр данного треугольника ABC.
Ответ: 10 см.

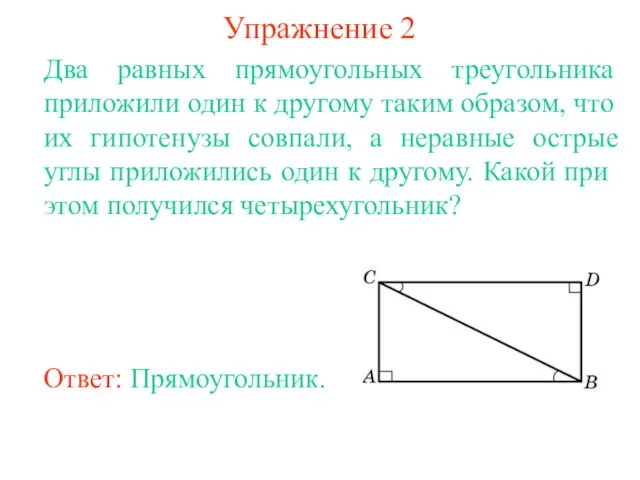
Упражнение 2
Два равных прямоугольных треугольника приложили один к другому таким образом, что их гипотенузы совпали, а неравные острые углы приложились один к другому. Какой при этом получился четырехугольник?

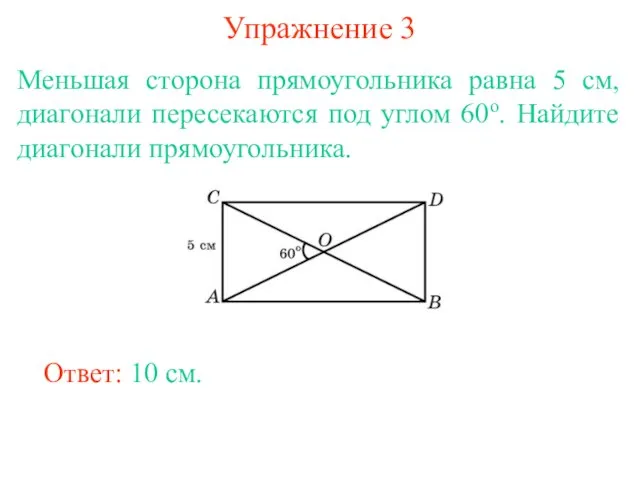
Упражнение 3
Меньшая сторона прямоугольника равна 5 см, диагонали пересекаются под углом 60о. Найдите диагонали прямоугольника.
Ответ: 10 см.

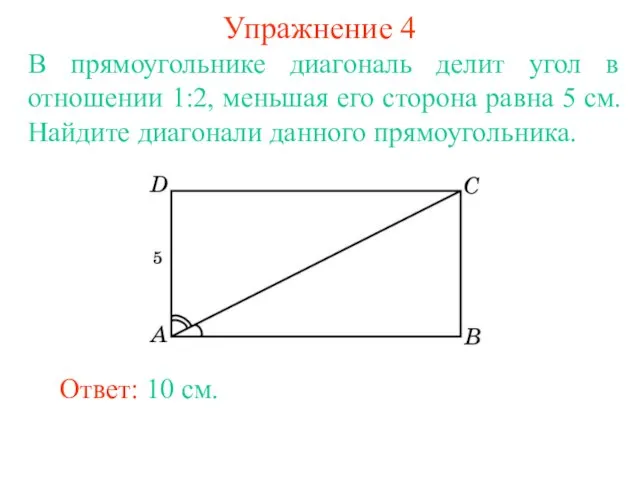
Упражнение 4
В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 5 см. Найдите диагонали данного прямоугольника.
Ответ: 10 см.

Упражнение 5
Диагональ прямоугольника вдвое больше одной из его сторон. Какие углы образуют диагонали со сторонами прямоугольника?
Ответ: 30о и 60о.

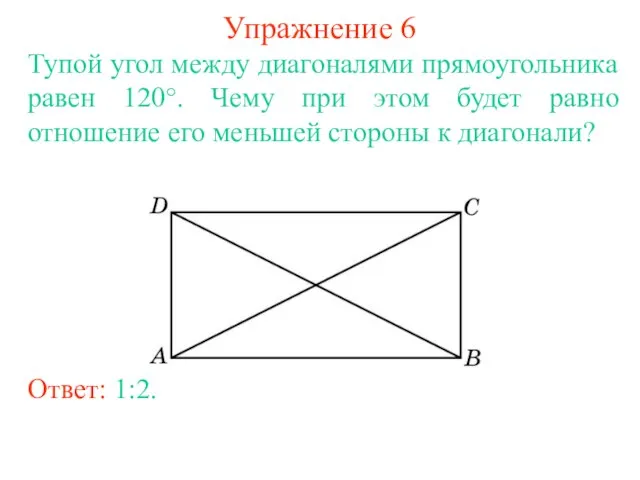
Упражнение 6
Тупой угол между диагоналями прямоугольника равен 120°. Чему при этом будет равно отношение его меньшей стороны к диагонали?
Ответ: 1:2.

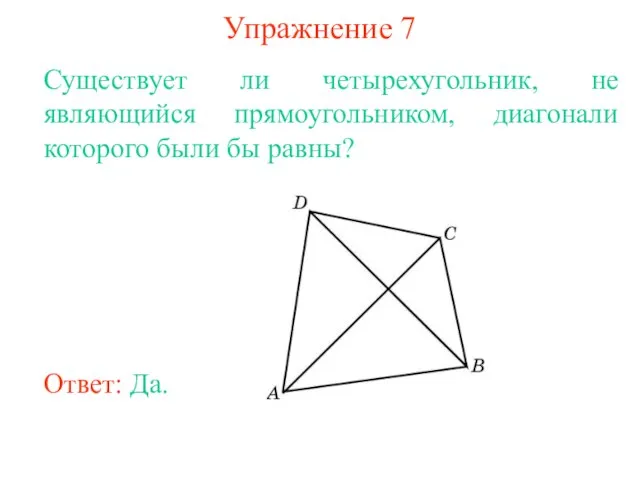
Упражнение 7
Существует ли четырехугольник, не являющийся прямоугольником, диагонали которого были бы равны?

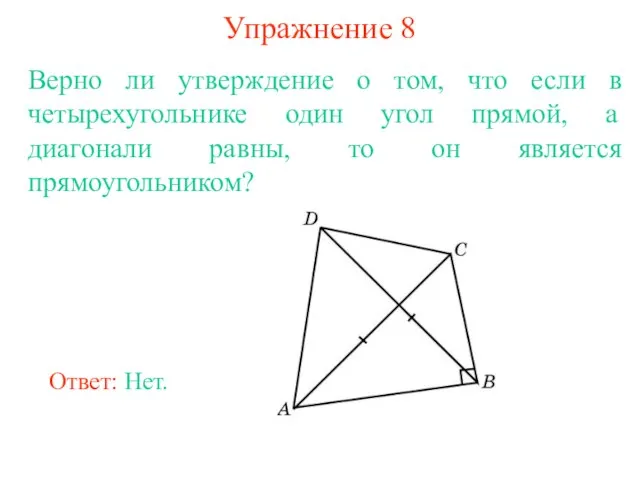
Упражнение 8
Верно ли утверждение о том, что если в четырехугольнике один угол прямой, а диагонали равны, то он является прямоугольником?

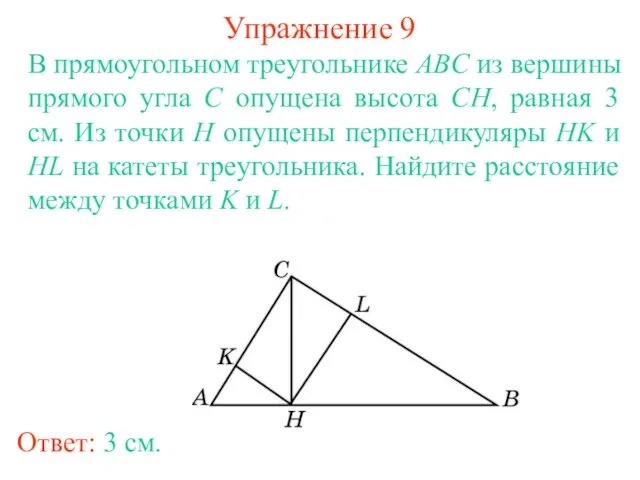
Упражнение 9
В прямоугольном треугольнике ABC из вершины прямого угла C опущена высота CH, равная 3 см. Из точки H опущены перпендикуляры HK и HL на катеты треугольника. Найдите расстояние между точками K и L.
Ответ: 3 см.

Упражнение 10
Найдите диагонали прямоугольника, если его периметр равен 34 см, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен 30 см.
Ответ: 13 см.

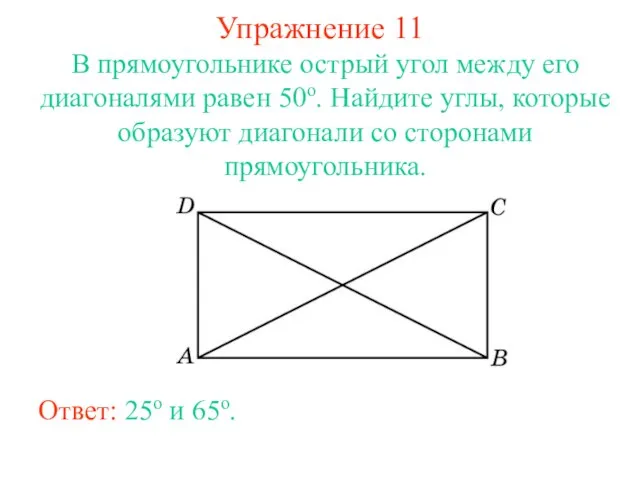
Упражнение 11
В прямоугольнике острый угол между его диагоналями равен 50о. Найдите углы, которые образуют диагонали со сторонами прямоугольника.
Ответ: 25о и 65о.

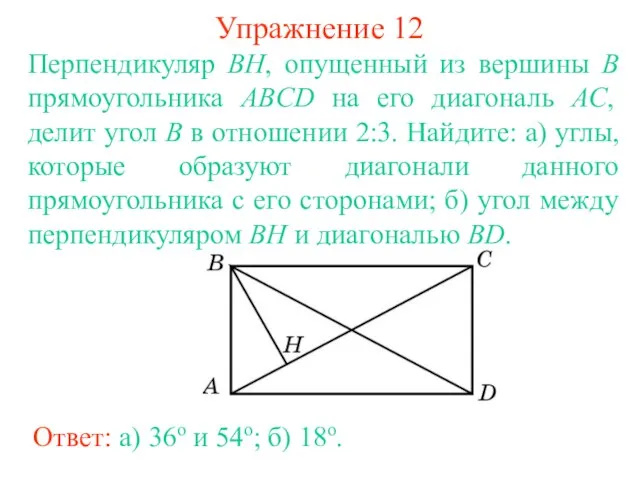
Упражнение 12
Перпендикуляр BH, опущенный из вершины B прямоугольника ABCD на его диагональ AC, делит угол B в отношении 2:3. Найдите: а) углы, которые образуют диагонали данного прямоугольника с его сторонами; б) угол между перпендикуляром BH и диагональю BD.
Ответ: а) 36о и 54о;
б) 18о.

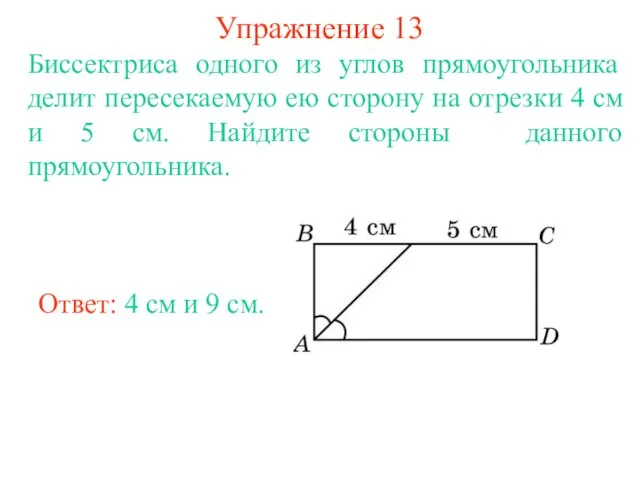
Упражнение 13
Биссектриса одного из углов прямоугольника делит пересекаемую ею сторону на отрезки 4 см и 5 см. Найдите стороны данного прямоугольника.

Упражнение 14
Чему равна меньшая диагональ ромба со стороной а и острым углом в 60о?
Ответ: a.

Упражнение 15
В ромбе одна из диагоналей равна его стороне. Найдите углы ромба.
Ответ: 60o, 120o, 60o, 120o.

Упражнение 16
Углы, образуемые диагоналями ромба с одной из его сторон, относятся как 4:5. Найдите углы ромба.
Ответ: 80o, 100o, 80o, 100o.

Упражнение 17
Чему равен угол между: а) диагоналями квадрата: б) диагональю и стороной квадрата?
Ответ: а) 90o;
б) 45o.