Содержание
- 2. Содержание Введение Глава I Глава II Список используемой литературы Приложение
- 3. Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной
- 4. Золотое сечение – гармоническая пропорция. Золотое сечение – это такое пропорциональное деление отрезка на неравные части,
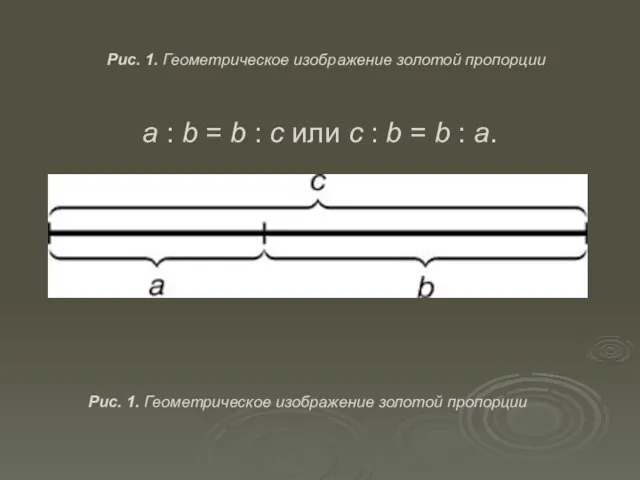
- 5. Рис. 1. Геометрическое изображение золотой пропорции a : b = b : c или с :
- 6. Деление отрезка прямой по золотому сечению Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка
- 8. Свойства золотого сечения описываются уравнением: x2 – x – 1 = 0. Решение этого уравнения: Свойства
- 9. Золотой треугольник Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и
- 11. Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через
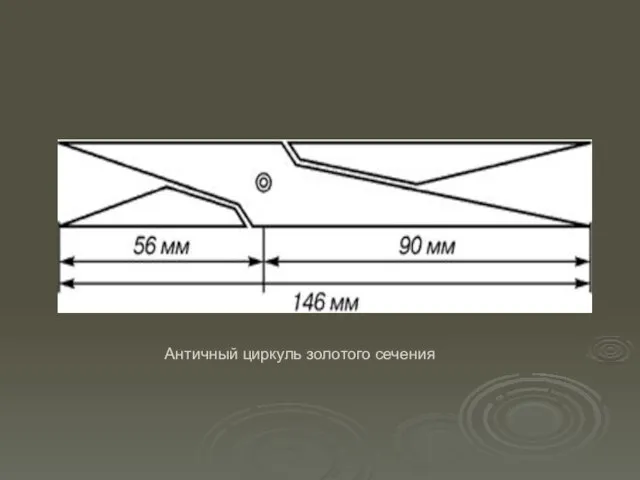
- 13. Античный циркуль золотого сечения
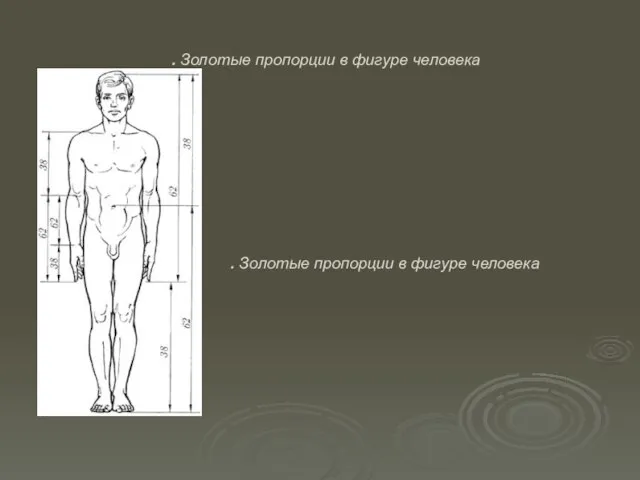
- 14. . Золотые пропорции в фигуре человека . Золотые пропорции в фигуре человека
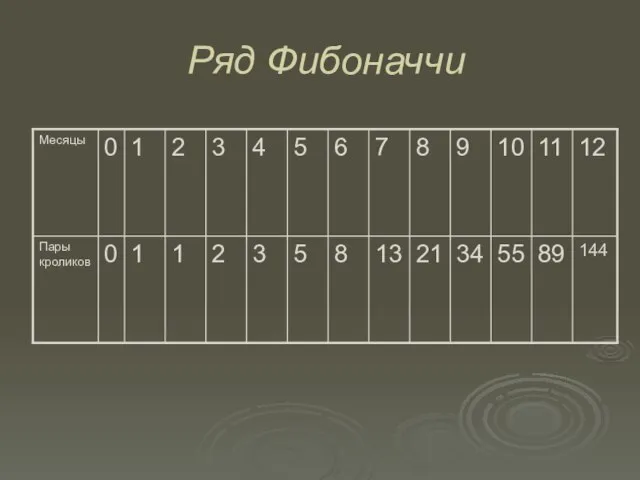
- 15. Ряд Фибоначчи
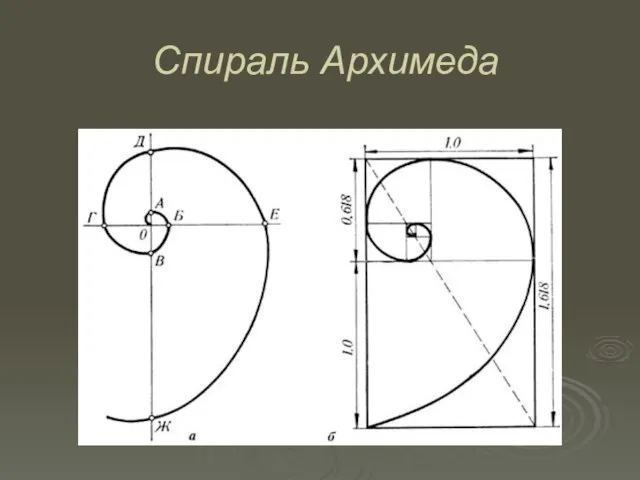
- 16. Спираль Архимеда
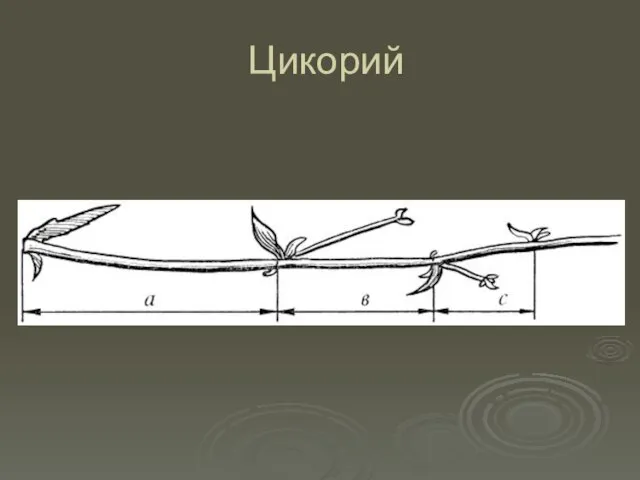
- 17. Цикорий
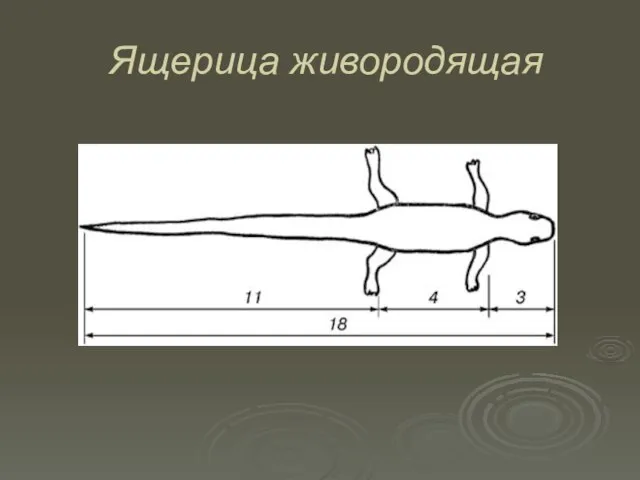
- 18. Ящерица живородящая
- 19. . Список используемой литературы. Ковалев Ф.В. Золотое сечение в живописи. К.: Высшая школа, 1989. Кеплер И.
- 20. «Золотое сечение» в скульптуре
- 21. «Золотое сечение» в архитектуре
- 22. «Золотое сечение» в живописи
- 23. Задача. Дан треугольник ABC. Точки P и Q лежат на сторонах AB и AC соответственно, Т-точка
- 28. Скачать презентацию


















 Изображения изделий и их обозначения при выполнении графических конструкторских документов
Изображения изделий и их обозначения при выполнении графических конструкторских документов Использование функций
Использование функций Математические задачи от русских, советских и зарубежных писателей
Математические задачи от русских, советских и зарубежных писателей Каникулы в международном детском лагере
Каникулы в международном детском лагере Язык есть исповедь народа
Язык есть исповедь народа Работа по стимулированию юридических лиц и индивидуальных предпринимателей к трудоустройству безработных
Работа по стимулированию юридических лиц и индивидуальных предпринимателей к трудоустройству безработных Физико-географическое районирование Северной Евразии
Физико-географическое районирование Северной Евразии  Узоры “тетёрки ” на печенье
Узоры “тетёрки ” на печенье Презентация на тему Постоянные магниты
Презентация на тему Постоянные магниты Весенний фестиваль для учащихся
Весенний фестиваль для учащихся 23 февраля. Поздравляем!
23 февраля. Поздравляем! Российский государственный университет нефти и газа имени И.М.Губкина Кафедра машин и оборудования нефтяной и газовой промышленн
Российский государственный университет нефти и газа имени И.М.Губкина Кафедра машин и оборудования нефтяной и газовой промышленн Звук и свет в лирике И. Анненского
Звук и свет в лирике И. Анненского Книжка-раскраска
Книжка-раскраска Взаимодействие научного руководителя со студентами через личный кабинет с использование сервиса Антиплагиат
Взаимодействие научного руководителя со студентами через личный кабинет с использование сервиса Антиплагиат Зачем живые организмы запасают питательные вещества?
Зачем живые организмы запасают питательные вещества? Особенности приема 2020 (колледж). Дистанционная подача документов
Особенности приема 2020 (колледж). Дистанционная подача документов Ресурсный Центр «Кристина»
Ресурсный Центр «Кристина» Проверка правильности кирпичной кладки
Проверка правильности кирпичной кладки Смешанное обучение – blended learning
Смешанное обучение – blended learning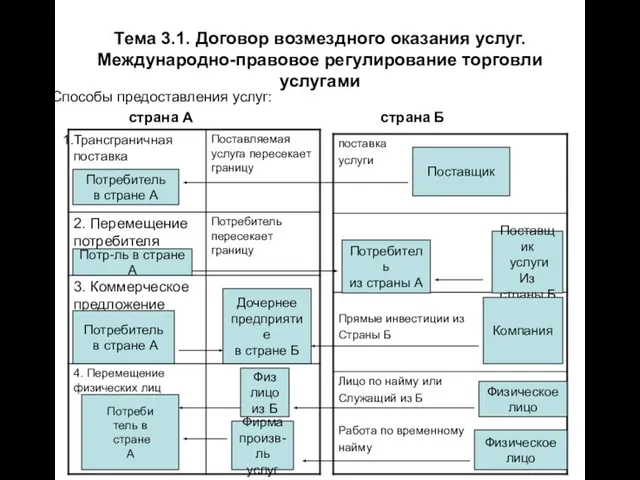 Тема 3.1. Договор возмездного оказания услуг. Международно-правовое регулирование торговли услугами Способы предоставления услуг
Тема 3.1. Договор возмездного оказания услуг. Международно-правовое регулирование торговли услугами Способы предоставления услуг Конвенция о правах ребенка
Конвенция о правах ребенка Богомолова Роза Александровна
Богомолова Роза Александровна Renault Assistance. Служба маркетинга запасных частей и послепродажного обслуживания
Renault Assistance. Служба маркетинга запасных частей и послепродажного обслуживания Принцип действия жидкокристаллических дисплеев
Принцип действия жидкокристаллических дисплеев Правила работы с обучающей презентацией
Правила работы с обучающей презентацией плакат
плакат ОП по Гагинскому району МО МВД России Большеболдинский: история, сегодняшнее состояние и перспективы развития
ОП по Гагинскому району МО МВД России Большеболдинский: история, сегодняшнее состояние и перспективы развития