Работа с массивами ВЕКТОРЫ И МАТРИЦЫ

Объявление массивов
Массивы с фиксированными границами
Option Base 1
Dim a! ( 5 ), B% ( 6, 8 ), C!( 3, 5, 9 )
Динамическое описание массивов
Dim a! (), B% ()
n= InputBox (“n=”)
m= InputBox (“m=”)
k= InputBox (“k=”)
Redim a ( n ), B ( m,k )

Вектор
С упорядоченной последовательностью действительных чисел a1,a2,a3,…,an-1,an можно связать понятие связанного вектора в n-мерном пространстве и обозначить как:
или понятие точки A(a1,a2,a3,…,an). Числа a1,a2,a3,…,an называются координатами точки A
или элементами вектора , а количество элементов в векторе называется размерностью этого вектора. Положение элемента ai определяется индексом i, где i = 1,2,· ··,n. Компоненты вектора записываются в виде столбца.

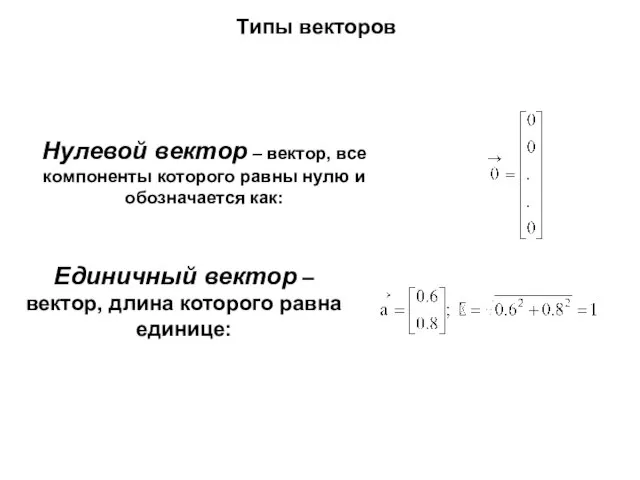
Типы векторов
Нулевой вектор – вектор, все компоненты которого равны нулю и обозначается как:
Единичный вектор – вектор, длина которого равна единице:

Матрица
Совокупность чисел расположенных в прямоугольной таблице, состоящей из n строк и m столбцов, называется матрицей и обозначается как:
Положение элемента в матрице определяется двумя индексами (i , j), где i определяет номер строки , j – номер столбца .
a (i , j )

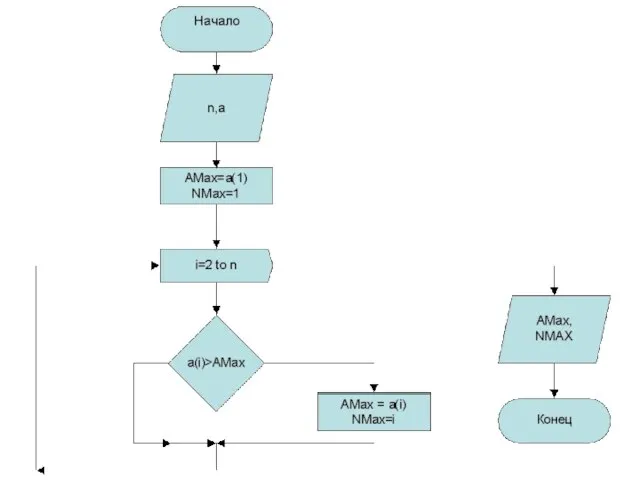
Примеры программ
Задача 1. В одномерном массиве а(n) найти максимальный по значению элемент и указать его номер

Программа к задаче 1
Sub vektmax ()
Dim a!(), n%, i%, NMax%, AMax!
n=InputBox(“n=“)
Redim a(n)
Rem Ввод элементов вектора
For i=1 to n
a(i)=InputBox(“Введи а(i)”)
next i

Продолжение к программе1
Rem поиск АMах, NMax
Amax=a(1): NMax=1
For i=2 to n
if a(i) >Amax then
AMax=a(i)
NMax=i
end if
Next i
Rem вывод значений
msgBox (“NMax=“)&NMax
msgBox (“AMax=“)&Amax
End sub

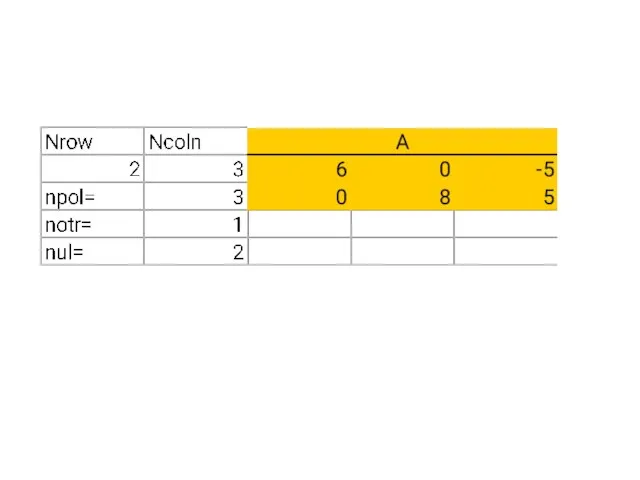
Задача 2.
В двумерном массиве A (nrow, ncoln) подсчитать количество положительных, отрицательных и нулевых элементов.

Выбор идентификаторов для переменных и их типов
A! ( nrow%, ncoln% )
npol %, notr %, nnul %
j %, i % -рабочие переменные

Sub matr()
Dim A!(), nrow%, i%
Dim ncoln%, j %
Dim npol%, notr %, nnul %
nrow = Cells (2, 1)
ncoln = Cells (2, 2)
ReDim A( nrow, ncoln )
For i = 1 To nrow
For j = 1 To ncoln
A(i, j) = Cells (i + 1, j + 2)
Next j
Next i
npol = 0: notr = 0:
nnul = 0
For i = 1 To nrow
For j = 1 To ncoln
If A(i, j) > 0 Then
npol = npol + 1
ElseIf A(i, j) = 0 Then
nnul = nnul + 1
Else
notr = notr + 1
End If
Next j
Next i
Cells(3, 2) = npol
Cells(4, 2) = notr
Cells(5, 2) = nnul
End Sub

1.Важнейшие характеристики вектора (3 способа вычисления нормы).
2.Действия над векторами
-равенство
-сложение
-умножение вектора на скаляр
-транспонирование вектора
-скалярное произведение векторов, вычисление угла между векторами

Норма вектора (Евклидова)
Норма (длина) вектора
Пример.

Function NVec ! ( Nrow%, a!())
Dim s As Single
Dim i As Integer
s = 0
For i = 1 to Nrow
s = s + a(i) * a(i)
Next i
NVec = sqr(s)
End Function
Исполняемая процедура (main)
Option base 1
Sub NormVector ()
Dim n %, a ! ()
Dim i %
n = Cells(2, 1)
Redim a(n)
For i= 1 to n
a(i) = Cells(i + 3, 1)
Next i
Cells(2, 3) = NVec(n,a)
End Sub
Вызываемая функция

Нормы вектора для ручного счета
на первом курсе это сложно

Складывать или вычитать можно только вектора с одинаковой размерностью.
Сложение и вычитание векторов.

Option base 1
Sub AddVector()
Dim n%, a!(), b!(), c!()
Dim i As Integer
n=Cells(2,1)
Redim a(n), b(n), c(n)
For i = 1 to n
a(i)=Cells(3 + i, 1)
b(i)=Cells(3 + i, 2)
Next i
Call AddV (n,a,b,c)
For i= 1 to n
Cells(3 + i, 3)=c(i)
Next i
End Sub
Исполняемая процедура (main)
Sub AddV ( Nrow%, a!(), b!(),r!())
Dim i As Integer
For i = 1 to Nrow
r(i) = a(i) + b(i)
next i
End Sub
Вызываемая процедура

Умножение вектора на константу.

Это изменения представления вектора. Замена столбца на строку.
Транспонирование вектора

Это значение суммы произведений соответствующих компонент двух векторов.
Скалярное произведение векторов
Вызываемая функция
Пример
Function Scal (Nrow %, a !() , b ! ()) As Single
Dim i As Integer, s As Single
s = 0
For i = 1 to Nrow
s = s + a(i) * b(i)
Next i
Scal = s
End Function

Матрица
Совокупность чисел расположенных в прямоугольной таблице, состоящей из n строк и m столбцов, называется матрицей и обозначается как:
Положение элемента в матрице определяется двумя индексами (i , j), где i определяет номер строки , j – номер столбца .
a (i , j )

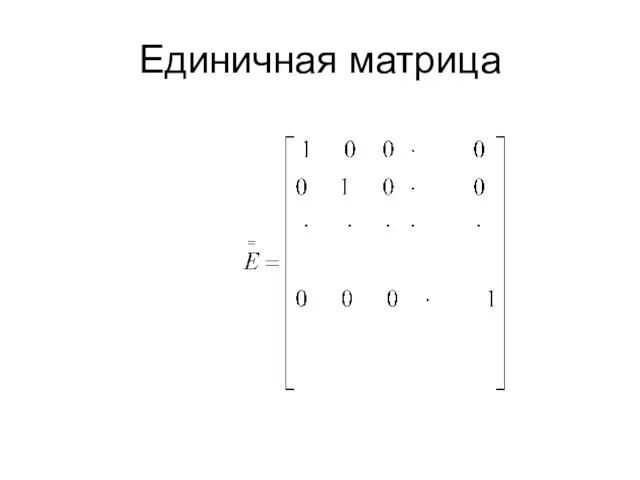
Единичная матрица

Норма матрицы (Эвклидова).

Option base 1
Sub NormaMatrix()
Dim n%, m%, a!()
Dim i As Integer, j %, s !
n=Cells(2, 1)
m= Cells(2, 2)
Redim a(n,m)
For i = 1 to n
For j = 1 to m
a(i, j) = Cells(3 + i, j)
Next j
Next i
Cells(2, 3) = NormM(n,m,a)
End Sub
Исполняемая процедура (main)
Function NormM(Nrow%, Ncol%, A!())
Dim i As Integer, j As Integer
Dim s As Single
s = 0
For i = 1 to Nrow
For j = 1 to Ncol
s = s + A(i, j)^2
Next j
Next i
NormM = sqr(s)
End Function
Вызываемая функция

Складывать или вычитать можно только матрицы с одинаковой размерностью. A(n,m), B(n,m). C(n,m) матрица результата
Сложение и вычитание матриц.
Sub AddM(Nrow %, Ncol % A ! () , B ! () , C ! () )
Dim i As Integer, j As Integer
For i = 1 to Nrow
For j = 1 to Ncol
C(i, j) = A(i, j) + B(i, j)
Next j
Next i
End Sub
Вызываемая процедура

Умножение матрицы на константу.