Содержание
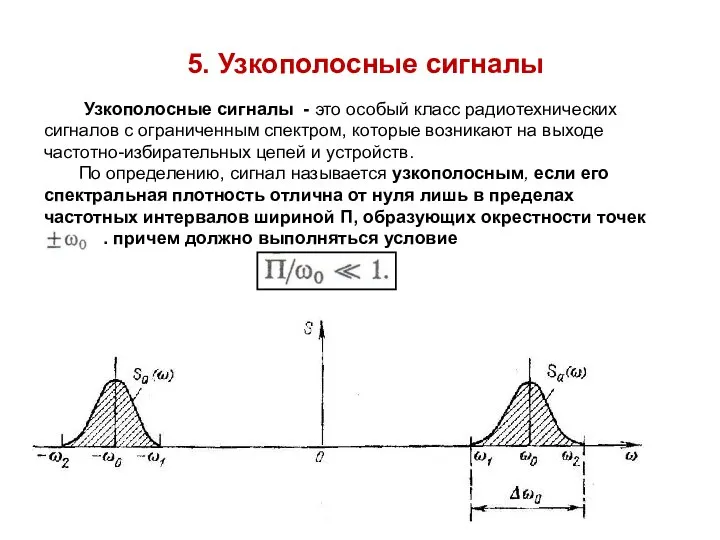
- 2. 5. Узкополосные сигналы Узкополосные сигналы - это особый класс радиотехнических сигналов с ограниченным спектром, которые возникают
- 3. 5.1. Математическая модель узкополосного сигнала Если / — низкочастотный сигнал, спектр которого сосредоточен в окрестности нулевой
- 4. Выделение квадратурных составляющих узкополосного сигнала Синфазную и квадратурную амплитуды можно выделить аппаратурным способом. Действительно, пусть имеется
- 5. Независящее от времени число называют комплексной амплитудой гармонического колебания. С физической точки зрения узкополосные сигналы представляют
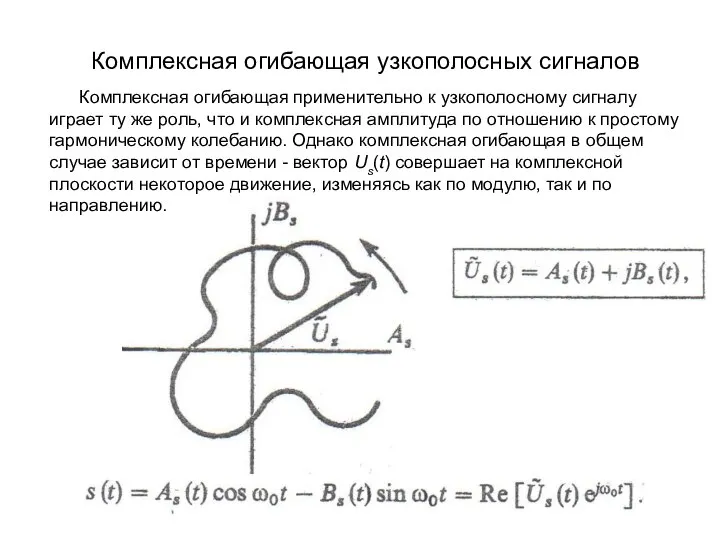
- 6. Комплексная огибающая узкополосных сигналов Комплексная огибающая применительно к узкополосному сигналу играет ту же роль, что и
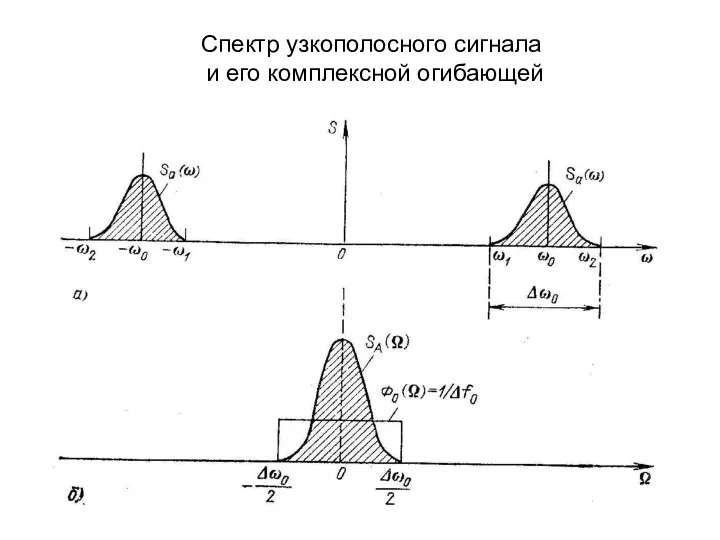
- 7. Спектр узкополосного сигнала и его комплексной огибающей
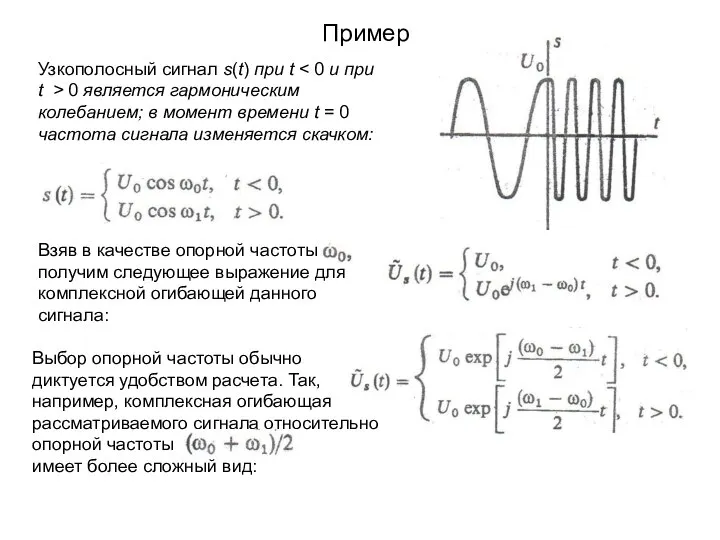
- 8. Пример Узкополосный сигнал s(t) при t t > 0 является гармоническим колебанием; в момент времени t
- 9. 5.3. Физическая огибающая, полная фаза и мгновенная частота Определим комплексную огибающую в показательной форме:. Здесь Us(t)
- 10. Свойства физической огибающей узкополосного сигнала 1. Определим физическую огибающую Us(t) через синфазную и квадратурную амплитуды: 2.
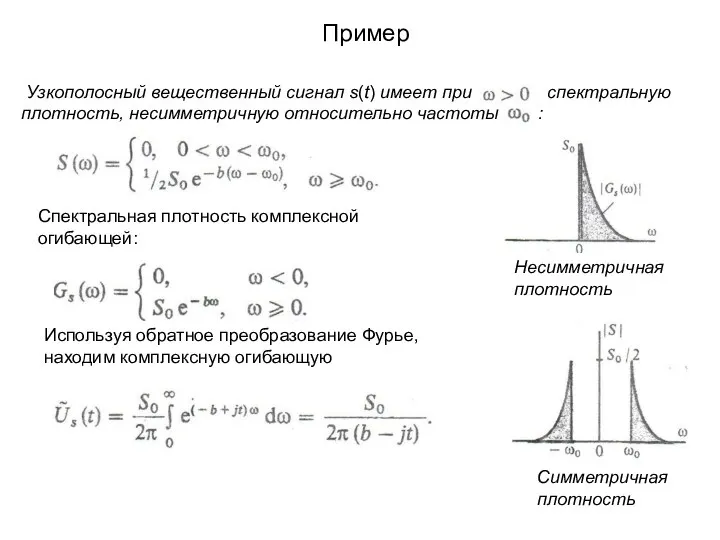
- 11. Пример Узкополосный вещественный сигнал s(t) имеет при спектральную плотность, несимметричную относительно частоты : Спектральная плотность комплексной
- 12. Пример (продолжение) Синфазную и квадратурную амплитуды вещественного сигнала найдем, выделив вещественную и мнимую части: Физическая огибающая
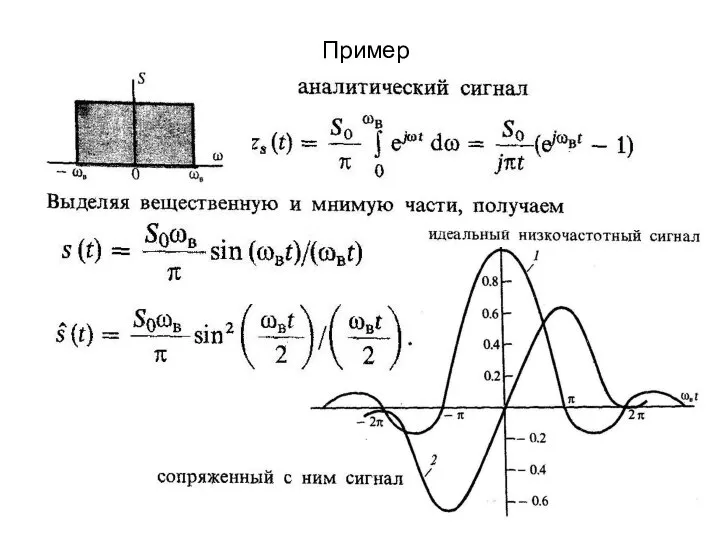
- 13. 5.4. Аналитический сигнал
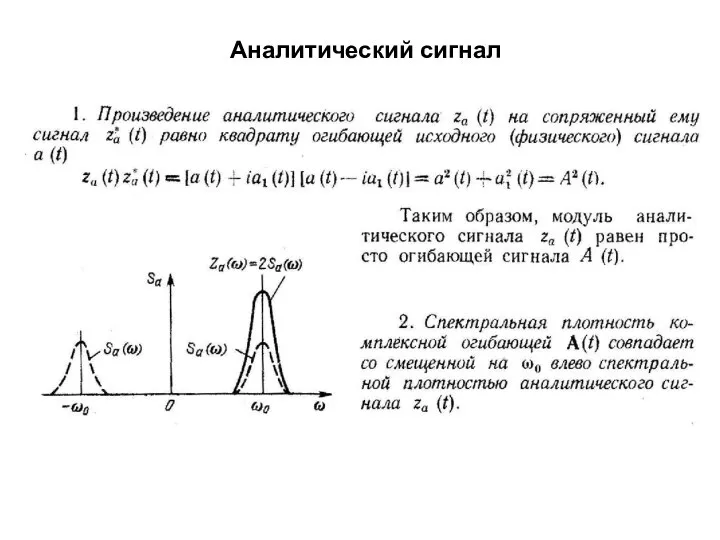
- 14. Аналитический сигнал
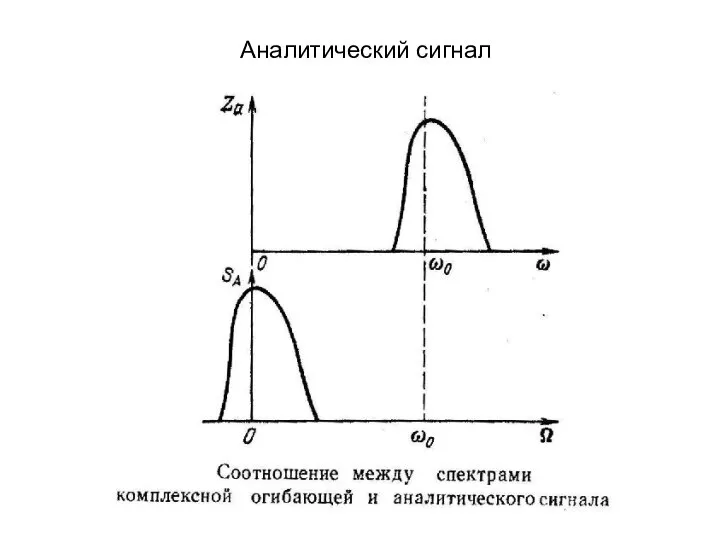
- 15. Аналитический сигнал
- 16. Определение частоты по исходному и сопряжённому сигналам
- 17. Аналитический сигнал
- 18. 5.5. Аналитический сигнал узкополосного процесса
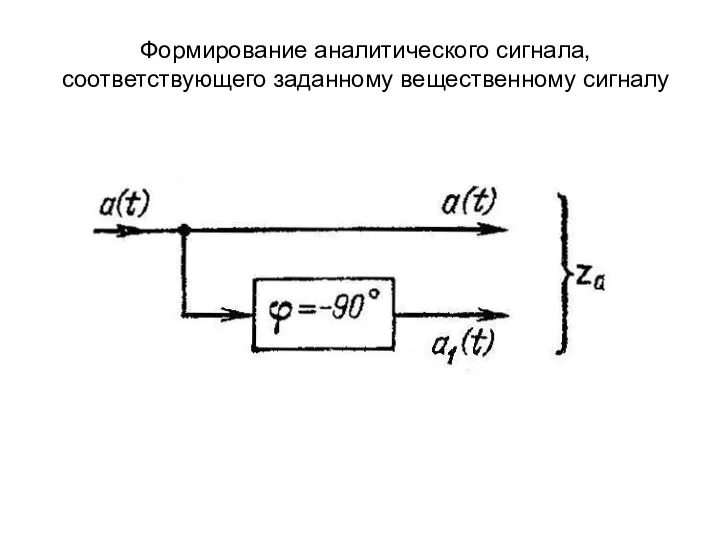
- 19. Формирование аналитического сигнала, соответствующего заданному вещественному сигналу
- 20. Пример
- 21. 5.6. Корреляционная функция аналитического сигнала
- 22. 5.7. Дискретизация узкополосного сигнала
- 24. Скачать презентацию












 Society and Social Interaction
Society and Social Interaction Скифы 11 класс
Скифы 11 класс Конфликтогены и техники профилактики конфликтов
Конфликтогены и техники профилактики конфликтов Дети Великой Отечественной войны
Дети Великой Отечественной войны Освоение углеводородных ресурсов полуострова Ямал
Освоение углеводородных ресурсов полуострова Ямал Использование инновационных технологий в обучении химии
Использование инновационных технологий в обучении химии Стихи и песни о Великой Отечественной войне
Стихи и песни о Великой Отечественной войне Критерии оценивания проектной деятельности и презентаций
Критерии оценивания проектной деятельности и презентаций Предмет и метод учебного курса Законодательная техника
Предмет и метод учебного курса Законодательная техника СЕМЕН ЗАХАРЫЧ МАРМЕЛАДОВ
СЕМЕН ЗАХАРЫЧ МАРМЕЛАДОВ Презентация на тему Индустриальная революции
Презентация на тему Индустриальная революции 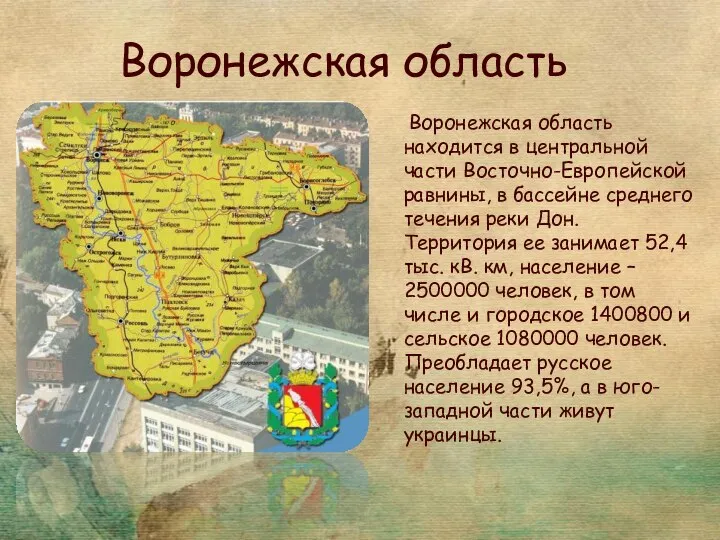 Воронежская область
Воронежская область ВИНО 1 часть
ВИНО 1 часть Отчет о реализации плана мероприятий Правительства Тверской области
Отчет о реализации плана мероприятий Правительства Тверской области Биология - совокупность наук о живом…
Биология - совокупность наук о живом… Бизнес-план проекта творческого развития детей SitPlay
Бизнес-план проекта творческого развития детей SitPlay Координационный совет по организации отдыха, оздоровления и занятости детей
Координационный совет по организации отдыха, оздоровления и занятости детей Презентация на тему Виды жилых помещений
Презентация на тему Виды жилых помещений  Present Simple
Present Simple  Коммерческое предложение по Генеральному спонсорству проекта «X Фактор» в эфире телеканала «Первый Канал «Евразия»
Коммерческое предложение по Генеральному спонсорству проекта «X Фактор» в эфире телеканала «Первый Канал «Евразия» История утюга. Параметры Braun TexStyle 7 TS 785 STP
История утюга. Параметры Braun TexStyle 7 TS 785 STP Стратегии
Стратегии С Прощёным воскресеньем, дорогие читатели!
С Прощёным воскресеньем, дорогие читатели! Time-менеджмент для управления своей жизнью
Time-менеджмент для управления своей жизнью Славный народ - собаки
Славный народ - собаки Использование национально-регионального компонента в обучении химии на элективных курсах
Использование национально-регионального компонента в обучении химии на элективных курсах Социальное государство. Задания для выполнения
Социальное государство. Задания для выполнения Лидия Алексеевна Чарская
Лидия Алексеевна Чарская