Содержание
- 2. Человеку, изучающему алгебру, часто полезнее решить одну задачу тремя различными способами, чем решать три-четыре различные задачи.
- 3. Урок одной задачи Различные способы решения квадратных уравнений
- 4. Цели: - систематизировать различные способы решения квадратных уравнений, дать представление учащимся о важных вехах истории развития
- 5. Методы решения квадратных уравнений были известны ещё в давние времена. Их умели решать вавилоняне ( около
- 6. В трудах древнегреческого математика Евклида и многих математиков древности квадратные уравнения решались геометрическим способом Евклид
- 7. Для решения квадратных уравнений поступали следующим образом. х 2+10х =39 Пусть АВ =х, ВС=5, (10:2) АС=АВ+ВС
- 8. Аль - Хорезми В трактате «Китаб аль-джебр валь-мукабала» хорезмский математик разъяснил приёмы решения уравнений ах2 =
- 9. Так решал эту же задачу ал-Хорезми в 825году Строим квадрат со стороной х и на его
- 10. Древнегреческий математик Диофант 3 век нашей эры Пусть сумма двух чисел 20, а произведение 96. Предположим
- 11. М. Штифель (1487-1567) Общее правило решения квадратных уравнений, приведённых к виду х2 +bx = c, было
- 12. Франсуа Виет(1540-1603) Именно этим французским математиком впервые были введены буквенные обозначения. До этого пользовались громоздкими словесными
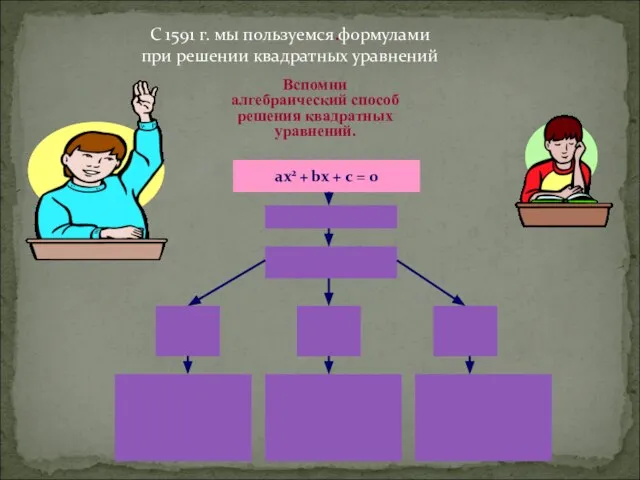
- 13. . С 1591 г. мы пользуемся формулами при решении квадратных уравнений Вспомни алгебраический способ решения квадратных
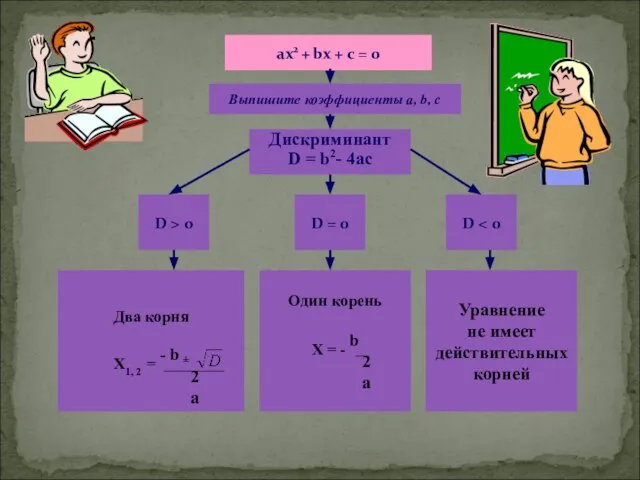
- 14. ах2 + bх + с = 0 Выпишите коэффициенты a, b, c Дискриминант D = b2-
- 15. Формулировка т. Виета. Обратная т. Виета. Зависимость знаков корней квадратного уравнения, от коэффициентов.
- 16. Если второй коэффициент уравнения чётный , можно использовать иную формулу – формулу чётных коэффициентов.
- 17. Квадратные уравнения можно решить, используя свойства «суммы коэффициентов» ах2 + bх + с =0 Если в
- 18. В учебнике мы встречаем задания , где четко обозначено , как решить квадратное уравнение . В
- 19. Задача №1 Известно, что учет населения проводился в Египте и в Китае ещё до нашей эры.
- 20. Задача №2 На основе статистических данных можно выделить регионы с максимальным сбросом загрязнённых вод: это Краснодарский
- 21. Кислотные осадки разрушают сооружения из мрамора и других материалов. Исторические памятники Греции и Рима , постояв
- 23. Подведение итогов Наш урок подходит к концу, подумайте о том с какой пользой для вас прошёл
- 24. « Теория без практики мертва и бесплодна, практика без теории невозможна и пагубна. Для теории нужны
- 26. Скачать презентацию




















 Итоговый урок физика8 класс
Итоговый урок физика8 класс Кто знает обо всём
Кто знает обо всём Дизайн как вид изобразительного искусства
Дизайн как вид изобразительного искусства Разработка домашнего задания на тему: матрешка
Разработка домашнего задания на тему: матрешка Аймактардын социалдык-экономикалык ?н?г?? тенденциясы
Аймактардын социалдык-экономикалык ?н?г?? тенденциясы Программа модернизации системы среднего профессионального образования Республики Карелия
Программа модернизации системы среднего профессионального образования Республики Карелия Ну-ка, проверь-ка, дружок, Ты готов начать урок? Всё ль на месте, всё ль в порядке, Ручка, книжка и тетрадка? Все ли правильно сидят? Вс
Ну-ка, проверь-ка, дружок, Ты готов начать урок? Всё ль на месте, всё ль в порядке, Ручка, книжка и тетрадка? Все ли правильно сидят? Вс HTML Первые шаги.
HTML Первые шаги. Формы сохранения культурного наследия
Формы сохранения культурного наследия Выбирай банк смолоду: предложение Райффайзенбанка для молодёжи от команды Giants
Выбирай банк смолоду: предложение Райффайзенбанка для молодёжи от команды Giants Месяц тотального рекрутинга. Только в апреле каждому новичку КЭШБЭК 10%
Месяц тотального рекрутинга. Только в апреле каждому новичку КЭШБЭК 10% Типичные задачи по математике
Типичные задачи по математике Анимация кроссвордовколлективное творчество участников сообщества "ИКТ в НШ"
Анимация кроссвордовколлективное творчество участников сообщества "ИКТ в НШ"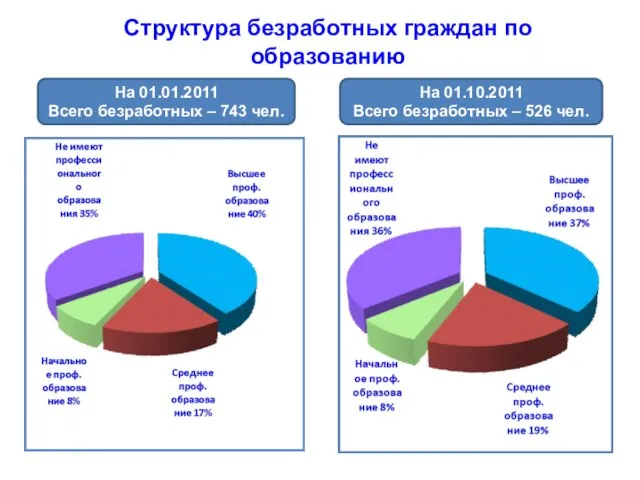 Структура безработных граждан по образованию
Структура безработных граждан по образованию Дистанционный Кадавер курс
Дистанционный Кадавер курс Оценка безопасности комбинации индометацина и тиотриазолина по влиянию на слизистую желудка
Оценка безопасности комбинации индометацина и тиотриазолина по влиянию на слизистую желудка Линии одним росчерком пера
Линии одним росчерком пера Political System of Kazakhstan
Political System of Kazakhstan  Семья Яковлевых прдставляет
Семья Яковлевых прдставляет История расчески
История расчески Какими средствами воздействует искусство? 7 класс
Какими средствами воздействует искусство? 7 класс Физика и искусство
Физика и искусство Как общаться с подростком
Как общаться с подростком Как посвятить учеников в ряды пятиклассников
Как посвятить учеников в ряды пятиклассников 20140928_dimova_v.m.priem_rabota_s_risunkami._tektonicheskaya_karta
20140928_dimova_v.m.priem_rabota_s_risunkami._tektonicheskaya_karta Роберт Шуман
Роберт Шуман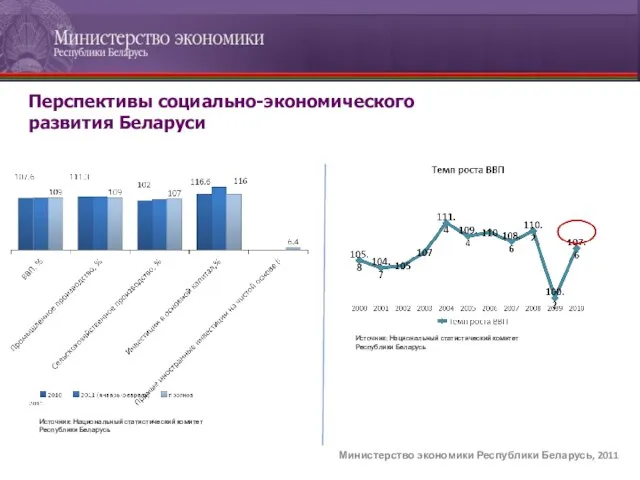 Перспективы социально-экономического развития Беларуси
Перспективы социально-экономического развития Беларуси Презентация на тему Правовой статус таможенного перевозчика
Презентация на тему Правовой статус таможенного перевозчика