Слайд 21. Определение ранга матрицы. Свойства ранга матрицы
Рангом матрицы называют наибольший из порядков

ее миноров, отличных от нуля (обозначается r(А) или rangA).
Свойства ранга матрицы:
1) если матрица A имеет размеры mхn, то rangA≤min(m;n);
2) rangA=0 тогда и только тогда, когда все элементы матрицы A равны нулю;
3) если матрица A – квадратная порядка n, то rangA =n тогда и только тогда, когда |A|≠0.
назад
Слайд 32. Способы нахождения ранга матрицы
Используя определение и свойства ранга матрицы
Используя свойство миноров
Используя

элементарные преобразования
назад
Слайд 4Данный способ (используя определение и свойства ранга матрицы) удобно применять при нахождения

ранга матрицы «небольшой» размерности.
Пример 1. Вычислить ранги следующих матриц
Решение
назад
Слайд 5Решение (Пример 1). Вычислить ранги следующих матриц
назад

Слайд 6Данный способ (используя свойство миноров) удобно применять при нахождения ранга матрицы с

«большим количеством» нулевых элементов.
Свойство миноров. Если все миноры порядка k данной матрицы равны нулю, то все миноры более высокого порядка также равны нулю.
Метод: Если среди миноров порядка k данной матрицы есть отличные от нуля, а все миноры порядка (k+1) равны нулю или не существуют, то ранг матрицы равен k.
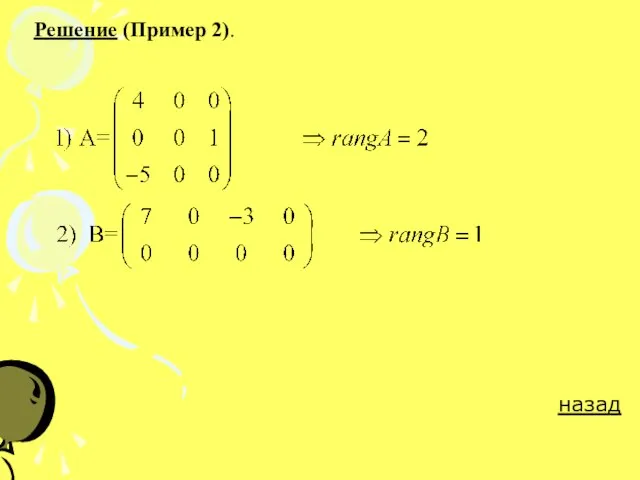
Пример 2. Вычислить ранги следующих матриц
РешениеРешение назад
Слайд 8Данный способ нахождения ранга матрицы (используя элементарные преобразования) удобно применять к матрице

любой размерности.
Метод: с помощью элементарных преобразований свести матрицу к ступенчатому виду или квазитреугольной форме
где ≠0, i=1,…,r; r≤k, тогда ранг матрицы равен r.
Пример 3.
назад
Слайд 9Элементарные преобразования,
не меняющие ранга матрицы:
отбрасывание нулевой строки (столбца);
умножение всех элементов строки

(столбца) матрицы на число, не равное нулю;
изменение порядка строк (столбцов) матрицы;
прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;
транспонирование матрицы.
назад
Слайд 10Пример 3. Найти ранг матрицы
С помощью элементарных преобразований приведем матрицу к ступенчатому

виду:
далее
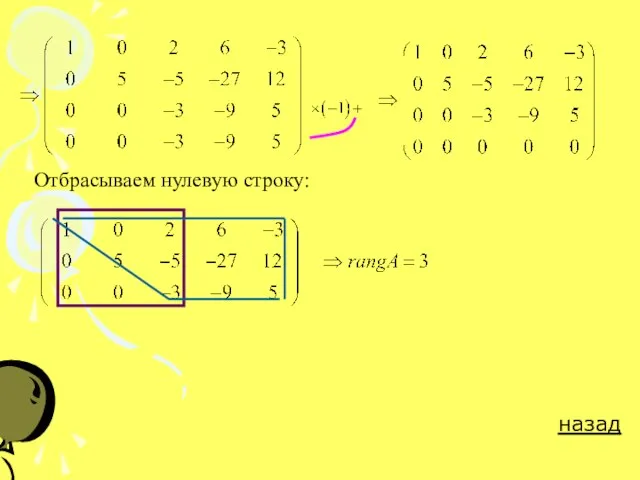
Слайд 11
Отбрасываем нулевую строку:
назад
Слайд 123. Теорема о ранге матрицы
Строки (столбцы) матрицы , называются линейно зависимыми, если

существуют такие числа , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
. В противном случае строки матрицы называются линейно независимыми.
Теорема о ранге матрицы: ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов.
Пример 4.
назад
Слайд 13Пример 4. Найти максимальное число линейно независимых строк матрицы
С помощью элементарных преобразований

приведем матрицу к ступенчатому виду:
далее
Слайд 14
Отбрасываем нулевые строки:
Следовательно, по теореме о ранге матрицы исходная матрица имеет две
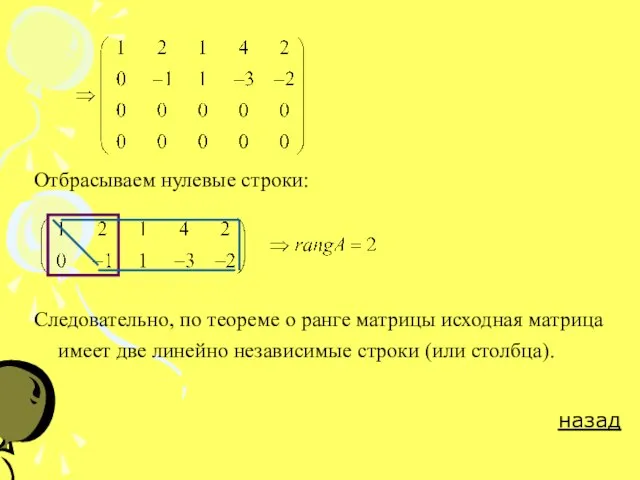
линейно независимые строки (или столбца).
назад












 Политическая сфера общества
Политическая сфера общества Мерчандайзинг
Мерчандайзинг Деревья нашего города
Деревья нашего города ДЕНЬ МАТЕРИ
ДЕНЬ МАТЕРИ Презентация на тему Работа с пластилином 1 класс
Презентация на тему Работа с пластилином 1 класс Презентация на тему Общие рекомендации по поведению при опасных явлениях природы
Презентация на тему Общие рекомендации по поведению при опасных явлениях природы Слагаемые успеха в бизнесе
Слагаемые успеха в бизнесе Экологически безопасный дом
Экологически безопасный дом Презентация на тему Формы земной поверхности
Презентация на тему Формы земной поверхности Своя
Своя Виріб в техніці кінусайга
Виріб в техніці кінусайга Презентация на тему Растительный организм
Презентация на тему Растительный организм Немецкая классическая философия
Немецкая классическая философия Пистолет-пулемет Судаева
Пистолет-пулемет Судаева Первый закон Ньютона
Первый закон Ньютона Тундра и Арктическая пустыня.
Тундра и Арктическая пустыня. Типы и структура уроков по ФГОС
Типы и структура уроков по ФГОС Иван Федорович Крузенштерн (1770-1846 гг.)
Иван Федорович Крузенштерн (1770-1846 гг.) Пищевые добавки (1 класс)
Пищевые добавки (1 класс) Prezentatsia
Prezentatsia Томскнипинефть
Томскнипинефть Инструменты маркетинга.Ценообразование
Инструменты маркетинга.Ценообразование Коллективная работа
Коллективная работа Федор Михайлович Достоевский. Портрет писателя
Федор Михайлович Достоевский. Портрет писателя Балясины
Балясины Тренинг продаж
Тренинг продаж Вебинар «Секреты привлечения абитуриентов и эффективная работа приемной комиссии с помощью программного продукта «1С:Колледж»
Вебинар «Секреты привлечения абитуриентов и эффективная работа приемной комиссии с помощью программного продукта «1С:Колледж» Презентация на тему Переработка нефти
Презентация на тему Переработка нефти