Содержание
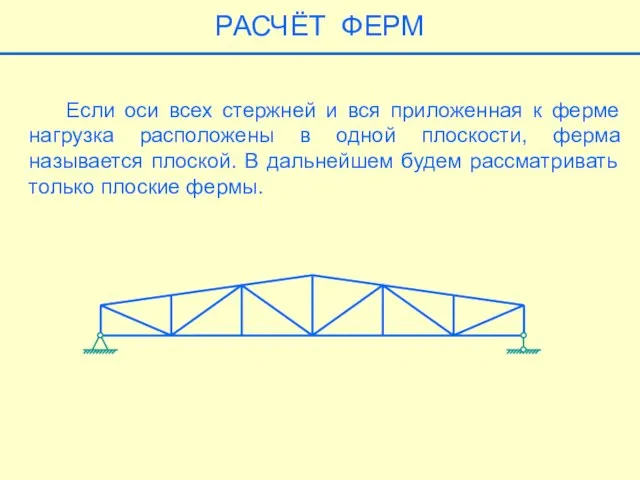
- 12. Если оси всех стержней и вся приложенная к ферме нагрузка расположены в одной плоскости, ферма называется
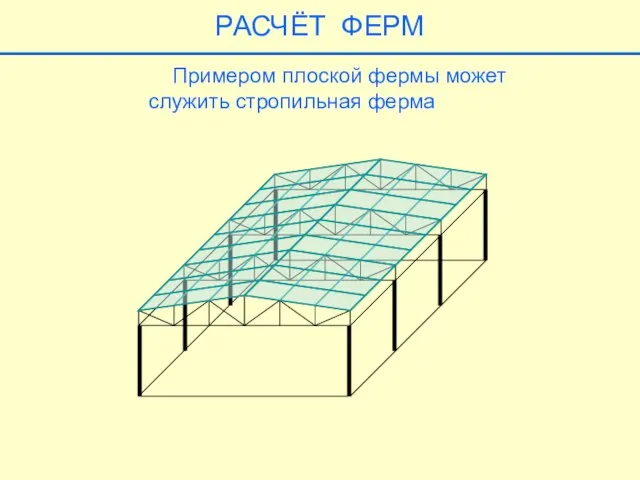
- 13. РАСЧЁТ ФЕРМ Примером плоской фермы может служить стропильная ферма
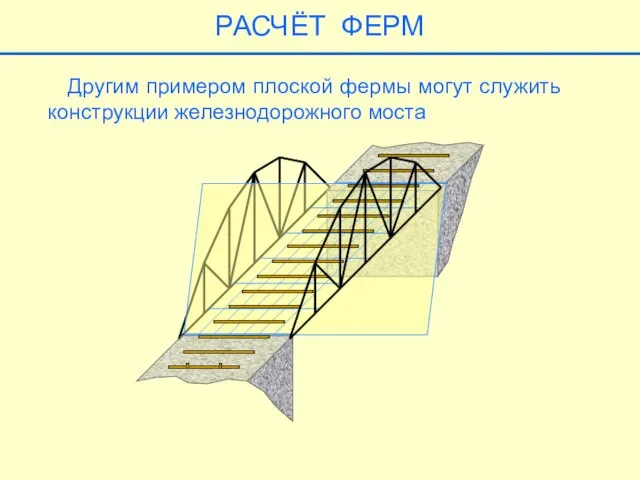
- 15. РАСЧЁТ ФЕРМ Другим примером плоской фермы могут служить конструкции железнодорожного моста
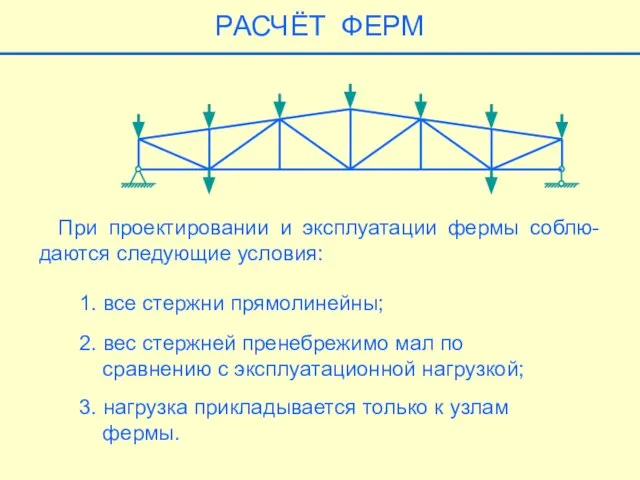
- 16. При проектировании и эксплуатации фермы соблю-даются следующие условия: 1. все стержни прямолинейны; 2. вес стержней пренебрежимо
- 17. РАСЧЁТ ФЕРМ Как видно, нагрузка на ферму передаётся через продольные прогоны, которые прикреплены к узлам фермы.
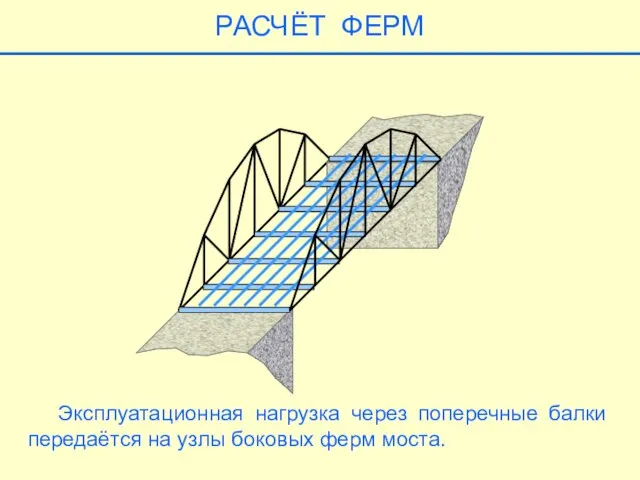
- 18. РАСЧЁТ ФЕРМ Эксплуатационная нагрузка через поперечные балки передаётся на узлы боковых ферм моста.
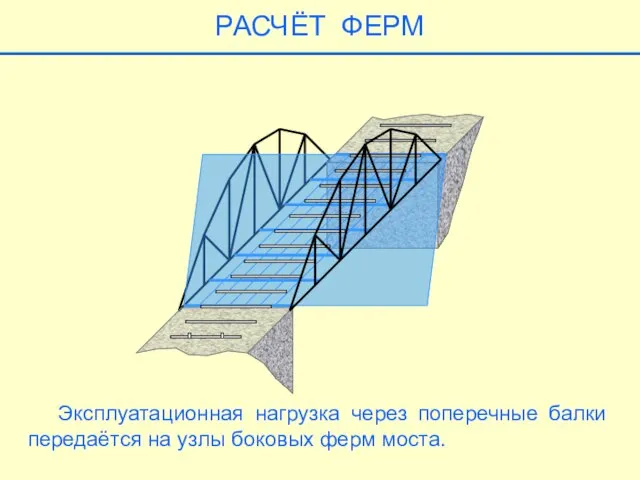
- 19. РАСЧЁТ ФЕРМ Эксплуатационная нагрузка через поперечные балки передаётся на узлы боковых ферм моста.
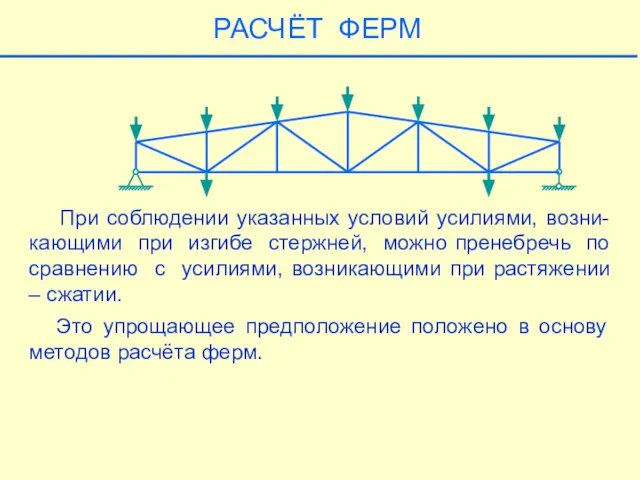
- 20. При соблюдении указанных условий усилиями, возни-кающими при изгибе стержней, можно пренебречь по сравнению с усилиями, возникающими
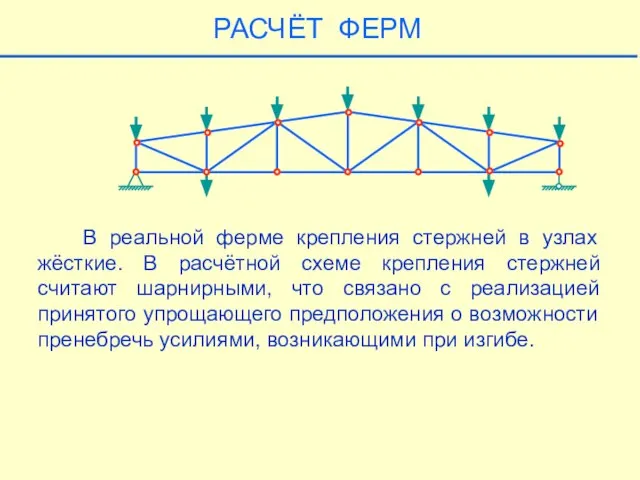
- 21. РАСЧЁТ ФЕРМ В реальной ферме крепления стержней в узлах жёсткие. В расчётной схеме крепления стержней считают
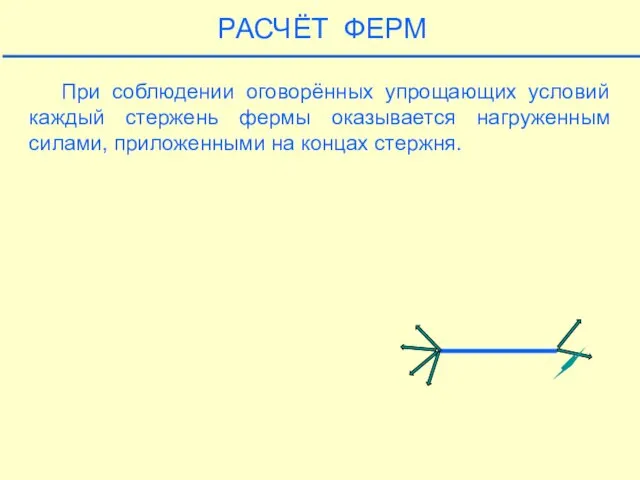
- 22. РАСЧЁТ ФЕРМ При соблюдении оговорённых упрощающих условий каждый стержень фермы оказывается нагруженным силами, приложенными на концах
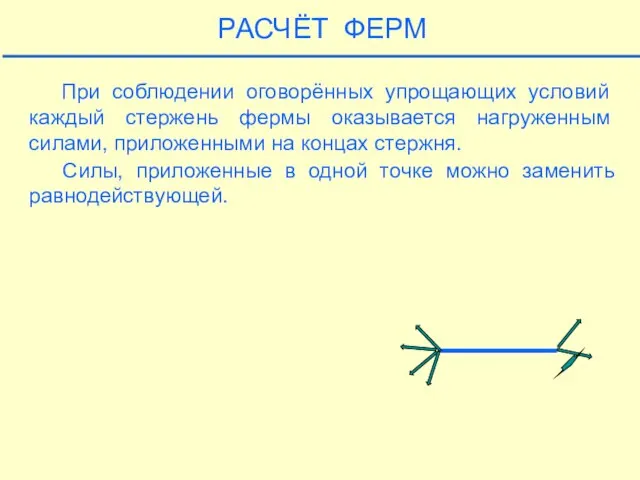
- 23. РАСЧЁТ ФЕРМ При соблюдении оговорённых упрощающих условий каждый стержень фермы оказывается нагруженным силами, приложенными на концах
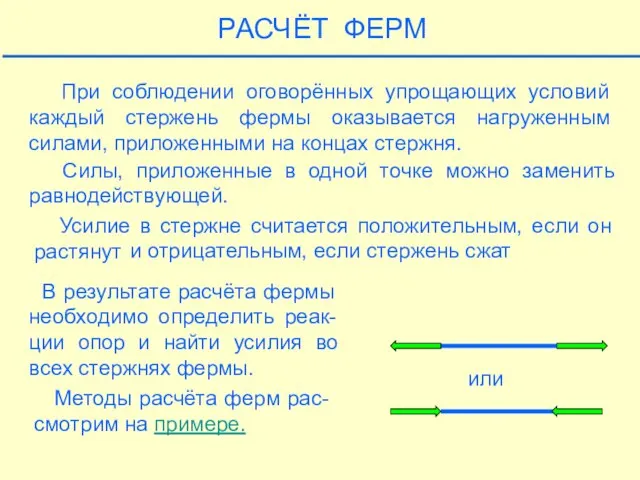
- 24. или РАСЧЁТ ФЕРМ При соблюдении оговорённых упрощающих условий каждый стержень фермы оказывается нагруженным силами, приложенными на
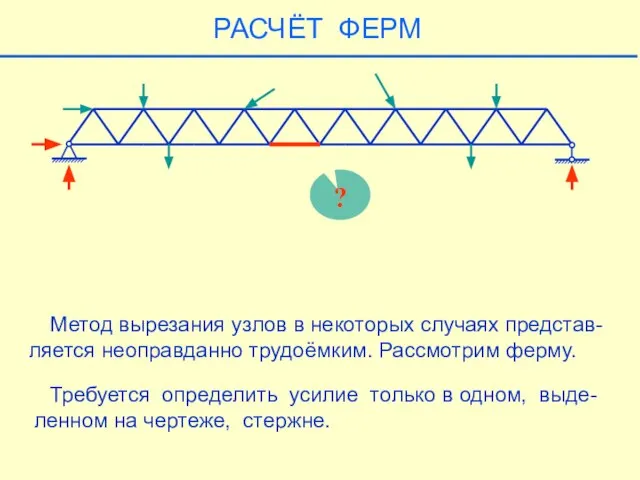
- 25. ? Метод вырезания узлов в некоторых случаях представ- ляется неоправданно трудоёмким. Рассмотрим ферму. Требуется определить усилие
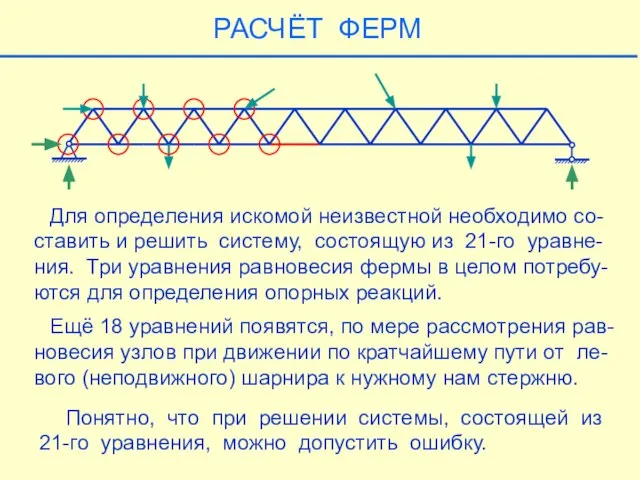
- 26. Для определения искомой неизвестной необходимо со-ставить и решить систему, состоящую из 21-го уравне-ния. Три уравнения равновесия
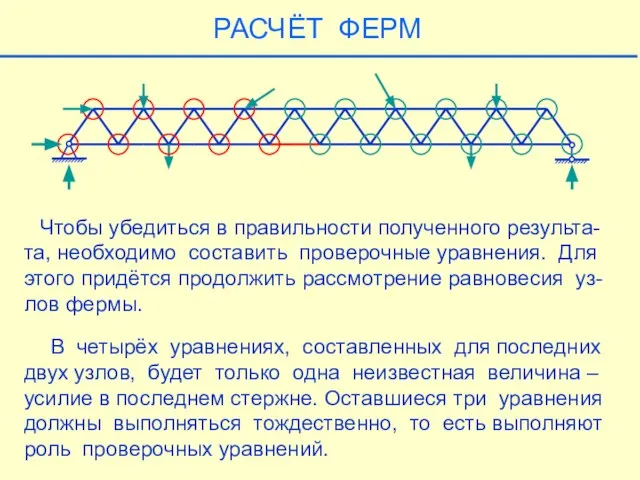
- 27. Чтобы убедиться в правильности полученного результа-та, необходимо составить проверочные уравнения. Для этого придётся продолжить рассмотрение равновесия
- 28. Понятно, что результат проверки может быть разным. Возможны варианты. Первый вариант Второй вариант РАСЧЁТ ФЕРМ
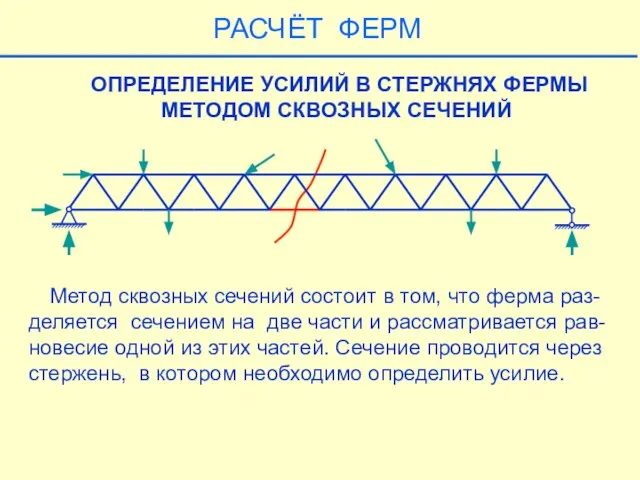
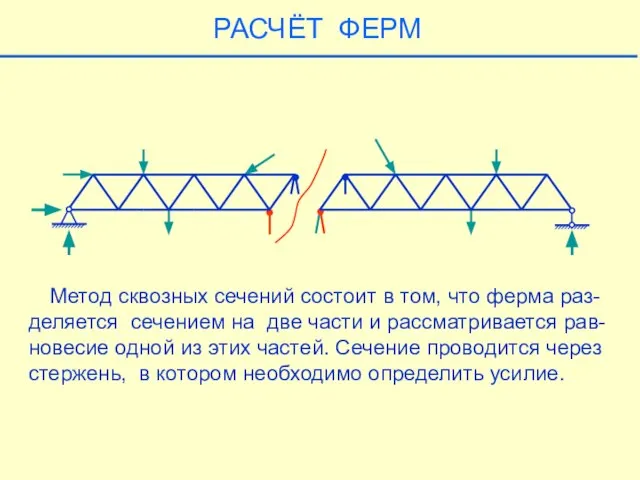
- 29. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ ФЕРМЫ МЕТОДОМ СКВОЗНЫХ СЕЧЕНИЙ Метод сквозных сечений состоит в том, что ферма
- 30. Метод сквозных сечений состоит в том, что ферма раз- деляется сечением на две части и рассматривается
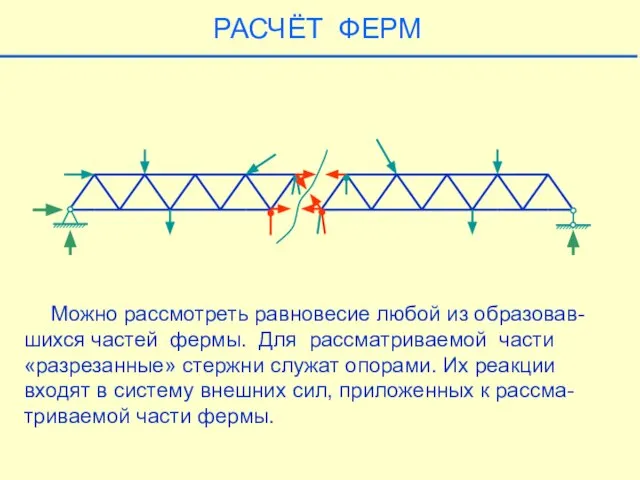
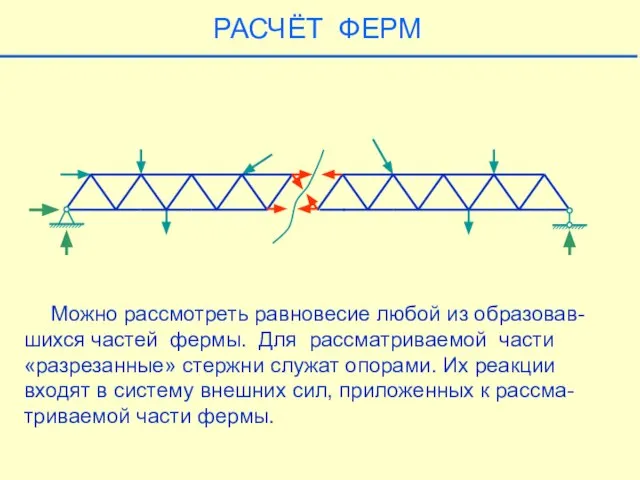
- 31. Можно рассмотреть равновесие любой из образовав-шихся частей фермы. Для рассматриваемой части «разрезанные» стержни служат опорами. Их
- 32. РАСЧЁТ ФЕРМ Можно рассмотреть равновесие любой из образовав-шихся частей фермы. Для рассматриваемой части «разрезанные» стержни служат
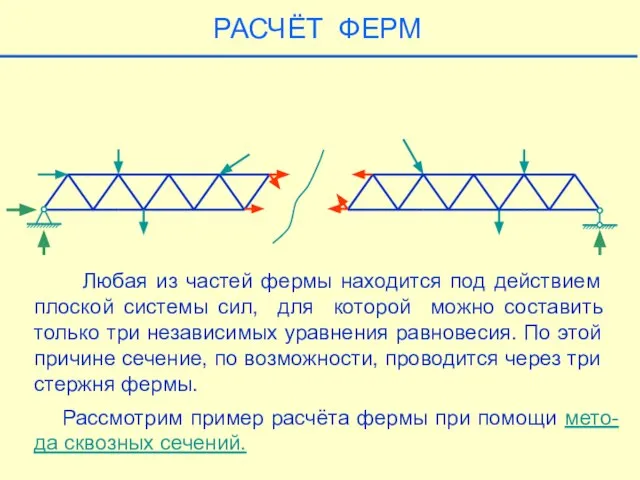
- 33. РАСЧЁТ ФЕРМ Любая из частей фермы находится под действием плоской системы сил, для которой можно составить
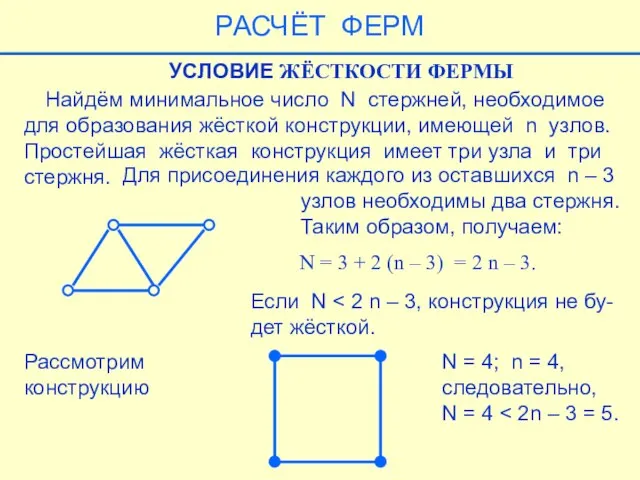
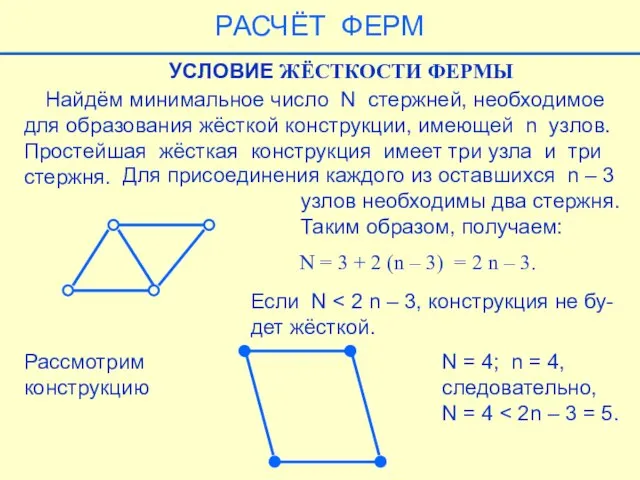
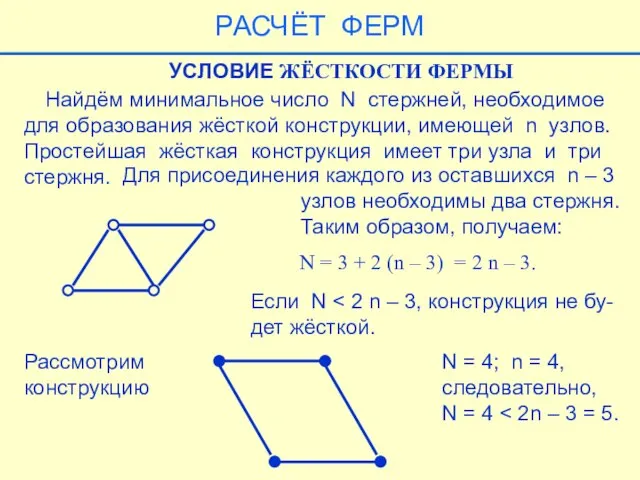
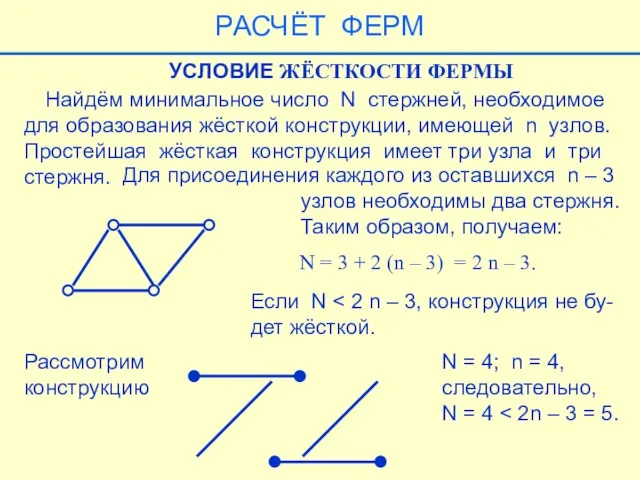
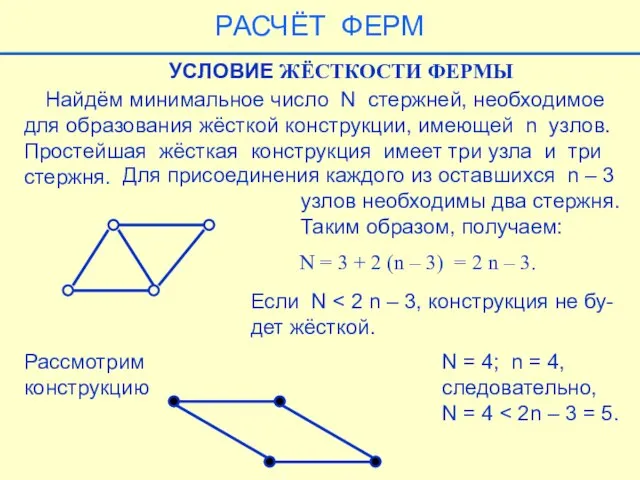
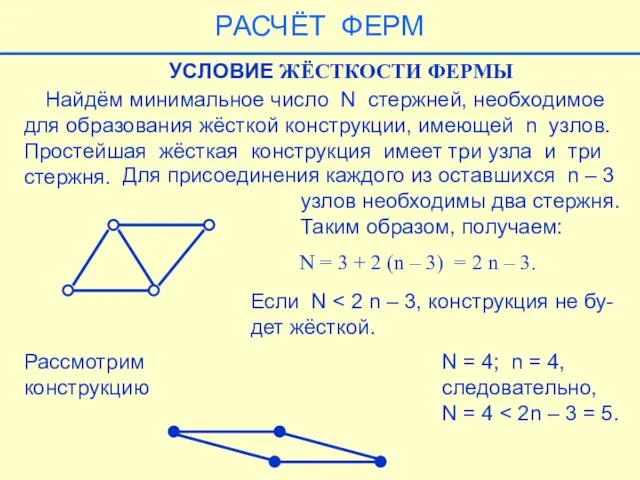
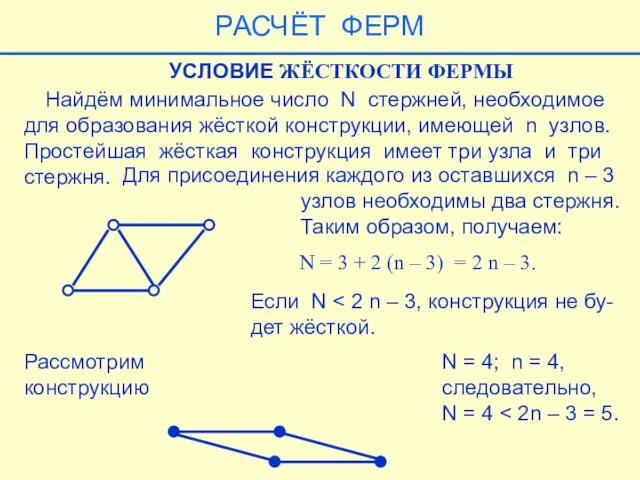
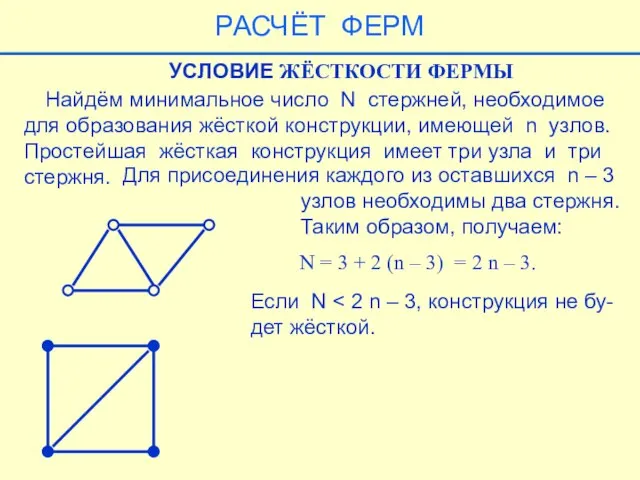
- 34. Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция
- 35. Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция
- 36. Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция
- 37. Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция
- 38. Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция
- 39. Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция
- 40. Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция
- 41. Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция
- 42. Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция
- 43. Найдём минимальное число N стержней, необходимое для образования жёсткой конструкции, имеющей n узлов. Простейшая жёсткая конструкция
- 44. УСЛОВИЕ СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ ФЕРМЫ Ферма называется статически определимой, если чис- ло неизвестных равно числу уравнений равновесия,
- 46. Скачать презентацию















 Смысл названия романа «Тихий Дон»
Смысл названия романа «Тихий Дон» Innocence & amitié
Innocence & amitié Этапы проведения кабинетных маркетинговых исследований
Этапы проведения кабинетных маркетинговых исследований Московский Кремль (2 класс)
Московский Кремль (2 класс) ТРАДИЦИОННЫЙ И АЛЬТЕРНАТИВНЫЙ МЕНЕДЖМЕНТ ЧЕРЕЗ ПРИЗМУ АГЕНТСКОЙ МОДЕЛИ
ТРАДИЦИОННЫЙ И АЛЬТЕРНАТИВНЫЙ МЕНЕДЖМЕНТ ЧЕРЕЗ ПРИЗМУ АГЕНТСКОЙ МОДЕЛИ Что такое NAUKA 0+
Что такое NAUKA 0+ Презентация на тему Графика в Паскаль
Презентация на тему Графика в Паскаль  День матери России
День матери России Good-looking
Good-looking  Текст Мы идем в зоопарк
Текст Мы идем в зоопарк Николай Иванович Кареев (1850-1931)– теоретик и методолог
Николай Иванович Кареев (1850-1931)– теоретик и методолог Структура ВС РФ. Виды ВС РФ. Тест
Структура ВС РФ. Виды ВС РФ. Тест Великая Отечественная война в Заполярье
Великая Отечественная война в Заполярье Церковь Иль-Джезу
Церковь Иль-Джезу в Стрежевом 5 лет
в Стрежевом 5 лет Презентация на тему число и цифра 2
Презентация на тему число и цифра 2  моу Ромненская сош Проект «Улицы моего села»
моу Ромненская сош Проект «Улицы моего села» Путешествие на планету положительных и отрицательных чисел
Путешествие на планету положительных и отрицательных чисел Милли ризыклар
Милли ризыклар СХЕМА РАЗМЕЩЕНИЯ НЕСТАЦИОНАРНЫХ ТОРГОВЫХ ОБЪЕКТОВ НА ТЕРРИТОРИИ ГНИЛОВСКОГО СЕЛЬСКОГО ПОСЕЛЕНИЯ ОСТРОГОЖСКОГО МУНИЦИПАЛЬНОГО Р
СХЕМА РАЗМЕЩЕНИЯ НЕСТАЦИОНАРНЫХ ТОРГОВЫХ ОБЪЕКТОВ НА ТЕРРИТОРИИ ГНИЛОВСКОГО СЕЛЬСКОГО ПОСЕЛЕНИЯ ОСТРОГОЖСКОГО МУНИЦИПАЛЬНОГО Р Способы выражения будущего времени
Способы выражения будущего времени Предмет Мировая художественная культура
Предмет Мировая художественная культура Криминалистическое оружиеведение. Тема 6
Криминалистическое оружиеведение. Тема 6 Современная наука
Современная наука Природные комплексы суши и океана
Природные комплексы суши и океана Генераторы ГЭС
Генераторы ГЭС Презентация на тему Крещенские святки
Презентация на тему Крещенские святки  Роль Уполномоченного в формировании региональной политики в защиту прав детей
Роль Уполномоченного в формировании региональной политики в защиту прав детей