Содержание
- 2. 1. Резьбовые соединения. Общие сведения Объекты расчета — групповые резьбовые соединения, выполненные с помощью стандартных крепежных
- 3. 1. Резьбовые соединения. Общие сведения Стальные крепежные детали (болты, винты и шпильки) в соответствии с ГОСТ
- 4. 2.1. Групповое резьбовое соединение, нагруженное в плоскости стыка силами и моментами Пример соединения приведен на рисунке
- 5. 2.1. Групповое резьбовое соединение, нагруженное в плоскости стыка силами и моментами Болты установлены без зазора (см.
- 6. 2.1. Групповое резьбовое соединение, нагруженное в плоскости стыка силами и моментами 3). определяют из расчета болта
- 7. 2.1. Групповое резьбовое соединение, нагруженное в плоскости стыка силами и моментами Значения коэффициентов трения приведены в
- 8. 2.1. Групповое резьбовое соединение, нагруженное в плоскости стыка силами и моментами Силы трения в стыке с
- 9. 2.2. Групповое резьбовое соединение, нагруженное в плоскости, перпендикулярной стыку Пример соединения приведен на рис. 3.6, где
- 10. 2.2. Групповое резьбовое соединение, нагруженное в плоскости, перпендикулярной стыку Внешние нагрузки (F, M) распределяются между резьбовыми
- 11. 2.2. Групповое резьбовое соединение, нагруженное в плоскости, перпендикулярной стыку Вперед © В.Б. Тарабарин «Семинары по курсу
- 12. 2.2. Групповое резьбовое соединение, нагруженное в плоскости, перпендикулярной стыку Вперед © В.Б. Тарабарин «Семинары по курсу
- 13. 2.3. Групповое резьбовое соединение, нагруженное в плоскости стыка и в плоскости, перпендикулярной стыку Вперед © В.Б.
- 14. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ В варианте a (см. рис. 3.8)
- 15. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.5. Допускаемые напряжения при статической нагрузке
- 16. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.6. Пример расчета группового резьбового соединения,
- 17. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.6. Пример расчета группового резьбового соединения,
- 18. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.6. Пример расчета группового резьбового соединения,
- 19. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.6. Пример расчета группового резьбового соединения,
- 20. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.6. Пример расчета группового резьбового соединения,
- 21. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.6. Пример расчета группового резьбового соединения,
- 22. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.6. Пример расчета группового резьбового соединения,
- 23. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.7. Пример расчета группового резьбового соединения,
- 24. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.7. Пример расчета группового резьбового соединения,
- 25. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.7. Пример расчета группового резьбового соединения,
- 26. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.7. Пример расчета группового резьбового соединения,
- 27. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.7. Пример расчета группового резьбового соединения,
- 28. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.7. Пример расчета группового резьбового соединения,
- 29. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.7. Пример расчета группового резьбового соединения,
- 30. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ Напряжение среза в резьбе болта (винта)
- 31. Вперед © В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ 2.8. Проверка прочности элементов резьбы
- 33. Скачать презентацию
Слайд 21. Резьбовые соединения. Общие сведения
Объекты расчета — групповые резьбовые соединения, выполненные
1. Резьбовые соединения. Общие сведения
Объекты расчета — групповые резьбовые соединения, выполненные
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
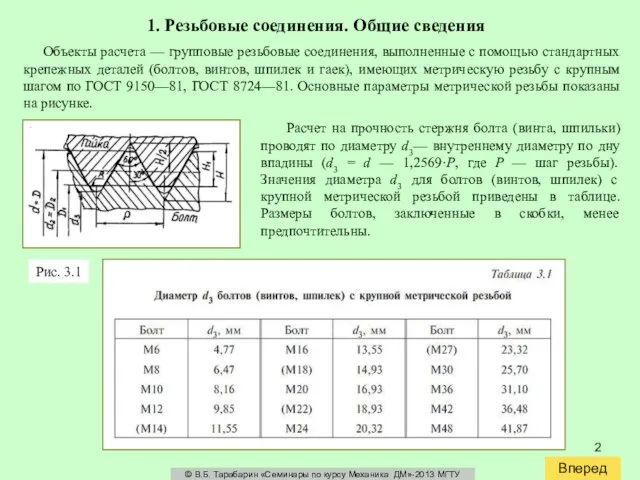
Расчет на прочность стержня болта (винта, шпильки) проводят по диаметру d3— внутреннему диаметру по дну впадины (d3 = d — 1,2569·P, где Р — шаг резьбы). Значения диаметра d3 для болтов (винтов, шпилек) с крупной метрической резьбой приведены в таблице. Размеры болтов, заключенные в скобки, менее предпочтительны.
Рис. 3.1
Слайд 31. Резьбовые соединения. Общие сведения
Стальные крепежные детали (болты, винты и шпильки)
1. Резьбовые соединения. Общие сведения
Стальные крепежные детали (болты, винты и шпильки)
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
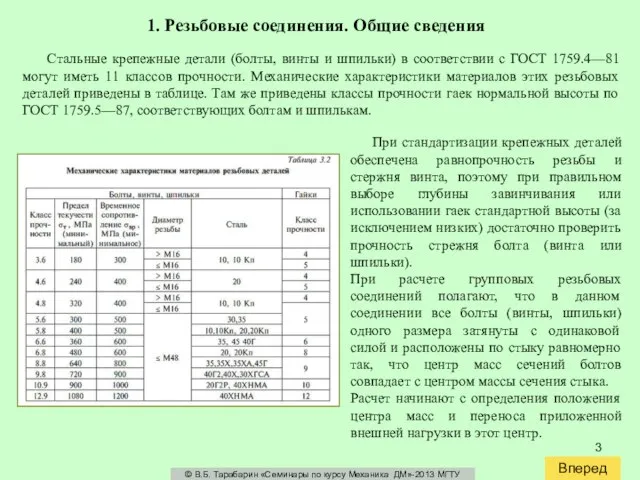
При стандартизации крепежных деталей обеспечена равнопрочность резьбы и стержня винта, поэтому при правильном выборе глубины завинчивания или использовании гаек стандартной высоты (за исключением низких) достаточно проверить прочность стрежня болта (винта или шпильки).
При расчете групповых резьбовых соединений полагают, что в данном соединении все болты (винты, шпильки) одного размера затянуты с одинаковой силой и расположены по стыку равномерно так, что центр масс сечений болтов совпадает с центром массы сечения стыка.
Расчет начинают с определения положения центра масс и переноса приложенной внешней нагрузки в этот центр.
Слайд 42.1. Групповое резьбовое соединение, нагруженное в плоскости стыка силами и моментами
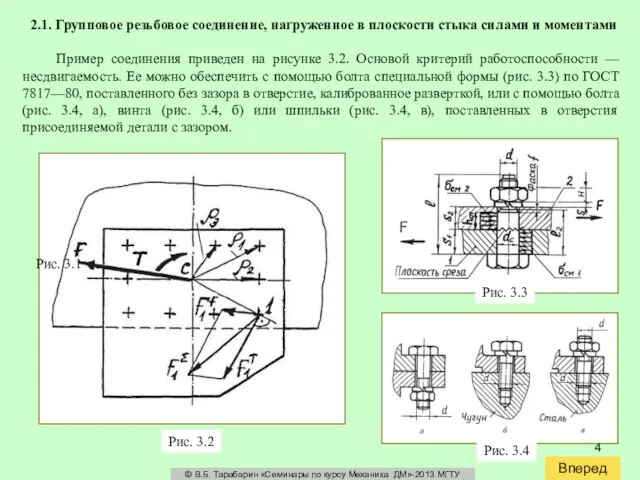
Пример
2.1. Групповое резьбовое соединение, нагруженное в плоскости стыка силами и моментами
Пример
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
Рис. 3.1
Рис. 3.2
Рис. 3.3
Рис. 3.4
Слайд 52.1. Групповое резьбовое соединение, нагруженное в плоскости стыка силами и моментами
Болты
2.1. Групповое резьбовое соединение, нагруженное в плоскости стыка силами и моментами
Болты

Несдвигаемость деталей соединения относительно друг друга обеспечивается за счет сопротивления: а) срезу стержня болта, б) смятию боковой поверхности болта и соединяемых деталей.
Расчет ведут, полагая, что силы Fi , приходящиеся на болты от действия центральных внешних сил (см. рис. 3.2), равны, т. е.
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
где z — число болтов.
Силы, нагружающие болты из-за действия момента T, пропорциональны расстояниям ρi- от болтов до центра масс. Максимально нагружены наиболее удаленные, на которые действует сила
где ρmax — расстояние от центра масс до наиболее удаленного болта.
Расчет ведут в такой последовательности:
1). определяют силы, приходящиеся на болты от действия отдельных силовых факторов;
2). находят для наиболее нагруженного болта путем геометрического сложения суммарную действующую на него силу FΣ1max (см. рис. 3.2);
Слайд 62.1. Групповое резьбовое соединение, нагруженное в плоскости стыка силами и моментами
3).
2.1. Групповое резьбовое соединение, нагруженное в плоскости стыка силами и моментами
3).

4). округляют полученное значение диаметра стержня dc до стандартного (ГОСТ 7817—80);
5). рассчитывают длину болта: а) полную, l; б) нарезанной части, (l — 12); в) минимальную, сопротивляющуюся смятию, hсм;
6). проверяют правильность принятых размеров расчетом на смятие.
Напряжения смятия σсм условно считают равномерно распределенными по площади, являющейся проекцией поверхности смятия на плоскость, перпендикулярную действующей силе.
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
Болты (винты, шпильки) установлены с зазором (см. рис. 3.4). Если от расчета не требуется повышенная точность, то приближенно полагают, что нагрузка в стыке локализуется в непосредственной близости от отверстий под болты (исключения оговорены ниже). Силу FΣ1max , действующую на наиболее нагруженный болт, определяют, как и для болта, поставленного без зазора.
Условие отсутствия сдвига (несдвигаемости) имеет вид
где F1тр — сила трения, созданная при затяжке одного болта (винта, шпильки), kсц — коэффициент запаса сцепления (запаса по несдвигаемости), принимают kсц > 1,5.
В свою очередь,
где Fзат — сила затяжки одного болта, f — коэффициент трения на стыке, i — число рабочих стыков.
Слайд 72.1. Групповое резьбовое соединение, нагруженное в плоскости стыка силами и моментами
Значения
2.1. Групповое резьбовое соединение, нагруженное в плоскости стыка силами и моментами
Значения

Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
При нагружении соединения только центральной сдвигающей силой F условие отсутствия сдвига может быть записано в более простой форме:
где Fтр — суммарная сила трения на стыке деталей.
При нагружении соединения только сдвигающим моментом Т условие отсутствия сдвига имеет вид
где Ттр — суммарный момент сил трения на стыке деталей.
Слайд 82.1. Групповое резьбовое соединение, нагруженное в плоскости стыка силами и моментами
Силы
2.1. Групповое резьбовое соединение, нагруженное в плоскости стыка силами и моментами
Силы

Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
Расчетные зависимости для стыков иных форм приведены в работах [1 — 4].
Из условий (3.1) — (3.4) находят необходимую силу затяжки Fзат каждого из болтов.
где [σ]р — допускаемое напряжение растяжения стержня болта (cм.
табл. 3.4).
На болт (винт, шпильку) внешняя сдвигающая нагрузка не передается. Необходимую площадь Aр поперечного сечения болта по диаметру d3 и необходимый диаметр d3 (а по нему и номинальный диаметр резьбы d) при проектном расчете определяют из условия прочности стержня болта при затяжке с силой Fзат:
При затягивании в стержне болта за счет трения в резьбе возникают касательные напряжения кручения, что учитывают, вводя коэффициент перед силой. Для стандартных крепежных деталей при средних условиях трения в резьбе этот коэффициент равен 1,3.
Рис. 3.5
Слайд 92.2. Групповое резьбовое соединение, нагруженное в плоскости, перпендикулярной стыку
Пример соединения приведен
2.2. Групповое резьбовое соединение, нагруженное в плоскости, перпендикулярной стыку
Пример соединения приведен

В общем случае нужно обеспечить: 1) нераскрытие стыка, 2) прочность болтов, 3) прочность основания (для неметаллического основания).
В общей форме условие нераскрытия стыка может быть записано так:
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
где σmin ст — минимальное напряжение сжатия в стыке после приложения внешней нагрузки.
Для выполнения условия (3.6) вводят коэффициент запаса по нераскрытию стыка k = 1,3...1,5 (k = 1,1 — для малоответственных соединений).
Из условия (3.6) определяют необходимую для предотвращения раскрытия стыка силу Fзат каждого болта (винта, шпильки).
Рис. 3.6
Слайд 102.2. Групповое резьбовое соединение, нагруженное в плоскости, перпендикулярной стыку
Внешние нагрузки (F,
2.2. Групповое резьбовое соединение, нагруженное в плоскости, перпендикулярной стыку
Внешние нагрузки (F,

Условие нераскрытия стыка, выраженное через напряжения на стыке, принимает вид
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
Напряжение сжатия на стыке от затяжки болтов (винтов или шпилек)
где z — число болтов на стыке; Аст — номинальная площадь стыка (без учета наличия отверстий под болты).
Напряжение на стыке от действия внешней нормальной к стыку силы
Знаки «+» или «—» перед σFN в формулах: верхний — при раскрывающей стык нагрузке, нижний — в том случае, когда нагрузка увеличивает напряжения сжатия на стыке
Слайд 112.2. Групповое резьбовое соединение, нагруженное в плоскости, перпендикулярной стыку
Вперед
© В.Б. Тарабарин «Семинары
2.2. Групповое резьбовое соединение, нагруженное в плоскости, перпендикулярной стыку
Вперед
© В.Б. Тарабарин «Семинары

Максимальное напряжение на стыке от опрокидывающего момента
После введения коэффициента запаса по нераскрытию к и преобразований условие нераскрытия стыка принимает вид
откуда видно, что при одинаковом для стыков разных форм значении ymax ст наиболее рациональным будет тот стык, у которого имеет максимальное значение отношение Ix ст /Аст. При этом будет минимальным значение необходимой силы по условию нераскрытия стыка.
Если нейтральная ось обозначена х— x, то
где — момент сопротивления стыка относительно нейтральной оси.
где Ix ст — момент инерции стыка относительно нейтральной оси;
ymax ст — расстояние от нейтральной оси до наиболее удаленных точек стыка с разгружаемой стороны стыка.
Необходимую площадь поперечного сечения болта Ар (проектный расчет) находят из условия прочности болта
где коэффициент 1,3 учитывает скручивание болта при его затяжке; FΣвн — суммарная внешняя растягивающая нагрузка, приходящаяся на наиболее нагруженный болт; Ар — площадь болта по диаметру d3.
Слайд 122.2. Групповое резьбовое соединение, нагруженное в плоскости, перпендикулярной стыку
Вперед
© В.Б. Тарабарин «Семинары
2.2. Групповое резьбовое соединение, нагруженное в плоскости, перпендикулярной стыку
Вперед
© В.Б. Тарабарин «Семинары

[σ]р — допускаемое напряжение растяжения для болта.
В свою очередь,
Пренебрегая моментом сопротивления болта относительно собственной центральной оси, можно записать
Чем больше Wx всех болтов, тем меньше напряжения, возникающие в болте. Поэтому оптимальным будет такое расположение болтов, при котором будет наибольшим значение отношения Σ (yi б)2/ ymах б .
где Wx всех болтов — момент сопротивления всех болтов относительно нейтральной оси x.
где σmах ст — максимальное напряжение сжатия на стыке после приложения внешней нагрузки (см. рис. 3.6); [σ]см — допускаемое напряжение смятия (табл. 3.5).
где y2i б — расстояние от нейтральной оси до некоторого i-го болта; ymах б — то же, для наиболее удаленного болта, находящегося на раскрываемой стороне стыка.
Неметаллическое основание проверяют по условию прочности на смятие
Слайд 132.3. Групповое резьбовое соединение, нагруженное в плоскости стыка и в плоскости, перпендикулярной
2.3. Групповое резьбовое соединение, нагруженное в плоскости стыка и в плоскости, перпендикулярной

Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
Необходимо обеспечить: 1) нераскрытие стыка (см. (3.6)); 2) несдвигаемость (см. (3.1)); 3) прочность болтов (см. (3.9)); 4) прочность основания (см. (3.10)), если оно неметаллическое.
Расчет болтов на прочность ведут по большей из двух сил затяжки, найденных из условия нераскрытия и несдвигаемости.
Стойку 1 (рис. 3.7) настольного сверлильного станка с помощью фланца 2 крепят шестью болтами 3 к основанию 4. На сверло действует сила резания Fрез. Определить оптимальный вариант расположения болтов на радиусе R стыка.
Решение. Сила резания Fрез создает опрокидывающий момент M = Fрез • L. Оптимально такое расположение болтов, при котором будет наибольшим отношение
2.4. Пример выбора оптимального варианта расположения болтов на кольцевом стыке
При равномерном расположении болтов по стыку рассмотрим два возможных варианта их постановки (рис. 3.8).
Рис. 3.7
Слайд 14Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
В варианте
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
В варианте

2.4. Пример выбора оптимального варианта расположения болтов на кольцевом стыке
Вывод: оптимальным является вариант б (см. рис. 3.8).
В варианте б четыре болта удалены от нейтральной оси на максимальное расстояние у1б = ymax б = R • sin 60° = 0,867 • R, а два других на у2б = 0. Следовательно,
Рис. 3.8
2.5. Допускаемые напряжения при статической нагрузке
Допускаемые напряжения для расчета болтов на растяжение
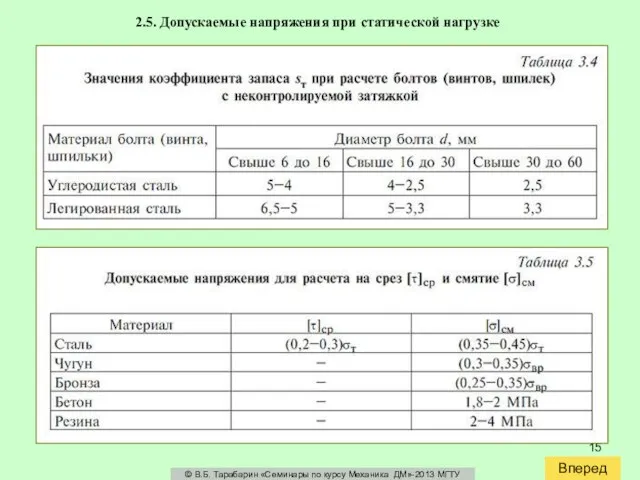
где σт — предел текучести материала болта (см. табл. 3.2); sт — коэффициент запаса прочности. Для ответственных резьбовых соединений силу затяжки контролируют. В этом случае sт = 1,2...1,5. Значения sт при неконтролируемой затяжке приведены в табл. 3.4
Слайд 15Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.5. Допускаемые напряжения
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.5. Допускаемые напряжения
Слайд 16Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.6. Пример расчета
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.6. Пример расчета

Блок 1 натяжного устройства (рис. 3.9) нагружен силой FQ = 12000 Н, созданной массой груза, и силой натяжения горизонтального каната FK = 12000 Н. Опоры оси блока размещены в корпусах 2. Каждый из корпусов прикреплен двумя болтами 3 к кронштейнам 4. Кронштейны крепятся к колонне 6 болтами 5. Число болтов крепления каждого кронштейна z = 6. Класс прочности болтов 5.8, они поставлены с зазором. Кронштейны 4 и колонна 6 изготовлены из горячекатаной стали Ст.3.
Размеры деталей: dб = 200 мм; l1 = 400 мм; l2 = 200 мм; a =80 мм; b = 80 мм; s1 = s2 = 10 мм.
Требуется определить диаметр болтов 5.
Решение.
1. Положение центра масс болтов 5. Центр масс болтов 5 находится в точке C, на пересечении осей симметрии соединения.
2. Перенос нагрузки в центр масс — точку C. Нагрузка от блока распределяется между двумя кронштейнами 4. Можно рассмотреть соединение одного кронштейна с колонной, нагруженное половиной внешней нагрузки. При переносе сил FQ/2 и FK/2 в точку C (рис. 3.10) получаем следующие силовые факторы:
вертикальную сдвигающую силу
Рис. 3.9
Слайд 17Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.6. Пример расчета
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.6. Пример расчета
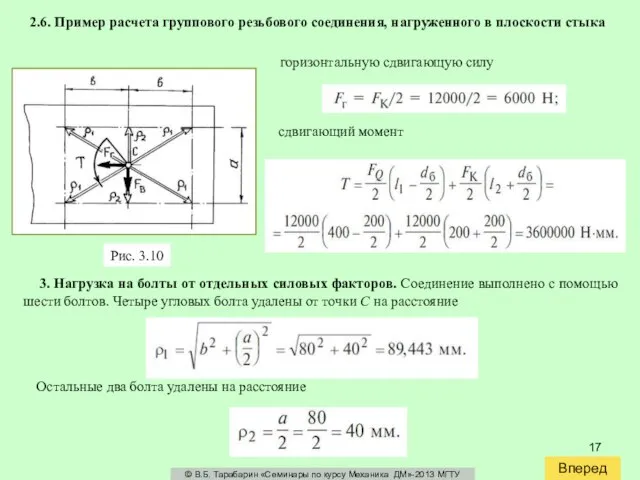
горизонтальную сдвигающую силу
3. Нагрузка на болты от отдельных силовых факторов. Соединение выполнено с помощью шести болтов. Четыре угловых болта удалены от точки C на расстояние
сдвигающий момент
Остальные два болта удалены на расстояние
Рис. 3.10
Слайд 18Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.6. Пример расчета
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.6. Пример расчета

Нагрузка на болты от момента пропорциональна их расстояниям до центра масс. На угловые болты будет действовать сила
где FF1в — вертикальная сила; FF1г — горизонтальная.
В результате сложения сил FF1в и FF1г, имеющих для всех болтов одинаковое направление, получим силу FF1, направленную под углом 45° к вертикали:
Центральные сдвигающие силы Fв и Fг нагружают все шесть болтов одинаковыми силами (рис. 3.11):
Болты, удаленные от центра масс на расстояние ρ2, нагружены меньшей силой FT2 от действия сдвигающего момента.
Рис. 3.11
Слайд 19Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.6. Пример расчета
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.6. Пример расчета

Суммарная сила, действующая на болт,
4. Нагрузка, приходящаяся на наиболее нагруженный болт. Наиболее нагруженным будет тот из угловых болтов, на который действуют составляющие силы, наиболее близкие по направлению. К силе F1F наиболее близка по направлению сила F1T , действующая на болт E (рис. 3.11, б). Эта сила образует с вертикалью угол α:
5. Необходимая по условию несдвигаемости сила затяжки. Сдвига не будет, если сила трения, созданная при затяжке одного болта (см. (3.2)),
где kсц — коэффициент запаса сцепления (запаса по несдвигаемости), kсц = 1,5; F1Σmax — суммарная сдвигающая сила, приходящаяся на наиболее нагруженный болт, F1Σmax = 10498,75 H.
где f — коэффициент трения, принимаем f = 0,2 (см. табл. 3.3); i — число рабочих стыков (по условию i = 1).
Слайд 20Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.6. Пример расчета
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.6. Пример расчета

В соответствии с табл. 3.5 [τ]ср = (0,2...0,3) · σт. Принимаем [τ]ср = 0,25· σт. Согласно табл. 3.2 для класса прочности 5.8 предел текучести σт = 400 МПа. Тогда
Опасными для соединения являются напряжения среза для болта и смятия для болта и стенок отверстия. Условие прочности болта на срез
Принимаем по ГОСТ 7817—80 (cм. табл. 3 приложения 3) болты M12, у которых dc = 13 мм. Необходимая длина болта (cм. рис. 3.3)
По ГОСТ 6402—70 (cм. табл. 6 приложения 3) толщина пружинной нормальной шайбы s = 3,0 мм; по ГОСТ 15521—70 (cм. табл. 4 приложения 3) высота гайки Н =10 мм; запас резьбы над гайкой и высота пяты (ориентировочно) (0,4...0,6)·d;
откуда
Слайд 21Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.6. Пример расчета
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.6. Пример расчета

Проверяем соединение на предотвращение смятия по условию
Принимаем по ГОСТ 7817—80 (cм. табл. 3 приложения 3) l = 40 мм, тогда l — l2 = 22 мм; фаска f = 0,5 мм (cм. рис. 3.3).
Высота поверхности, на которой действуют наибольшие напряжения смятия σсм2,
где Aсм — площадь проекции поверхности смятия; [σ]см — допускаемое напряжение смятия.
Условие прочности не выполняется для материала кронштейна, но выполняется для болтов, у которых [σ]см = 0,4. 400 = 160 МПа. Меняем материал кронштейна на более прочный. Назначаем сталь Ст.6, у которой σт = 300 МПа, [σ]см = 0,4 . 300 = 120 МПа.
Если материал кронштейна по каким-либо причинам нельзя изменить, необходимо увеличить толщину листов кронштейна. После расчета можно определить, что требуемая толщина s1 = s2 = 12 мм. При этом длина болта l = 45 мм, а l — l2 = 22 мм.
Следует отметить, что при постановке болтов без зазора их диаметр существенно уменьшается (М12 вместо М36).
Согласно табл. 3.5 [σ]см = (0,35...0,45)σт, принимаем [σ]см= 0,4·σт. Для болтов σт = 400 МПа, для материала кронштейна (сталь Ст.3) σт = 220 МПа (cм. табл. 1.1).
Расчет ведем по наименее прочному материалу, т. е.
Слайд 22Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.6. Пример расчета
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.6. Пример расчета

где [σ]р — допускаемое напряжение растяжения болта.
Затяжку болтов не контролируют. Предполагаем, что диаметр болта d больше 16 мм. Принимая коэффициент запаса sт= 2,5 (см. табл. 3.4), получаем
Тогда
где σт = 400 МПа — предел текучести болтов класса прочности 5.8 (см. табл. 3.2).
В результате
Пригодны болты М36 по ГОСТ 7796—70 (см. табл. 1 приложения 3), у них d3 = 31,10 мм ( см. табл. 3.1). Предположение о том, что d > 16 мм, подтвердилось.
6. Необходимый диаметр болта из условия прочности затянутого болта. Оно имеет вид
Рассмотрим вариант определения диаметра болтов 5 (см. рис. 3.9) при постановке их без зазора. Конструкция болта показана на рис. 3.3.
Слайд 23Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.7. Пример расчета
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.7. Пример расчета

и в плоскости, перпендикулярной плоскости стыка
Сварной кронштейн (рис. 2.4) прикреплен к бетонной стене с помощью четырех болтов, поставленных с зазором. Детали кронштейна 1 и выполнены из стали Ст.3, сварены угловым швом с катетом шва k =5 мм. Сварка ручная электродом обычного качества. Болты 3 выполнены по классу прочности 4.6. Кронштейн нагружен постоянной силой F = 10000 Н. Размеры: L = 200 мм; δ = 20 мм; a = b = 200 мм; l = g = 150 мм; m = n = 100 мм; s =10мм.
Требуется определить диаметр болтов 3.
Решение. 1. Положение центра масс и действующие на соединение силовые факторы.
Соединение имеет две оси симметрии, центр масс находится на их пересечении в точке О (рис. 3.12). При параллельном переносе внешней силы Fв точку О (рис. 3.13) получаем действующую на соединение центральную сдвигающую силу F = 10000 Н и отрывающий момент M1 = F • L = 10000 • 200 = 2 •106 Н·мм.
Рис. 3.12
Рис. 2.4
Рис. 3.13
Слайд 24Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.7. Пример расчета
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.7. Пример расчета

и в плоскости, перпендикулярной плоскости стыка
2. Необходимая сила затяжки болта F’зат из условия несдвигаемости.
Оно имеет вид
где Fтр — сила трения на стыке; kсц — коэффициент запаса сцепления (запаса по несдвигаемости), kсц > 1,5; F — центральная вншняя сдвигающая сила. Момент M1 перераспределяет давление на стыке, не меняя значение силы трения.
В свою очередь,
где z — число болтов, z =4; f — коэффициент трения, f = 0,4 для стыка металл — бетон (см. табл. 3.3); i — число рабочих стыков, по условию i = 1.
Тогда
3. Необходимая сила затяжки болта F”зат из условия нераскрытия стыка (см. эпюры напряжений). Оно имеет вид
где σmin ст — минимальное напряжение сжатия на стыке после приложения внешней нагрузки.
В свою очередь
Слайд 25Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.7. Пример расчета
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.7. Пример расчета

и в плоскости, перпендикулярной плоскости стыка
Здесь
— напряжение на стыке от затяжки болтов;
Вводя коэффициент запаса k по нераскрытию стыка, получаем
Принимаем k = 1,3, х = 0,75 (стык «металл — бетон»). Тогда
— площадь стыка (без учета отверстий под болты);
— напряжение на стыке от действия момента;
— момент сопротивления стыка относительно нейтральной оси x—x; в нашем случае
Слайд 26Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.7. Пример расчета
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.7. Пример расчета

и в плоскости, перпендикулярной плоскости стыка
4. Принимаем силу затяжки болта Fзат = 9375 Н (большую из двух необходимых).
где Ap — площадь болта по диаметру d3; F Σ вн — суммарная внешняя растягивающая нагрузка, приходящаяся на один болт.
6. Необходимый диаметр болта. Необходимая площадь поперечного сечения болта по диаметру d3
5. Условие прочности болта (3.9) принимает вид
Силы, приходящиеся на болты от действия момента, пропорциональны расстояниям от болтов до нейтральной линии. Максимально нагружены болты, наиболее удаленные от нейтральной линии на расстояние уmах б, дополнительно растягиваемые при действии момента. В нашем случае
где [σ]р = σт/sт допускаемое напряжение для расчета болтов на растяжение; σт — предел текучести материала болта; sт — коэффициент запаса прочности.
Слайд 27Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.7. Пример расчета
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.7. Пример расчета

и в плоскости, перпендикулярной плоскости стыка
Предполагаем, что диаметр болта d менее 30 мм, принимаем sт = 4 (cм. табл. 3.4).
где σ max ст — максимальное напряжение на стыке; [σ]см — допускаемое для бетона напряжение смятия; [σ]см = 1,8 МПа (см. табл. 3.5).
Тогда
7. Заключение по результатам расчета болтов. Пригоден болт М24, по ГОСТ 7796—70 (см. табл. 1 приложения 3) у него d3 == 20,32 мм (см. табл. 3.1). Предположение о том, что d <30мм, подтвердилось.
Для болтов класса прочности 4.6 σт = 240 МПа (cм. табл. 3.2). Тогда
8. Проверка прочности бетонного основания:
Основание достаточно прочное.
Слайд 28Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.7. Пример расчета
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.7. Пример расчета

и в плоскости, перпендикулярной плоскости стыка
Рассмотрим вариант расчета болтов крепления кронштейна к бетонной стене (см. рис. 2.4) в том случае, когда требуется определить класс прочности болтов при известных ограничениях на их диаметр (назначаемых из условий размещения болтов и возможности затяжки их стандартным накидным ключом).
Назначаем болты М16 по ГОСТ 7796—70 (см. табл. 1 приложения 3), у которых диаметр d3 = 13,55 мм (см. табл. 3.1).
Используя приведенные выше в решении примера зависимости, получаем
Решим пример при условии, что диаметр болтов d должен удовлетворять условию:
Максимально возможный диаметр болта
Слайд 29Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.7. Пример расчета
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.7. Пример расчета

и в плоскости, перпендикулярной плоскости стыка
Назначаем коэффициент запаса прочности болта sт = 4 (см. табл. 3.4), тогда пригодными будут болты, имеющие предел текучести материала
Пригодны болты класса прочности 6.8, у которых σт = 480 МПа (см. табл. 3.2).
2.8. Проверка прочности элементов резьбы
Проверка прочности элементов резьбы необходима при использовании: 1) мелких резьб с соотношением (d/P) > 9 (где P — шаг резьбы); 2) низких гаек; 3) материалов корпусов или гаек с малой прочностью (существенно ниже прочности материала болта).
В резьбе возникают напряжения среза и смятия (рис. 3.14).
Смятие для крепежной резьбы не опасно, если ее прочность по срезу обеспечена.
Рис. 3.14
Слайд 30Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
Напряжение среза
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
Напряжение среза

в резьбе болта (винта)
Так как d > D1, то при одинаковых материалах болта и гайки более опасным по срезу витков будет болт. На практике для гаек используют менее прочные материалы, чем для болтов.
При завинчивании винтов и шпилек в корпусные детали для обеспечения равнопрочности резьбы и стержня винта (шпильки) необходима глубина завинчивания, указанная в табл. 3.8.
2.8. Проверка прочности элементов резьбы
в резьбе гайки (корпуса)
где Нг — высота гайки; [τ]срб и [τ]срг — допускаемые напряжения для расчета на срез резьбы болта и гайки (см. табл. 3.5); kб, kг — коэффициенты полноты резьбы для болта и гайки, характеризующие длину линии контакта витков (табл. 3.6); km — коэффициент, учитывающий неравномерность деформирования витков по высоте гайки (табл. 3.7).
Слайд 31Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.8. Проверка
Вперед
© В.Б. Тарабарин «Семинары по курсу Механика ДМ»-2013 МГТУ
2.8. Проверка

 Урок повторения по теме “Световые явления”
Урок повторения по теме “Световые явления” Презентация на тему Изображение пространственных фигур
Презентация на тему Изображение пространственных фигур  Применение различных способов оплат для онлайн продаж в туризме.
Применение различных способов оплат для онлайн продаж в туризме. Волейбол. Двусторонняя игра по правилам
Волейбол. Двусторонняя игра по правилам Презентация на тему Скульптура классицизма
Презентация на тему Скульптура классицизма  Национальный и религиозный состав населения России
Национальный и религиозный состав населения России Система 5С в рационализации рабочего места школьника: основные принципы
Система 5С в рационализации рабочего места школьника: основные принципы Замок Riudabella находится в привилегированном месте у подножия горы, в заповеднике Prades в регионе Конка де Барбера (Испания). Всего в ст
Замок Riudabella находится в привилегированном месте у подножия горы, в заповеднике Prades в регионе Конка де Барбера (Испания). Всего в ст PREZENTATsIYa_Animirovanny_plakat_dlya_obyasnenia_napisania_pismennykh_bukv_russkogo_alfavita
PREZENTATsIYa_Animirovanny_plakat_dlya_obyasnenia_napisania_pismennykh_bukv_russkogo_alfavita Эстония
Эстония Организация приёма в профессиональные образовательные организации Новгородской области
Организация приёма в профессиональные образовательные организации Новгородской области Артериальная гипертензия и беременность
Артериальная гипертензия и беременность  Тысяча слоёв и треуголка императора. Мастер-класс по изготовлению торта Наполеон
Тысяча слоёв и треуголка императора. Мастер-класс по изготовлению торта Наполеон Интегрированный урок математики и истории
Интегрированный урок математики и истории Курсовая работа
Курсовая работа О модернизации учета электроэнергии
О модернизации учета электроэнергии Новогодний ночник
Новогодний ночник ПУБЛИЧНЫЙ ДОКЛАДо состоянии и перспективах развития
ПУБЛИЧНЫЙ ДОКЛАДо состоянии и перспективах развития Школа РосатомаРеализация национальной образовательной инициативы «Наша новая школа» в городах расположения предприятий атомно
Школа РосатомаРеализация национальной образовательной инициативы «Наша новая школа» в городах расположения предприятий атомно Презентация на тему Тема одиночества в лирике Лермонтова
Презентация на тему Тема одиночества в лирике Лермонтова  Планирование заявок на конкурсы для финансирования научно-исследовательских проектов
Планирование заявок на конкурсы для финансирования научно-исследовательских проектов Осенний натюрморт
Осенний натюрморт Школа №4 Жака-Ива Кустопредставляет
Школа №4 Жака-Ива Кустопредставляет Разработка Flash-проектов с использованием Apache Ant
Разработка Flash-проектов с использованием Apache Ant Особенности профессиональной подготовки психологов в России
Особенности профессиональной подготовки психологов в России LEONARDO DICAPRIO
LEONARDO DICAPRIO Презентация на тему Нашествие с запада
Презентация на тему Нашествие с запада «Права пациента в России»
«Права пациента в России»