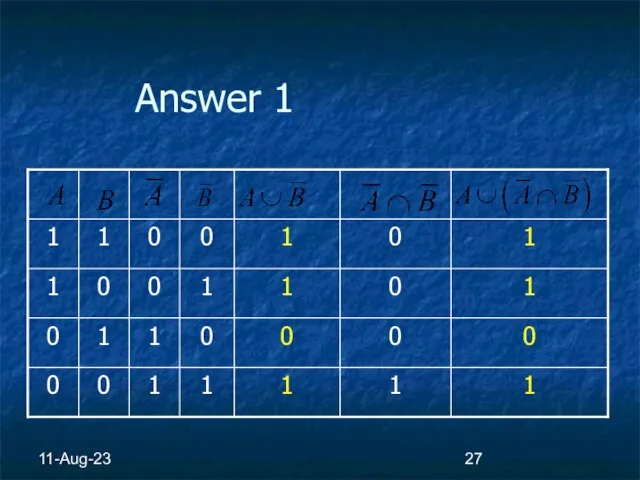
Слайд 211-Aug-23
Seminar 1.
Event Algebra.
Basic Concepts.

Слайд 311-Aug-23
Random Experiment
Suppose that a process that could lead to two or more

different outcomes is to be observed and there is uncertainty beforehand as to which outcome will occur.
Some examples are the following:
A coin is thrown.
A die is rolled.
A consumer is asked which of two products he or she prefers.
Слайд 411-Aug-23
Random Experiment
Some examples are the following:
An item from a set of accounts

is examined by an auditor.
The daily change in an index of stock market prices is observed.
A batch of a chemical produced by a particular process is tested to determine whether it contains more than an allowable percentage of impurity.
Each of these examples involves a random experiment.
Слайд 511-Aug-23
Definition: a random experiment.
A random experiment is a process leading to at

least two possible outcomes with uncertainty as to which will occur
Слайд 611-Aug-23
Random Experiment
In each of the first three experiments listed, it is possible

to specify what outcomes might arise.
If a coin is thrown, the result will be either "head" or "tail."
If a die is rolled, the result will be one of the numbers 1, 2, 3,4, 5, or 6.
A consumer might indicate a preference for one of the products or no preference.
Слайд 711-Aug-23
Definition: Outcomes
The possible outcomes of a random experiment are called the basic

outcomes,
and the set of all basic outcomes is called the sample space
Example : pack of playing cards
Слайд 811-Aug-23
Example
A die is rolled.
The basic outcomes are the numbers 1,

2, 3, 4, 5, 6.
Thus, the sample space is
S = [1, 2, 3, 4, 5, 6]
Here we see that there are six basic outcomes.
No two can occur together, and one of them must occur
Слайд 911-Aug-23
Definition: Events
An event is a set of basic outcomes from the sample

space, and it is said to occur if the random experiment gives rise to one of its constituent basic outcomes
Слайд 1011-Aug-23
Definition:
The intersection of events
Let A and B be two events in

the sample space S.
Their intersection, denoted
is the set of all basic outcomes in S that belong to both A and B.
Hence, the intersection occurs
if and only if both A and B occur.
Слайд 1111-Aug-23
Truth table for intersection of events. Venn diagram
Clearly, a basic outcome will

be in
if and only if it is in both A and B
Слайд 1211-Aug-23
Intersection of events: example
In rolling a die, the outcomes 4 and 6

both belong to the two events
A = "Even number results"
B = "Number at least 4 results”.
Слайд 1311-Aug-23
No intersection
It is possible that events A and B have no common

basic outcomes, in which case the figures will not intersect.
Such events are said to be mutually exclusive
A and B
are mutually exclusive
Слайд 1411-Aug-23
Definition:
mutually exclusive events
If the events A and B have no

common basic outcomes, they are called mutually exclusive and their intersection
is said to be the empty set.
It follows, then, that cannot occur
Слайд 1511-Aug-23
The union of events
When considering jointly several events, another possibility of interest

is that at least one of them will occur.
This will happen if the basic outcome of the random experiment belongs to at least one of the events.
The set of basic outcomes belonging to at least one of the events is called their union.
Слайд 1611-Aug-23
The union of events: example
In the die throw experiment,
the outcomes 2,4,

5, and 6 all belong to at least one of the events
A= "Even number results"
or
B= "Number at least 4 results."
Слайд 1711-Aug-23
Definition: the union of events
Let A and B be two events in

the sample space S.
Their union, denoted ,
is the set of all basic outcomes in S
that belong to at least one of these two events.
Hence, the union occurs
if and only if either A or B (or both) occurs.
Слайд 1811-Aug-23
Truth table for union of events. Venn diagram
It is clear that a

basic outcome will be in
if and only if it is in either A or B (or both).
Слайд 1911-Aug-23
Collectively exhaustive events
A case of special interest concerns a collection of several

events whose union is the whole sample space S.
Since every basic outcome is always contained in S, it follows that every outcome of the random experiment will be in at least one of this collection of events.
These events are then said to be collectively exhaustive
Слайд 2011-Aug-23
Collectively exhaustive events: example
If a die is thrown, the events
A="Result is

at least 3"
and
B="Result is at most 5"
are together collectively exhaustive —
at least one of these two events must occur.
Слайд 2111-Aug-23
The complement of the event
Next, let A be an event, and suppose

our interest is that A not occur.
This will happen if the basic outcome of the random experiment lies in S (as it must)
but not in A.
The set of basic outcomes belonging to the sample space but not to a particular event is called the complement of that event and is denoted
Слайд 2211-Aug-23
The complement of the event
Clearly, the events and are mutually exclusive (no

basic outcome can belong to both) and collectively exhaustive (every basic outcome must belong to one or the other).
Слайд 2311-Aug-23
Definition: the complement of A
Let A be an event in the

sample space S.
The set of basic outcomes of a random experiment belonging to S but not to A
is called the complement of
and is denoted
Слайд 2411-Aug-23
The complement of A: example
If a die is thrown, the complement of

event
A="Result is at least 5"
is event
="Result is at most 4"
Слайд 2511-Aug-23
Truth table for compliment of event. Venn diagram
Clearly, an event occurs
if

and only if an event does not occur
Слайд 2611-Aug-23
Question 1
Prove the statement
with the help of truth tables

Слайд 2811-Aug-23
Question 2
A problem often faced in sociological research is that some of

the questions we would like to ask are so sensitive that many subjects will either refuse to reply or will give a dishonest answer.
One way of attacking this problem
is through the method of
randomized response.
Слайд 2911-Aug-23
Question 2 (continued)
This technique involves pairing the sensitive question with a

nonsensitive question.
For instance, we should want to obtain an information concerning dodging taxes.
So we might create the following pair:
(a) Have you purposely evaded taxes in the last 12 months? (sensitive question)
(b) Have you obtained a “head” in the trial of coin tossing? (nonsensitive question)
Слайд 3011-Aug-23
Question 2 (continued)
Subjects are asked to flip a coin and then

to answer question
(a) if the result is "head"
and flip a coin once again and answer (b) otherwise.
Since the investigator cannot know which question is answered, it is hoped that honest responses will be obtained in this way.
Слайд 3111-Aug-23
Question 2 (continued)
The nonsensitive question is one for which the investigator

already has information.
Thus, in our example, the investigator knows what proportion of “tails” is .
Слайд 3211-Aug-23
Question 2 (continued)
Now, we define the following events:
A : Subject answers

"yes."
: Subject answers sensitive question.
: Subject answers nonsensitive question.
Clearly, the events and
are mutually exclusive and collectively exhaustive.
Слайд 3311-Aug-23
Question 2 (continued)
Thus, the conditions of result (3) are satisfied, and it

follows that the events
Subject both responds "yes" and has answered the sensitive question
: Subject both responds "yes" and has answered the nonsensitive question
are mutually exclusive.
Furthermore, their union must be the event A; that is
Слайд 3411-Aug-23
Question 2 (continued)
“head”
“tail”
sensitive question
yes
no
yes
no
nonsensitive question
“head”
“tail”

Слайд 3511-Aug-23
Question 2 (continued)
Let the proportion of population evaded taxes be 20%. What

is the proportion of “yes” answers in our survey?
In real survey 30% of people answer “yes”. What is the proportion of people dodging taxes?
Слайд 3611-Aug-23
What is Probability?
Suppose that a random experiment is to be carried out

and we are interested in the chance of a particular event's occurring.
The concept of probability is intended to provide a numerical measure for the likelihood of an event's occurrence
Слайд 3711-Aug-23
What is Probability?
Probability is measured on a scale from 0 to 1.
At

the extremes of this range, a probability of 0 implies that the event is impossible (it is certain not to occur),
whereas a probability of 1 implies that the event is certain to occur.
For uncertain events, we want to attach a probability between 0 and 1 such that the more likely the event is to occur, the higher the probability
Слайд 3811-Aug-23
What is Probability?
In practice, such ideas are frequently met.
It is known that

rain is more likely under certain meteorological conditions than others.
An experienced manager may judge that one product is more likely to achieve substantial market penetration than another.
Слайд 3911-Aug-23
What is Probability?
To take a very simple example, suppose a coin is

thrown.
The statement "The probability that a head results is M" may be viewed through two distinct ideas — relative frequency and subjective probability
Слайд 4011-Aug-23
Relative Frequency
Suppose that a random experiment can be replicated in such a

way that,
after each trial, it is possible to return to the initial state and repeat the experiment so that the resulting outcome is unaffected by previous outcomes.
For example, a coin or die can be thrown repeatedly in this way.
Слайд 4111-Aug-23
Relative Frequency
If some number N of experiments is conducted and the event

A occurs in of them
( clearly depending on N),
we have
Слайд 4211-Aug-23
Relative Frequency
Now, if N is very large, we would not expect much

variation in the proportion
as N increases;
that is, the proportion of occurrences of A will remain approximately constant.
This notion underlies the relative frequency concept of probability
Слайд 4311-Aug-23
Definition: Relative Frequency
Let be the number of occurrences of event A in

N repeated trials.
Then, under the relative frequency concept of probability, the probability that A occurs is the limit of the ratio as the number of trials N becomes infinitely large
Слайд 4411-Aug-23
Relative Frequency
Under this definition, if we say
"The probability of a head

resulting from a single throw of a coin is "
we mean that if the coin is thrown repeatedly, the proportion of heads resulting will get very close to as the number of trials gets very large
The relative frequency notion provides a convenient framework for thinking about probability, but it does involve conceptual difficulties
Слайд 4511-Aug-23
Subjective Probability
An alternative view, which does not depend on the notion of

repeatable experiments, regards probability as a personal subjective concept, expressing an individual's degree of belief about the chance that an event will occur.
One way to understand this idea is in terms of fair bets
Слайд 4611-Aug-23
Subjective Probability
For example, if I assert that the probability of a head

resulting from the throw of a coin is , what I have in mind is that the coin appears to be perfectly fair and that the throw is just as likely to produce a head as a tail.
In assessing this subjective probability, I am not necessarily thinking in terms of repeated experimentation but am concerned with only a single throw of the coin.
Слайд 4711-Aug-23
Subjective Probability
My subjective probability assessment implies that I would view as fair

a bet in which I had to pay $1 if the result was tail and would receive $1 if the result was head.
If I were to receive more than $1 if the throw yielded a head, I would regard the bet as in my favor.
Слайд 4811-Aug-23
Subjective Probability
Similarly, if I believe that the probability of a horse's winning

a particular race is .4, I am asserting the personal view that there is a 40-60 chance of its winning.
Given this belief, I would regard as fair a bet in which I lost $2 if the horse did not win and gained $3 if it did
Слайд 4911-Aug-23
Subjective Probability
It should be emphasized that subjective probabilities are personal;
there is

no requirement that different individuals considering the same event should arrive at the same probabilities.
In the coin-throwing example, most people will conclude that the appropriate probability for a head is
Слайд 5011-Aug-23
Subjective Probability
However, an individual with more information about the coin in question

might believe otherwise.
In the example of the horse race, it is likely that two bettors will reach different subjective probabilities.
They may not, for example, have the same information, and even if they do, they might not interpret it in the same way.
Слайд 5111-Aug-23
Subjective Probability
It is certainly clear that individual investors do not all hold

the same views on the likely future behavior of the stock market!
Their subjective probabilities might be thought of as depending on the knowledge they have and the way they interpret it

















































 Английский этикет
Английский этикет животные
животные Презентация на тему Человек прямоходящий (1 класс)
Презентация на тему Человек прямоходящий (1 класс) Строение солнечной системы
Строение солнечной системы Псалом 117, мессианский
Псалом 117, мессианский Часть 2.
Часть 2. Психология общения
Психология общения  Сибирский федеральный университет
Сибирский федеральный университет Мастер-класс для HR-ов на тему АССЕССМЕНТ:массовый (mass) и экспресс (express)(на примере проекта фонда В.Пинчука «ZAVTRA.UA»)
Мастер-класс для HR-ов на тему АССЕССМЕНТ:массовый (mass) и экспресс (express)(на примере проекта фонда В.Пинчука «ZAVTRA.UA») Творческая лаборатория. Педагогический проект по теме: «Сценическое воплощение литературного произведения». Автор проекта – уч
Творческая лаборатория. Педагогический проект по теме: «Сценическое воплощение литературного произведения». Автор проекта – уч Strategiia_i_taktika_upravleniia_biznesom_v_usloviiakh_konkurentsii_11507040
Strategiia_i_taktika_upravleniia_biznesom_v_usloviiakh_konkurentsii_11507040 Особенности организации управления в Вене
Особенности организации управления в Вене Праздники и традиции Великобритании
Праздники и традиции Великобритании Булат Окуджава
Булат Окуджава Давление твёрдых тел 7 класс
Давление твёрдых тел 7 класс Психологический климат в семье
Психологический климат в семье Внеурочная деятельность как составляющая образовательной деятельности
Внеурочная деятельность как составляющая образовательной деятельности Святковий концерт до Дня Святого МИколая презентували учні 3-А класу Бершадської ЗОШ №3
Святковий концерт до Дня Святого МИколая презентували учні 3-А класу Бершадської ЗОШ №3 Моктесума
Моктесума Удмуртская кухня
Удмуртская кухня Тренинг общения
Тренинг общения Объёмы тел
Объёмы тел Презентация на тему Страницы истории 19 века (4 класс)
Презентация на тему Страницы истории 19 века (4 класс) Форсайт. Взгляд в будущее
Форсайт. Взгляд в будущее Вариант 1 1. Органические соединения образуются в хлоропластах листьев: а. из воды и кислорода; в. хлорофилла; б. воды и
Вариант 1 1. Органические соединения образуются в хлоропластах листьев: а. из воды и кислорода; в. хлорофилла; б. воды и Антикафе Чтец
Антикафе Чтец «Золотое» сечение в архитектуре русских храмов
«Золотое» сечение в архитектуре русских храмов Урок 3 (Анимация. Движение по криволинейной)
Урок 3 (Анимация. Движение по криволинейной)