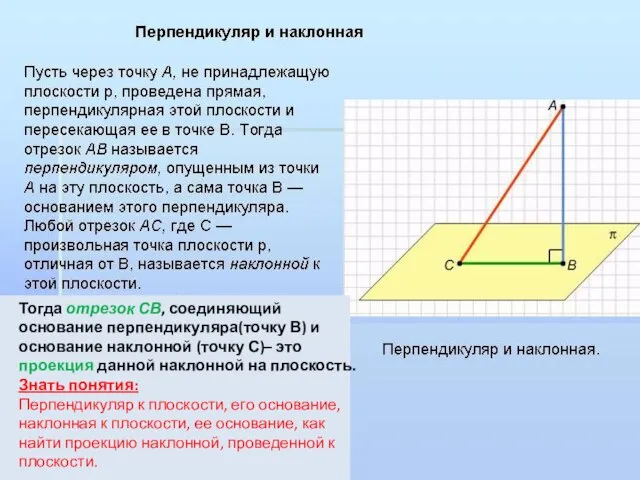
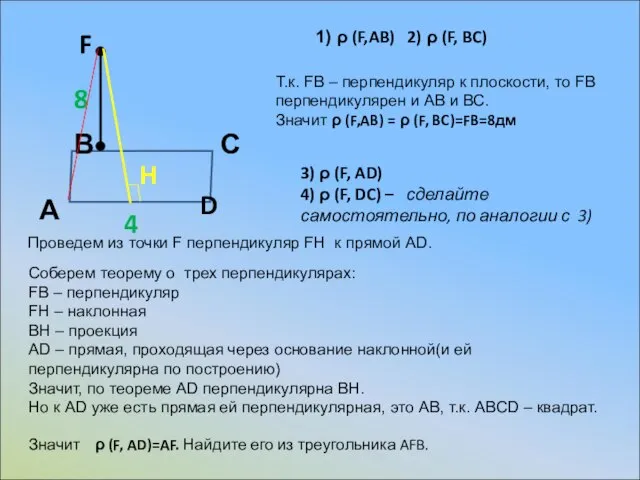
то FB перпендикулярен и АВ и ВС.
Значит ρ (F,AB) = ρ (F, BC)=FB=8дм
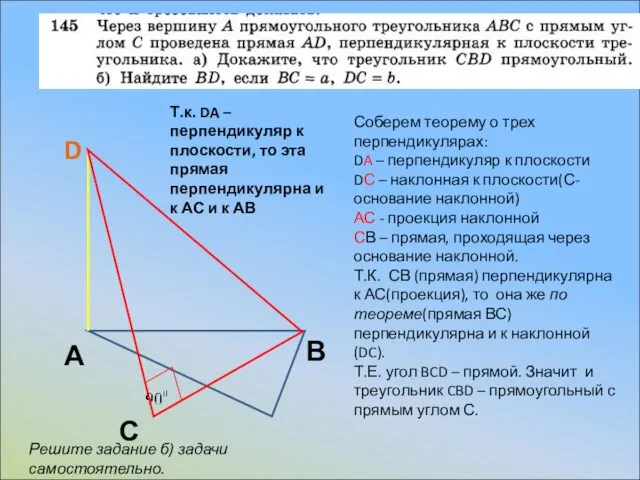
D
3) ρ (F, AD)
4) ρ (F, DC) – сделайте самостоятельно, по аналогии с 3)
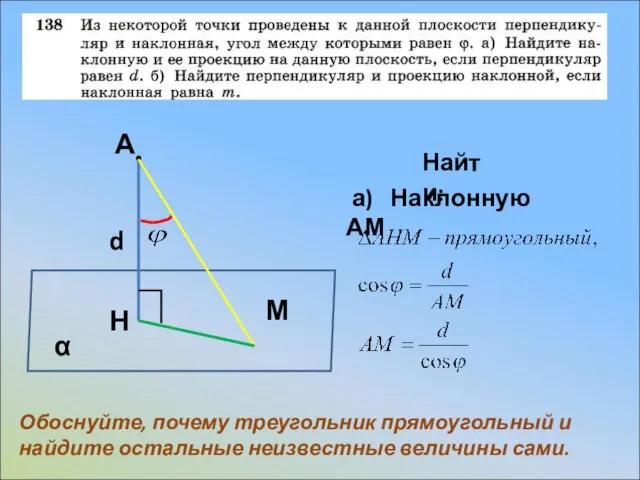
Проведем из точки F перпендикуляр FH к прямой AD.
H
Соберем теорему о трех перпендикулярах:
FB – перпендикуляр
FH – наклонная
BH – проекция
AD – прямая, проходящая через основание наклонной(и ей перпендикулярна по построению)
Значит, по теореме AD перпендикулярна BH.
Но к AD уже есть прямая ей перпендикулярная, это АВ, т.к. ABCD – квадрат.
Значит ρ (F, AD)=AF. Найдите его из треугольника AFB.
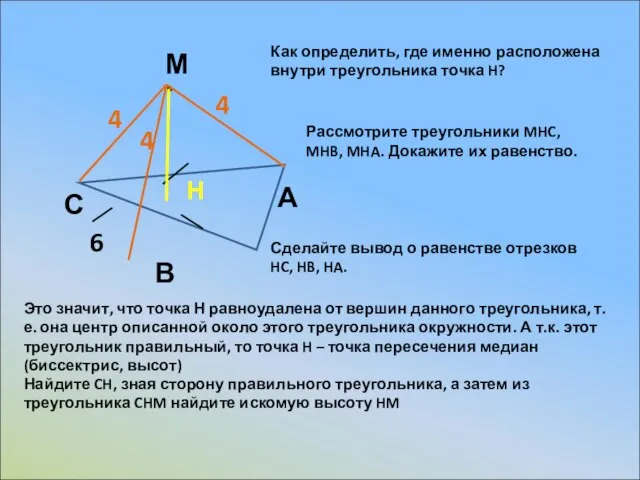



 Искусство эпохи возрождения в Италии
Искусство эпохи возрождения в Италии Передача оценки аудио в периметр ЕРЦ по Волгограду
Передача оценки аудио в периметр ЕРЦ по Волгограду Фитнес для людей с ограниченными возможностями
Фитнес для людей с ограниченными возможностями Особенности локализации в области e-Learningна примере проектов NETg и MicrosoftКомпания «Логрус»Май 2007
Особенности локализации в области e-Learningна примере проектов NETg и MicrosoftКомпания «Логрус»Май 2007 Значение физической культуры и спорта в жизни человека
Значение физической культуры и спорта в жизни человека НАНОТЕХНОЛОГИИ
НАНОТЕХНОЛОГИИ Проект «Программа развития образовательного учреждения»
Проект «Программа развития образовательного учреждения» Понятие о правоотношениях в сфере физической культуры и спорта. Билет 2
Понятие о правоотношениях в сфере физической культуры и спорта. Билет 2 Молодежный билет
Молодежный билет Античная философия
Античная философия Организационное собрание с первокурсниками Академии архитектуры и искусств Южного федерального университета 1 сентября 2021
Организационное собрание с первокурсниками Академии архитектуры и искусств Южного федерального университета 1 сентября 2021 Качественное исследование. Понятие, сущность, особенности
Качественное исследование. Понятие, сущность, особенности Психология цвета
Психология цвета Универсальные меры предосторожности
Универсальные меры предосторожности RU TV
RU TV Великие химики
Великие химики Виды памяти, вытесняющие статическую память
Виды памяти, вытесняющие статическую память Оценка эффективности использования комплекса маркетинговых инструментов в аптечном пространстве Олег Фельдман, КОМКОН-Фарма, Г
Оценка эффективности использования комплекса маркетинговых инструментов в аптечном пространстве Олег Фельдман, КОМКОН-Фарма, Г Пошив спортивной формы и экипировки для всех видов спорта с нанесением символики
Пошив спортивной формы и экипировки для всех видов спорта с нанесением символики Дружок
Дружок Карнавал животных
Карнавал животных Метод подстановки решения систем уравнений
Метод подстановки решения систем уравнений Формы знаний о мире
Формы знаний о мире Janssen_digital_diary_v.04
Janssen_digital_diary_v.04 Поисковый спам как способ заработка Иван Васильевич
Поисковый спам как способ заработка Иван Васильевич Комплексный анализ каузативных конструкций в итальянском языке
Комплексный анализ каузативных конструкций в итальянском языке What can he do?
What can he do? Алкоголизм и его влияние на развитие здоровой личности
Алкоголизм и его влияние на развитие здоровой личности