Реология и гидравлика буровых растворов

Задачи:
Узнать различные реологические модели и режимы течения жидкостей
Определять параметры буровых растворов и их влияние на гидравлические характеристики
Определять источники потерь давления и их влияние на гидравлические характеристики
Оптимизировать гидравлику на долоте с помощью понятий гидравлической мощности и силы воздействия потока на забой
После изучения данной темы вы сможете:

Реология
Режимы течения
Реологические модели
Ньютоновская модель
Бингамовская модель
Степенная модель
Модифицированная степенная модель
Гидродинамические расчеты
Оптимизация гидравлики долота
Программа

Реология
Реология (от греч. ρέος, «течение, поток») – раздел физики, изучающий деформации и текучесть вещества (Wikipedia).
Реология – наука о поведении различных текучих и пластичных тел при механическом нагружении (MI Drilling Fluids Engineering Manual).
В твердых веществах Напряжение (Stress) вызывает Деформацию (Strain)
В жидких веществах Напряжение (Stress) вызывает Сдвиг /Расход (Rate)

Зачем изучать реологию?
Как раствор выносит шлам из скважины
Как раствор чистит поверхность долота от выбуриваемой породы
Каковы потери давления в системе
Как буровой раствор ведет себя в при тех режимах течения, которые наблюдаются в скважине
Нам необходимо предсказать:
Другими словами, нам необходимо понимать гидравлику буровых жидкостей

Вязкость
Вязкостью в широком смысле может быть названа способность среды сопротивляться течению.
В такой трактовке термин «вязкость» является наиболее общей характеристикой текучести жидкости и может аккумулировать в себе не только собственно вязкостные свойства жидкостей, но и их пластические и тиксотропные свойства.
Вот почему в зависимости от метода определения существуют различные показатели вязкости (и соответствующие термины, относящиеся к вязкости).

Термины, определяющие вязкость раствора
M-I SWACO использует следующие термины, связанные с вязкостью и другими реологическими характеристиками буровых растворов:
Условная вязкость /Funnel viscosity/ (сек/кварта или сек/л)
Эффективная вязкость /Effective viscosity/ (сП или мПа*сек)
Кажущаяся вязкость /Apparent viscosity/ (cП или мПа*сек)
Пластическая вязкость /Plastic viscosity/ (сП или мПа*сек)
Предельное динамическое напряжение сдвига /Yield point/ (фунт/100 фут2 или дПа)
Коэффициент консистенции /Consistency index/ (дПа*сn или дн*сn/см2)
Показатель нелинейности /Power Low index/ (безразмерная величина)
Вязкость при низкой скорости сдвига /Low-Shear-Rate Viscosity/ (сП или мПа*сек)
Динамическое напряжение сдвига при низкой скорости сдвига / LSRYP (фунт/100фут2)
Предельное статическое напряжение сдвига /Gel strengths/ (фунт/100 фут2 или дПа).

Реологические модели
Реология изучает связи между деформациями (или скоростями деформаций) с действующими в жидкости напряжениями, математически выражая эти связи реологическими молелями.
В зависимости от поведения жидкости в движении применительно к буровым растворам рассматривают четыре реологические модели:
Ньютоновская модель
Бингамовская модель
Степенная модель
Модифицированная степенная модель

Реологические модели и расчет гидродинамики
В свою очередь реологические модели используются в решении задач гидродинамики (изучающей движение жидкостей и воздействие их на обтекаемые ими тела).
Реология и гидродинамика – это две взаимосвязанные части механики жидкостей
Применительно к буровым растворам их механические свойства должны быть количественно выражены параметрами соответствующих реологических моделей;
А затем эти параметры могут быть использованы для решения инженерных гидродинамических задач при бурении скважин.

Реологические свойства
Реологические свойства конкретных жидкостей устанавливаются экспериментальными методами.
Измеряя реологические характеристики бурового раствора, можно определить, как этот раствор будет течь при различной температуре, давлении и скорости сдвига.

Реологические модели
Пробковый
Ламинарный
Переходный
Турбулентный
В каждой модели существует 4 различных режима течения:

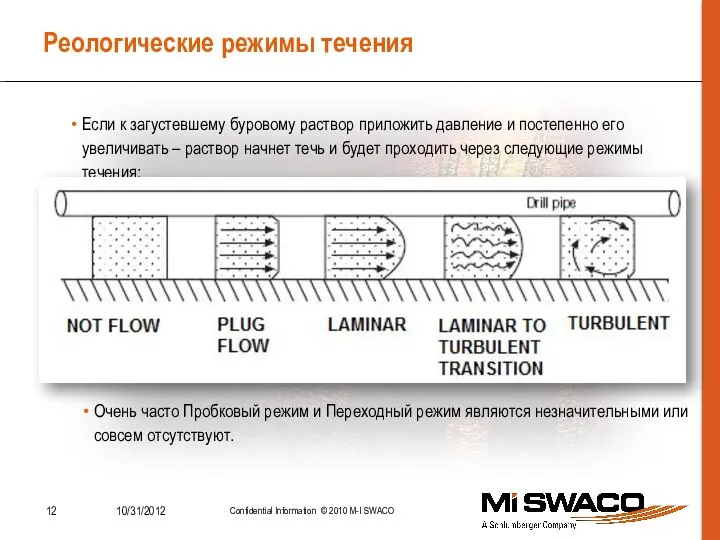
Реологические режимы течения
Если к загустевшему буровому раствор приложить давление и постепенно его увеличивать – раствор начнет течь и будет проходить через следующие режимы течения:
Очень часто Пробковый режим и Переходный режим являются незначительными или совсем отсутствуют.

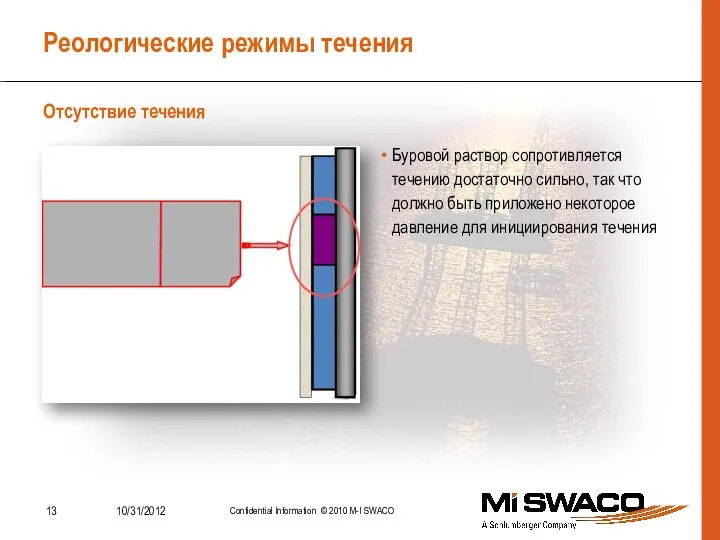
Реологические режимы течения
Отсутствие течения
Буровой раствор сопротивляется течению достаточно сильно, так что должно быть приложено некоторое давление для инициирования течения

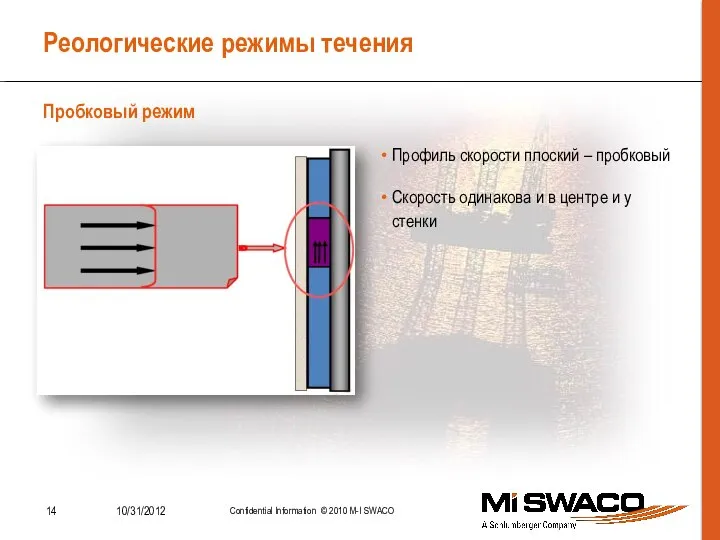
Реологические режимы течения
Пробковый режим
Профиль скорости плоский – пробковый
Скорость одинакова и в центре и у стенки

Реологические режимы течения
В пробковом режиме жидкость движется как единое однородное тело, подобно твердому телу
Пробковый режим характерен для вертикальных стволов большого диаметра
Он также отмечается в растворах для забуривания скважин, например, в неутяжеленных, флокулированных бентонитовых системах
Эти системы отличаются достаточно высокой вязкостью
Ярко выраженный плоский профиль течения с отличной выносящей способностью
Пробковый режим не вызывает расширения ствола
Очень редкое явление в обычных условиях бурения
Характеристики пробкового режима течения:

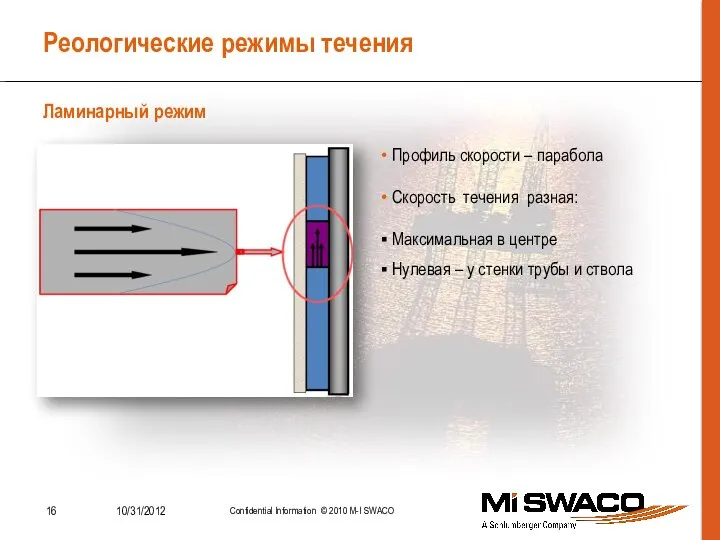
Реологические режимы течения
Ламинарный режим
Профиль скорости – парабола
Скорость течения разная:
Максимальная в центре
Нулевая – у стенки трубы и ствола

Характеристики ламинарного режима
Распространенный режим в обычных условиях бурения, но чаще отмечается в затрубном пространстве, чем внутри труб
Параллельные линии течения, но неплоский профиль скорости течения
Профиль скорости меняется от очень высокой (в центре) до минимальной (по краям)
Отмечается в растворах как с очень высокой, так и с очень низкой вязкостью

Характеристики ламинарного режима
Переходный режим – это режим между ламинарным и турбулентным течением жидкости.
Течение жидкости уже не ламинарное, но еще не полностью турбулентное.
Ширина переходного режима зависит от неньютоновских свойств жидкости и от используемой реологической модели

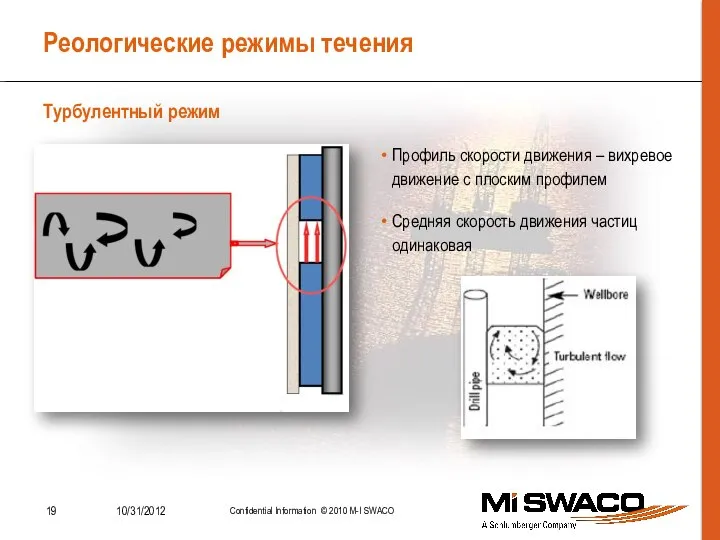
Реологические режимы течения
Турбулентный режим
Профиль скорости движения – вихревое движение с плоским профилем
Средняя скорость движения частиц одинаковая

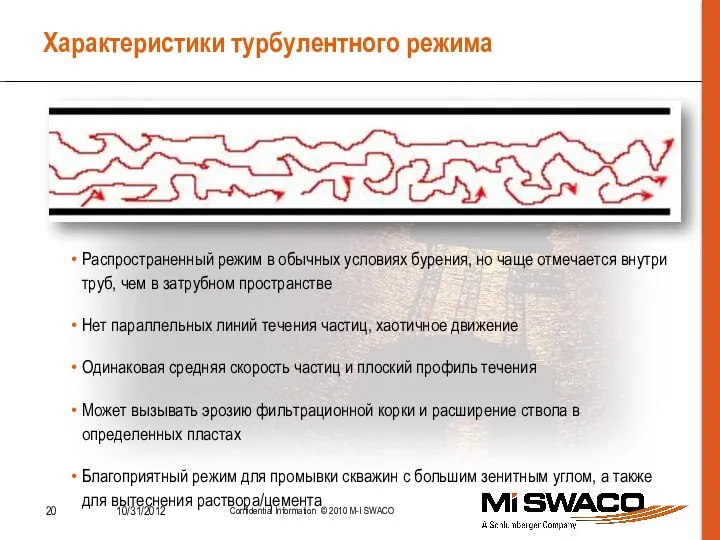
Характеристики турбулентного режима
Распространенный режим в обычных условиях бурения, но чаще отмечается внутри труб, чем в затрубном пространстве
Нет параллельных линий течения частиц, хаотичное движение
Одинаковая средняя скорость частиц и плоский профиль течения
Может вызывать эрозию фильтрационной корки и расширение ствола в определенных пластах
Благоприятный режим для промывки скважин с большим зенитным углом, а также для вытеснения раствора/цемента

Режимы течения бурового раствора в скважине
Важное значение для развития гидравлики имело физическое обоснование режимов движения жидкости Освальдом Рейнольдсом (1842 - 1912)
В 1883 г. Рейнольдсом были произведены опыты, в которых рассматривался механизм различных видов движения.
При разных скоростях движения удалось установить зависимость между скоростью, геометрическими размерами стенок и степенью вязкости жидкости.
Ламинарный или турбулентный режим?

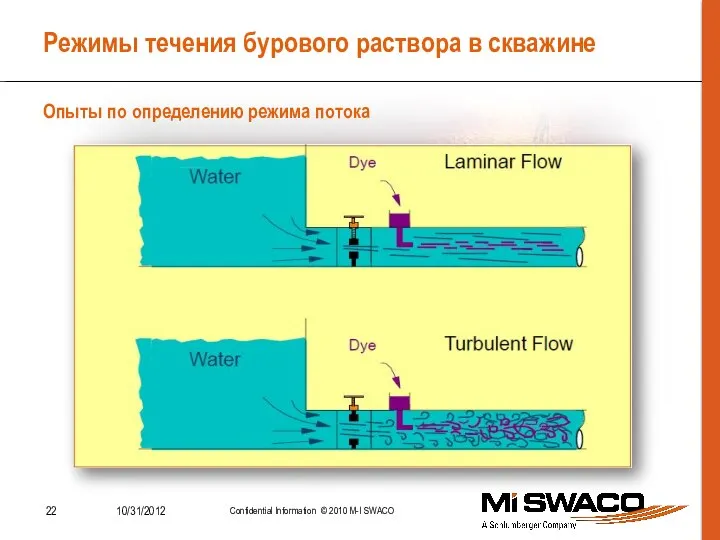
Режимы течения бурового раствора в скважине
Опыты по определению режима потока

Режимы течения бурового раствора в скважине
безразмерный параметр, используемый для определения режима течения жидкости.
В бюллетене API 13D третье издание от 1 июня 1995 г. «Recommended Practice on the Rheology and Hydraulics of Oil-Well Drilling Fluids» рекомендуется, что при числе Re < 2100 реализуется ламинарный режим течения раствора, а при Re > 2100 реализуется турбулентный режим течения раствора.
Число Рейнольдса (Re) –
Общая формула для определения числа Рейнольдса:
где:
V – скорость потока, фут/мин;
D – диаметр, дюйм;
ρ – плотность жидкости, фунт/галлон;
μ – вязкость жидкости, сП

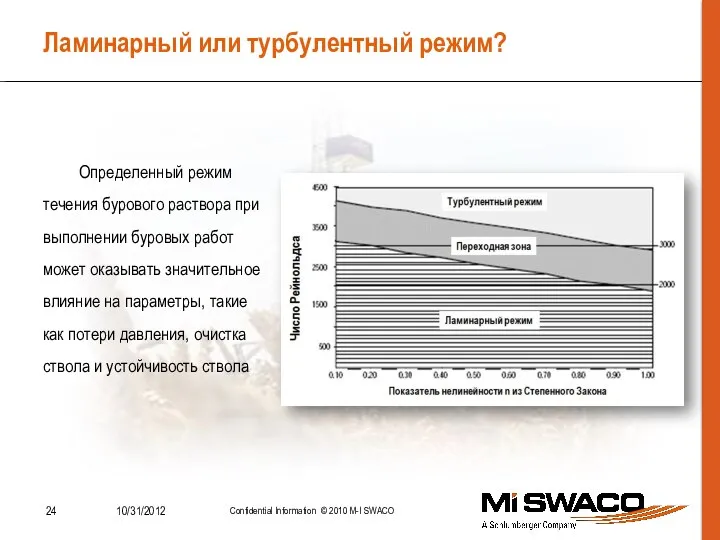
Определенный режим течения бурового раствора при выполнении буровых работ может оказывать значительное влияние на параметры, такие как потери давления, очистка ствола и устойчивость ствола
Ламинарный или турбулентный режим?

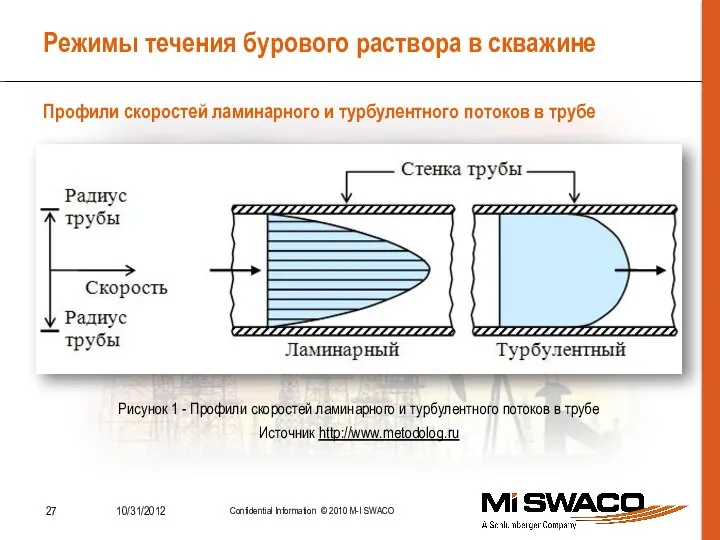
Режимы течения бурового раствора в скважине
Характеризуется слоистым движением жидкости без перемешивания частиц и наблюдается:
Ламинарный режим
в порах грунта при движении подземных вод;
в капиллярных трубках;
в потоках малого размера;
при движении по трубам нефти и масел.

Режимы течения бурового раствора в скважине
Характеризуется перемешиванием частиц жидкости, которые, кроме поступательного движения с большими скоростями, приобретают вращательное движение.
При турбулентном режиме наблюдается пульсация скорости, т. е. изменение скорости по величине и направлению.
Турбулентный режим отмечается:
Турбулентный режим
при движении жидкости по трубам;
в реках и каналах;
в подземных водах около скважин при откачке воды;
в карстовых образованиях, по трещинам и в горных выработках.

Режимы течения бурового раствора в скважине
Профили скоростей ламинарного и турбулентного потоков в трубе
Рисунок 1 - Профили скоростей ламинарного и турбулентного потоков в трубе
Источник http://www.metodolog.ru

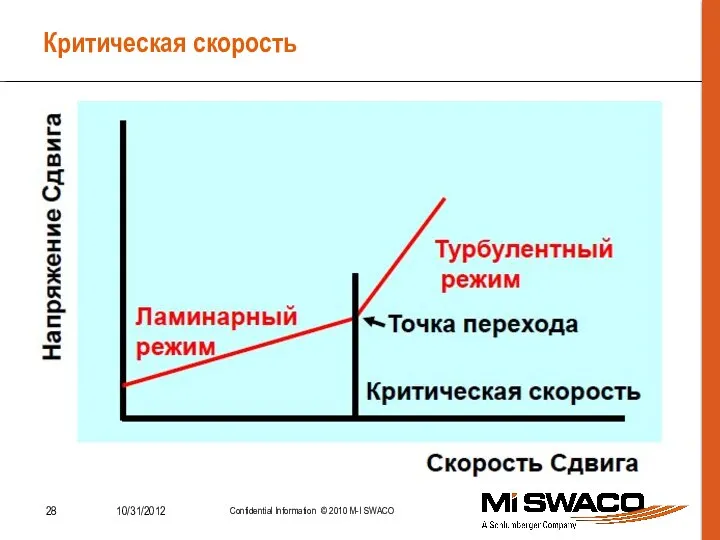
Критическая скорость

Реология
Режимы течения
Реологические модели
Ньютоновская модель
Бингамовская модель
Степенная модель
Модифицированная степенная модель
Гидродинамические расчеты
Оптимизация гидравлики долота
Программа

Реологическая модель
Реологические модели разработаны для описания зависимости давления, необходимого для достижения определенного расхода при данной вязкости и плотности жидкости.
Их основная задача – сопоставить реальное поведение жидкости с прогнозируемой моделью для:
Низких скоростей, когда вязкость не является константой
Средних скоростей, при которых скорость и напряжение пропорциональны (ламинарный режим)
Высоких скоростей с хаотичным потоком (турбулентный режим)
Невозможно создать математическую модель реологии жидкости в турбулентном режиме. В этом случае потери давления устанавливаются эмпирическими уравнениями

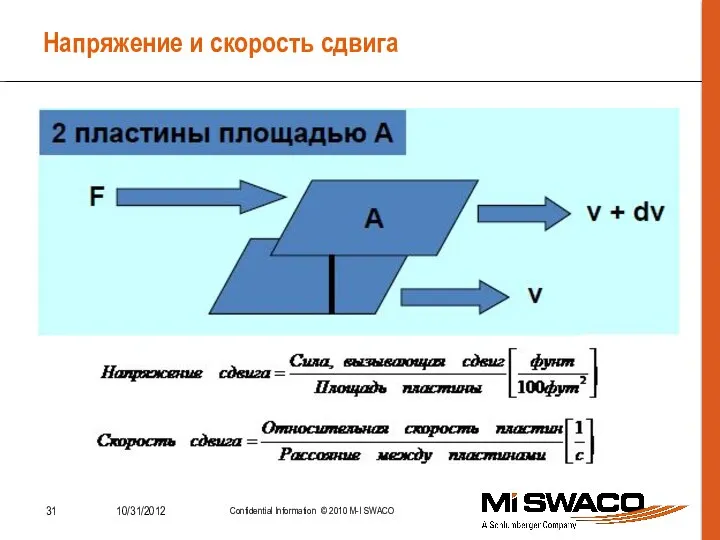
Напряжение и скорость сдвига

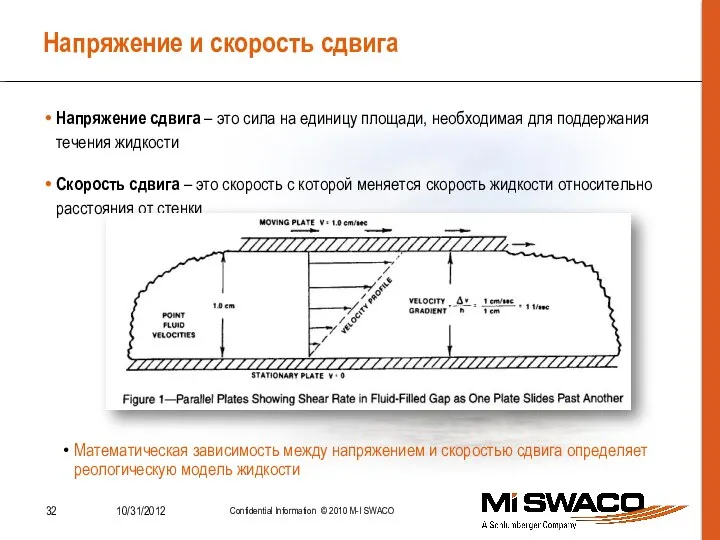
Напряжение и скорость сдвига
Напряжение сдвига – это сила на единицу площади, необходимая для поддержания течения жидкости
Скорость сдвига – это скорость с которой меняется скорость жидкости относительно расстояния от стенки
Математическая зависимость между напряжением и скоростью сдвига определяет реологическую модель жидкости

Переменные реологических моделей
– это градиент скорости сдвигового течения
где:
Скорость сдвига (Shear Rate)
∆V – разность скоростей сдвигаемых относительно друг друга слоев жидкости;
∆ x – расстояние между слоями
[Скорость сдвига] = с-1

Переменные реологических моделей
где:
Напряжение сдвига (Shear Stress)
∆F – сила сопротивления сдвигу, действующая в направлении течения;
∆ S – площадь поверхности сдвигаемых слоев жидкости
[Напряжение сдвига] = Па (lbs/100ft2)
1 lbs/100ft2 = 4,79 дПа

Эффективная вязкость
Эффективня вязкость (μе) – отношение напряжения сдвига к скорости сдвига:
Если эффективная вязкость жидкости не меняется при изменении скорости сдвига, такая жидкость называется ньютоновской /Newtonian fluid/.
В противном случае жидкость называется неньютоновской /non-Newtonian fluid/.
Как правило, эффективная вязкость буровых растворов уменьшается с увеличением скорости сдвига, поэтому данные растворы относятся к неньютоновским жидкостям.

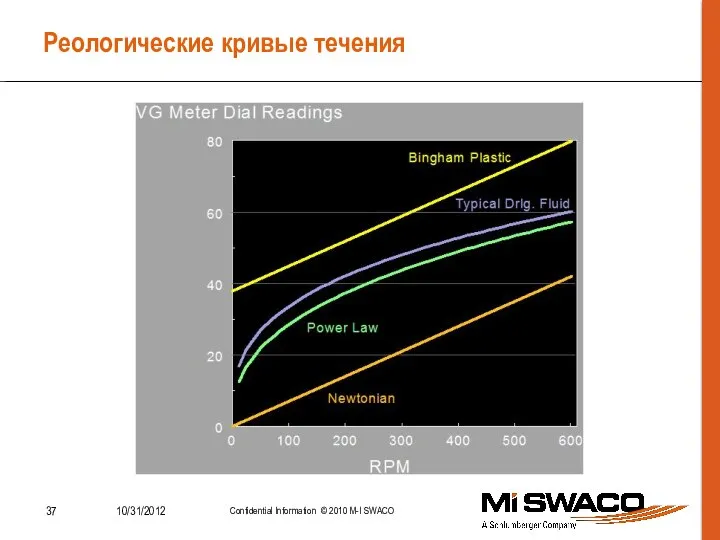
Реологические модели
Ньютоновская модель
Бингамовская модель вязкопластичной жидкости (в русскоязычной литературе – модель Шведова-Бингама)
Степенной закон (модель Оствальда-де Ваале)
Модифицированный степенной закон (модель Гершеля-Балкли).
Реологические свойства буровых растворов описывают следующие модели:

Реологические кривые течения

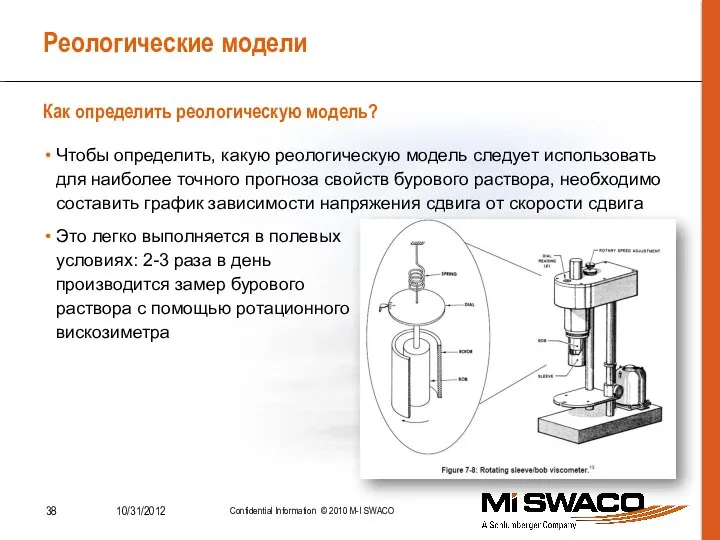
Реологические модели
Чтобы определить, какую реологическую модель следует использовать для наиболее точного прогноза свойств бурового раствора, необходимо составить график зависимости напряжения сдвига от скорости сдвига
Как определить реологическую модель?
Это легко выполняется в полевых условиях: 2-3 раза в день производится замер бурового раствора с помощью ротационного вискозиметра

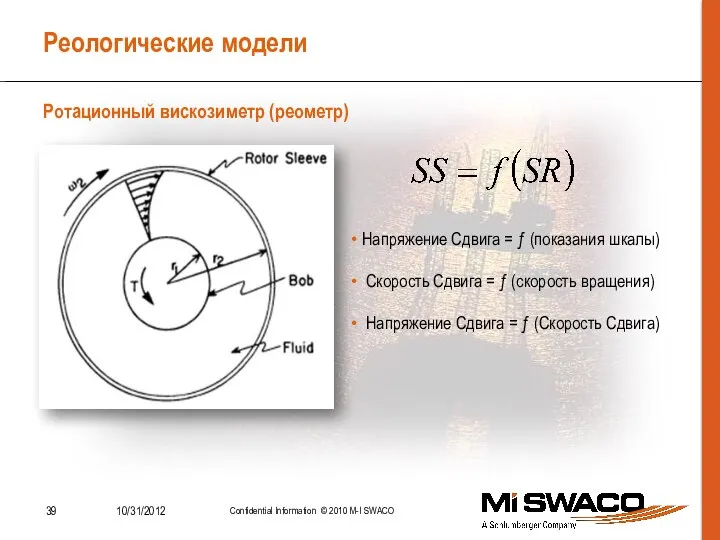
Реологические модели
Ротационный вискозиметр (реометр)
Напряжение Сдвига = ƒ (показания шкалы)
Скорость Сдвига = ƒ (скорость вращения)
Напряжение Сдвига = ƒ (Скорость Сдвига)

Реологические модели
Конструкция реометра такова, что напряжение сдвига (в фунт/100фут2 ) равно коэффициенту пружины, умноженному на показание дисковой шкалы. Коэффициент пружины равен 1.0678.
Показание шкалы х 1.0678 = фунт/100фут2
Показание шкалы х 5.11 = дин/см2 (5.11=1.0678 х 4.79)
Дисковая шкала и напряжение сдвига

Реологические модели
Конструкция вискозиметра такова, что разница в скорости вращения цилиндра, поделенная на ширину зазора и умноженная на коэффициент, дает значение Скорости Сдвига
Стержень настроен таким образом, что если об/мин. умножить на коэффициент 1.7, – получим величину в [сек -1 ]
Скорость вращения и скорость сдвига
Об/мин. x 1.703 = сек -1

Скорости сдвига в различных элементах циркуляционной системы
Емкости 1 - 5 c-1
Кольцевое пространство 10 - 500 c-1
Бурильные трубы 100 - 700 c-1
УБТ 700 - 3000 c-1
Долото 10000 -100000 c-1

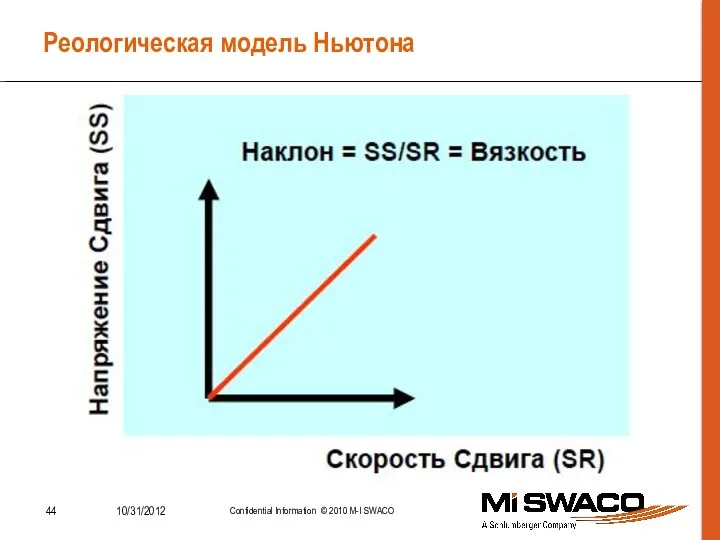
Реологическая модель Ньютона
[Вязкость] = Па*с (Пз)
1 мПа*с = 1 сПз
Модель Ньютона описывает реологические свойства многих низкомолекулярных жидкостей (воды, спиртов, минеральных масел и т.п.), вязкость которых зависит только от температуры и давления
Вязкость ньютоновской жидкости µ не зависит от скорости сдвига

Реологическая модель Ньютона

Упражнение №1
Ньютоновская модель
Задача:
Площадь верхней пластины = 20 см2
Расстояние между пластинами = 1 см
Сила, необходимая для сдвига верхней пластины со скоростью 10 см/с, равна 100 дин.
Какова Вязкость флюида?

Упражнение №1
Решение

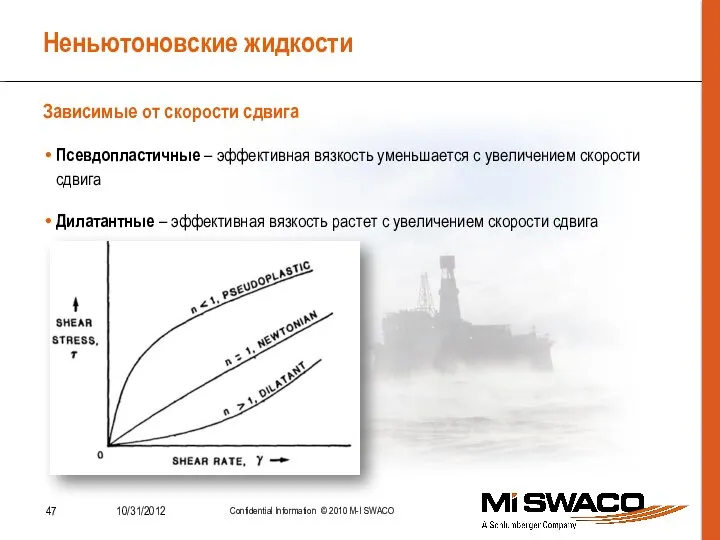
Неньютоновские жидкости
Псевдопластичные – эффективная вязкость уменьшается с увеличением скорости сдвига
Дилатантные – эффективная вязкость растет с увеличением скорости сдвига
Зависимые от скорости сдвига

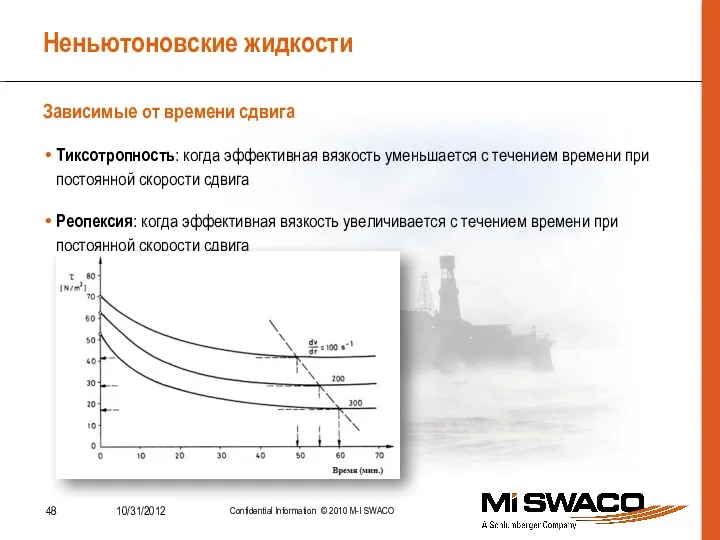
Неньютоновские жидкости
Тиксотропность: когда эффективная вязкость уменьшается с течением времени при постоянной скорости сдвига
Реопексия: когда эффективная вязкость увеличивается с течением времени при постоянной скорости сдвига
Зависимые от времени сдвига

Бингамовская модель вязкопластичной жидкости
Модель Бингама описывает реологические свойства жидкости, течение которой возмодно только при напряжениях сдвига (SS), превышающих некоторое предельное значение (SS0) (ПДНС)
Т.е. при напряжениях меньше τ0 (ПДНС) данная жидкость обладает свойствами твердого тела, способного только к пластическим (необратимым) деформациям.
где:
Модель Бингама-Шведова
SS – напряжение сдвига;
SS0 – динамическое напрядение сдвига или напряжение сдвига при нулевой скорости сдига;
SR – скорость сдвига;
μпл – пластическая вязкость.

Бингамовская модель вязкопластичной жидкости
Модель Бингама хорошо описывает реологические свойства буровых растворов на водной основе с достаточно высоким содержанием бентонита.
Для расчета параметров модели Бингама по показаниям вискозиметра Фанна используют формулу:
где:
YP и PV – основные реологичесике параметры модели Бингама
Θ – показание вискозиметра;
YP – динамическое напряжение сдвига (фунт/100фут2);
PV – пластическая вязкость (мПа*с или сП);
ω – частота вращения ротора (об/мин).

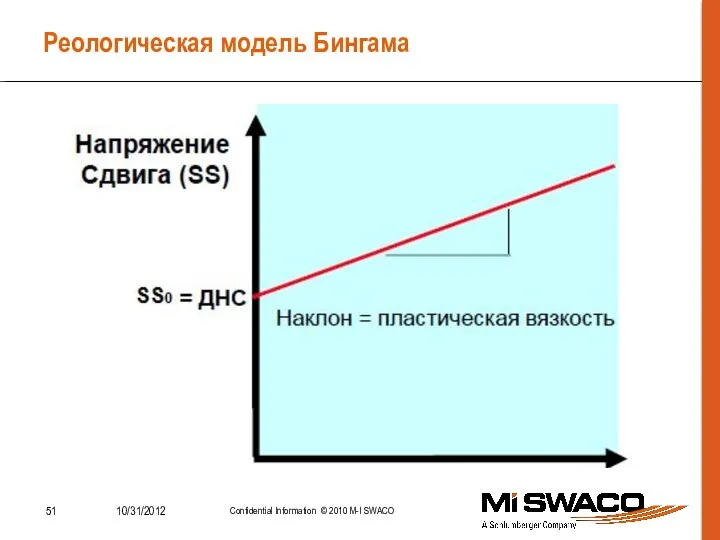
Реологическая модель Бингама

Пластическая вязкость
Пластическая вязкость бурового раствора есть мера механического трения в жидкой фазе раствора диспергированных частиц твердой фазы, эмульгированной фазы, а также макромолекул полимеров.
В соответствии с данным определением на нее влияют:
PV – от англ. Plastic viscosity
концентрация твёрдой фазы;
размер и форма твёрдой фазы;
вязкость жидкой фазы;
присутствие полимеров с линейным строением макромолекул и достаточно длинной молекулярной цепью (POLY-PLUS, HEC (гидроксиэтилцеллюлоза), POLYPAC R, CMC (карбоксиметилцеллюлоза));
соотношение углеводородная фаза/вода (O/W) или синтетическая основа/вода (S/W) в инвертно-эмульсионных растворах;
тип эмульгаторов в инвертно-эмульсионных растворах.

Пластическая вязкость
Росте процентного содержания твердой фазы
Измельчении частиц твердой фазы (при неизменном процентном содержании твердой фазы)
При утяжелении раствора утяжелителем;
Минерализованные буровые растворы имеют более высокую PV, чем растворы на основе пресной воды.
Пластическая вязкость увеличивается при:

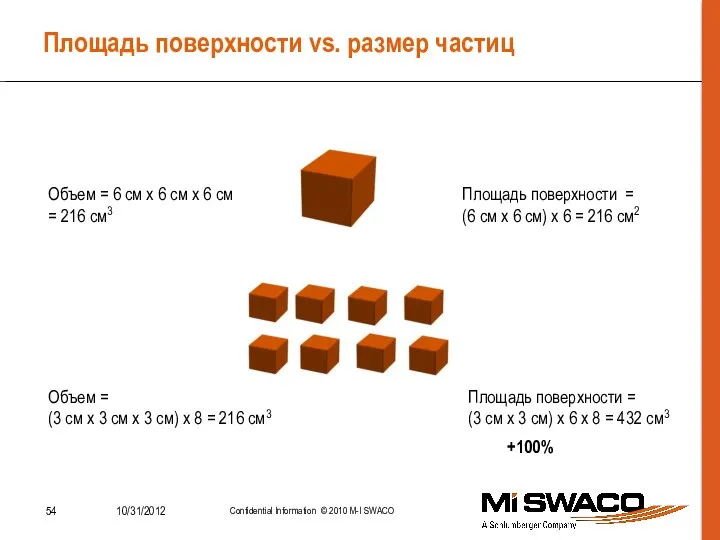
Площадь поверхности vs. размер частиц
Объем = 6 см х 6 см х 6 см = 216 см3
Площадь поверхности =
(6 см х 6 см) х 6 = 216 см2
Объем =
(3 см х 3 см х 3 см) х 8 = 216 см3
Площадь поверхности =
(3 см х 3 см) х 6 х 8 = 432 см3
+100%

Пластическая вязкость
Как правило, PV раствора всегда поддерживается на как можно более низком уровне, так как при уменьшении PV :
долото обеспечивается большей гидродинамической энергией;
эффективность очистки ствола скважины от выбуренной породы возрастает;
уменьшается износ оборудования и экономится горючее.
Снизить PV можно, обусловленную высоким содержанием выбуренной породы можно:
Механической очисткой раствора;
Отстаиванием;
Разбавлением или замещением загрязненного шламом раствора (части или всего его объема) вновь приготовленным.

Динамическое напряжение сдвига
Величина ДНС определяется силой электрохимического взаимодействия между частицами активной твердой фазы (глины), полимеров, дисперсантов.
ДНС зависит от:
Концентрации зарядов на поверхности / сколах частиц твердой фазы;
Объемной концентрации твердой фазы;
Концентрации и типов ионов в жидкой фазе.
YP – от англ. Yield point

Динамическое напряжение сдвига
Заряженные частицы раствора, притягиваясь друг к другу разноименными зарядами, образуют внутреннюю структуру раствора, для разрушения которой требуется приложение дополнительной силы.
В статике прочной этой структуры возрастает со временем (Gels или СНС).
При течении раствора устанавливается динамическое равновесие между количеством вновь образуемых связей частиц и количеством разрушенных при свиге связей.
В соответвии с этим ДНС – мера прочности внутренней структуры раствора в динамических условиях.

Динамическое напряжение сдвига
с ростом концентрации и площади поверхности частиц глины;
загрязнении бурового раствора галитом, ангидритом, гипсом, цементом, сероводородом, углекислотой;
вводе барита (увеличение объемной концентрации твердой фазы в растворе => сокращение расстояния между частицами и увеличение сил притяжения между ними);
переобработках раствора карбонатом и бикарбонатом натрия;
обработках и переобработкх раствора биополимерами (Duo-Vis, Flo-Vis).
YP увеличивается при:

Динамическое напряжение сдвига
при обработках раствора разжижителями-дефлокулянтами (лигнитами, фосфатами, лигносульфонатами);
химической нейтрализации загрязнителей;
при разбавлении раствора водой;
при удалении твердой фазы.
YP уменьшается при:

Упражнение №2
Модель Бингама
Задача:
Площадь верхней пластины = 20 см2
Расстояние между пластинами = 1 см
Минимальная сила, необходимая для сдвига верхней пластины, равна 200 дин.
Сила, необходимая для сдвига верхней пластины со скоростью 10 см/с – 400 дин.
Рассчитайте пластическую вязкость (сП) и ДНС (фунт/100фут2).

Упражнение №2
Решение
При минимальной силе ДНС равна напряжению сдвига при скорости сдвига, равной = 0

Упражнение №2
Продолжение решения
Для того, чтобы двигать пластину со скоростью 10 см/с необходима сила в 400 дин:
Для модели Бингама:
Откуда:

Модель Бингама
Параметры реологической модели Бингама
Уклон
Пластическая вязкость]=[cP]
Отрезок
[ДНС]=[фунт/100фут2]

Кажущаяся вязкость
Кажущейся вязкостью бурового раствора называют его эффективную вязкость при максимальной скорости сдвига 1022 с-1, реализуемой в вискозиметре Фанна.
Рассчитывается по формуле:
AV – от англ. Apparent viscosity
[Кажущаяся взякость] = сП (1 мПа*с)
1 сП = 1 мПа*с

Упражнение №3
Реологические параметры
Задача:
Даны следующие показания вискозиметра VG:
Рассчитайте пластическую вязкость, ДНС и Кажущуюся вязкость.

Ограничения модели Бингама

Ограничения модели Бингама
В широком диапазоне скоростей сдвига модель Бингама достаточно точно описывает соотношение напряжения и скорости сдвига в глинистых растворах низкой плотности.
В большинстве же случаев буровые растворы (особенно содержащие полимеры с большой молекулярной массой) не могут быть точно описаны бингамовской моделью в широком диапазоне скоростей сдвига.

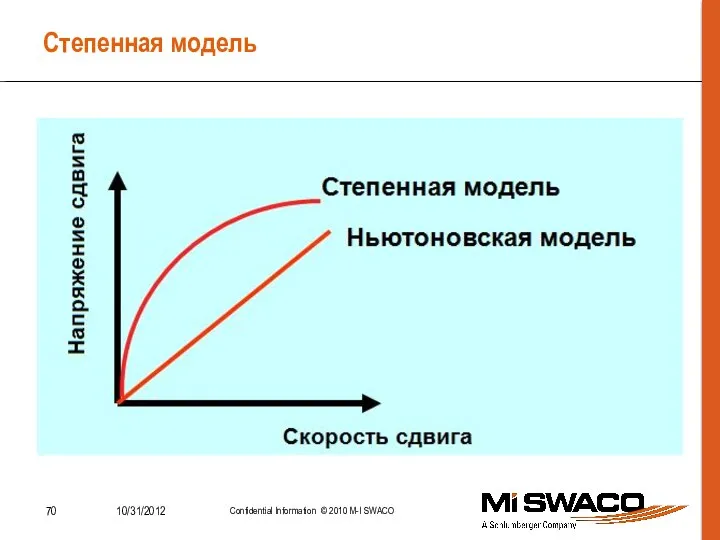
Степенной реологический закон
Степенной реологический закон (для сокращения – Степенной закон) успешно применяется для симуляции поведения буровых растворов на полимерной основе, не имеющих ДНС (например, вязкие чистые соляные растворы).
Применительно к буровым растворам Степенной закон позволяет несколько лучше, чем модель Бингама, описать поведение растворов, прежде всего при малых скоростях сдвига, т.е. в области максимальной нелинейности реологических кривых буровых растворов.
Модель Оствальда - де Ваали

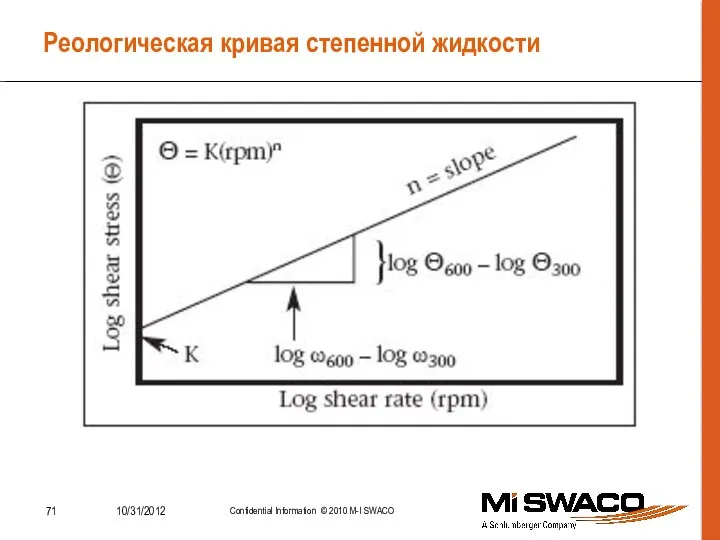
Степенной закон (Power Law)
где:
Математически Степенной закон выражается так:
SS – напряжение сдвига;
K – коэффициент консистенции;
SR - скорость сдвига;
n - показатель степенной зависимости (показатель нелинейности).

Степенная модель

Реологическая кривая степенной жидкости

Степенной закон (Power Law)
Напрямую определяет зависимость вязкости жидкости от скорости сдвига
Очистка скважины и удержание частицы во взвешенном состоянии напрямую зависят от увеличения значения показателя K
В тоже время увеличение показателя К ведет к загущению раствора от выбуренной породы или от переобработки его полимерной химией.
Коэффициент консистентности «K»

Степенной закон (Power Law)
Увеличивается с ростом концентрации твердой фазы и полимеров-загустителей.
Снижается при удалении из раствора твердой фазы, разбавлении водой, обработках раствора дефлокулянтами (лигнитами, фосфатами, лигносульфонатами).
Коэффициент консистентности «K»

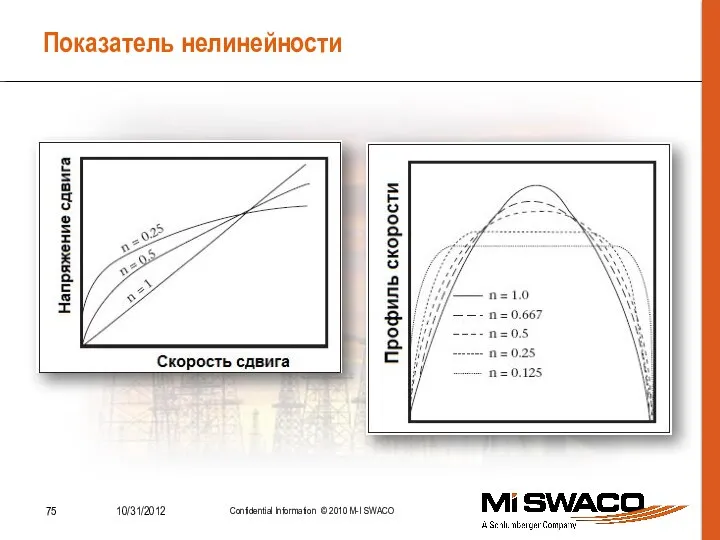
Степенной закон (Power Law)
Определяет степень отличия жидкости от Ньютоновской
Ниже показатель n = менее диспергированный раствор, больше флокулирован и больше отличается от Ньютоновской жидкости
Более низкий показатель n = позволяет увеличивать скорость промывки в кольцевом пространстве и, как следствие, улучшать очистку скважины от ТФ
Показатель нелинейности «n»

Показатель нелинейности

Степенной закон (Power Law)
Показатель нелинейности «n»
n < 1 – жидкость разжижается при сдвиге (пластичная и псевдопластичная жидкость)
n = 1 – ньютоновская жидкость
n > 1 – дилатантная жидкость AV растет с увеличением скорости сдвига

Показатель нелинейности «n»
при увеличении концентрации ксантановых полимеров Duo-Vis, Flo-Vis, XCD, XB
при добавлении солей NaCl, KCl к полимерным растворам
при добавлении прегидратированного бентонита к соленасыщенным и минерализованным буровым растворам
Увеличивается, но не больше, чем 1 (приближение к Ньютоновской модели):
при уменьшении концентрации активной твердой фазы (глины) в пресных растворах,
при вводе крахмала, КМЦ, ПАЦ, полиакрилатов
Уменьшается (приближение к Бингамовской модели):

Упражнение №4
Степенная модель
Задача:
Площадь верхней пластины = 20 см2
Расстояние между пластинами = 1 см
Сила , необходимая для движения пластины со скоростью = 4 см/с, равна 50 дин
Сила, необходимая для движения пластины со скоростью = 10 см/с, равна 100 дин
Вычислите показатель нелинейности n и индекс консистентности K

Упражнение №4
Решение
Уравнение стенного закона:
Сила, необходимая для движения пластины со скоростью 4 см/с:
Уравнение №1

Упражнение №4
Продолжение решения
Сила, необходимая для движения пластины со скоростью 10 см/с:
Уравнение №2

Упражнение №4
Продолжение решения
n Может быть найден из системы уравнений 1 и 2 с помощью логарифмирования:

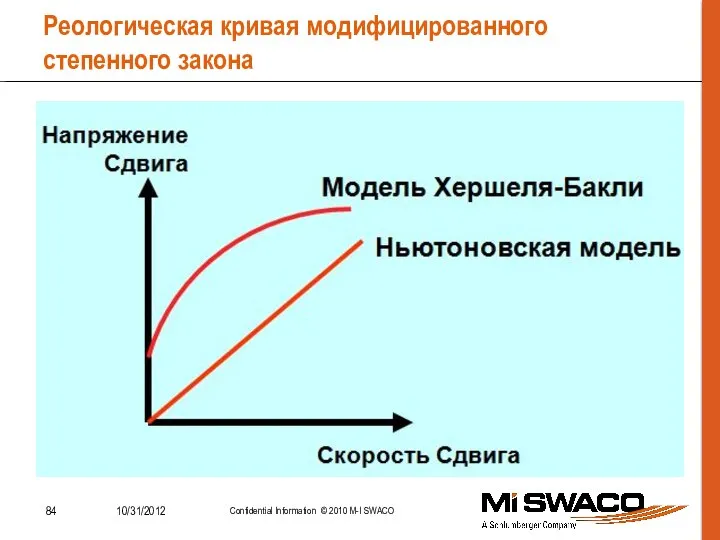
Модифицированный степенной закон
Степенной закон не в полной мере описывает реологические свойства буровых растворов, так как не предсказывает существование для буровых растворов предела текучести.
Степенную модель не сложно модифицировать таким образом, чтобы осправить этот недостаток и использовать полученную модель для вычисления напряжения, требуемого для инициирования движения бурового раствора (Yield stress)
Модель Гершеля-Бакли

Модифицированный степенной закон
где:
Математически модифицированный степенной закон выражается так:
SS – напряжение сдвига;
SS0 – предел текучести (Yield stress);
K – коэффициент консистенции;
SR - скорость сдвига;
n - показатель степенной зависимости (показатель нелинейности).
Данная модель учитывает наличие предельного напряжения сдвига для начала течения жидкости, которое характерно для большинства растворов. Считается, что эта модель наиболее точно передает поведение большинства буровых растворов.

Реологическая кривая модифицированного степенного закона

Модифицированный степенной закон
Напряжение сдвига при нулевой скорости сдвига можно взять из значения параметра LSRYP (Low Share Rate Yield Point) = «Напряжение при низких скоростях сдвига»
Напряжение при низких скоростях сдвига. Это мера вязкости при низкой скорости сдвига. Оно определяет способность раствора к транспортировке шлама в затрубном пространстве. Чем больше частицы шлама, тем выше необходимое значение LSRYP. Оно рассчитывается по формуле:
Напряжение сдвига при низких скоростях сдвига
Как правило значение LSRYP приблизительно равно диаметру ствола в дюймах.
[фунт/100фут2]

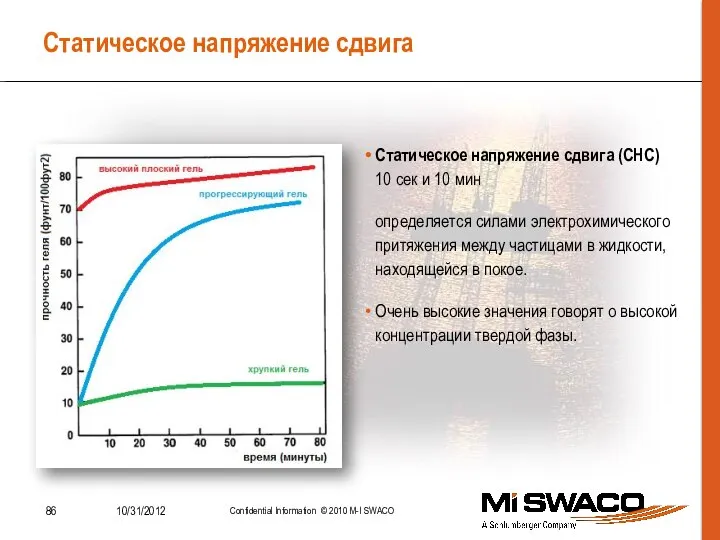
Статическое напряжение сдвига
Статическое напряжение сдвига (СНС) 10 сек и 10 мин
определяется силами электрохимического притяжения между частицами в жидкости, находящейся в покое.
Очень высокие значения говорят о высокой концентрации твердой фазы.

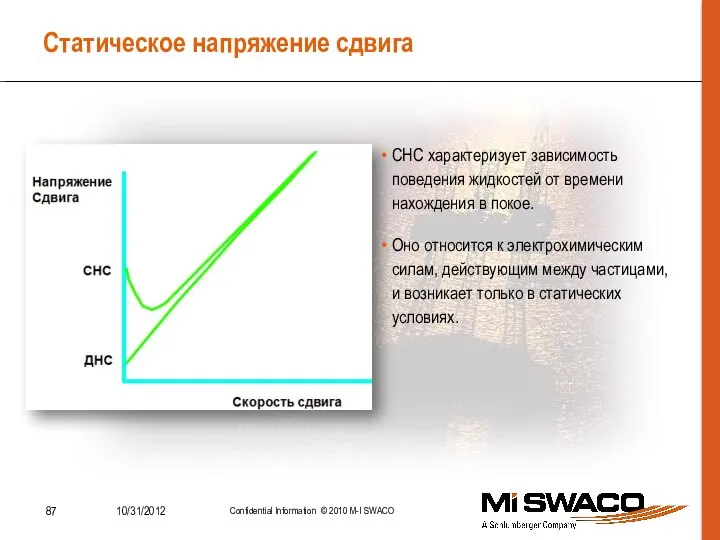
Статическое напряжение сдвига
СНС характеризует зависимость поведения жидкостей от времени нахождения в покое.
Оно относится к электрохимическим силам, действующим между частицами, и возникает только в статических условиях.

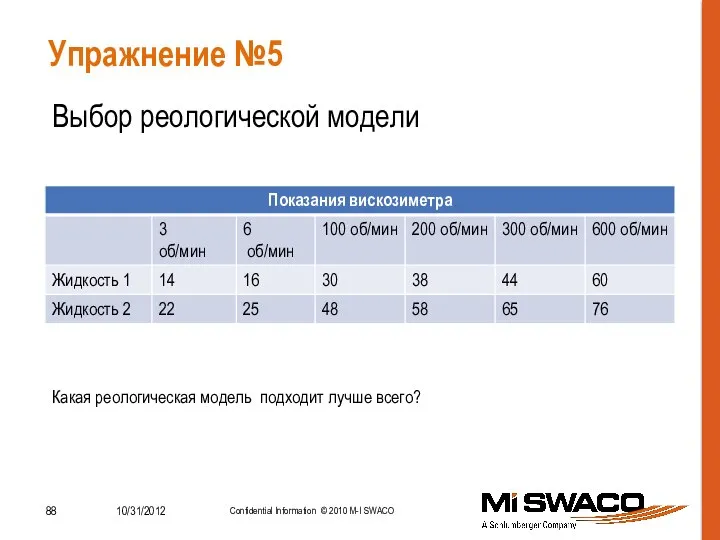
Упражнение №5
Выбор реологической модели
Какая реологическая модель подходит лучше всего?

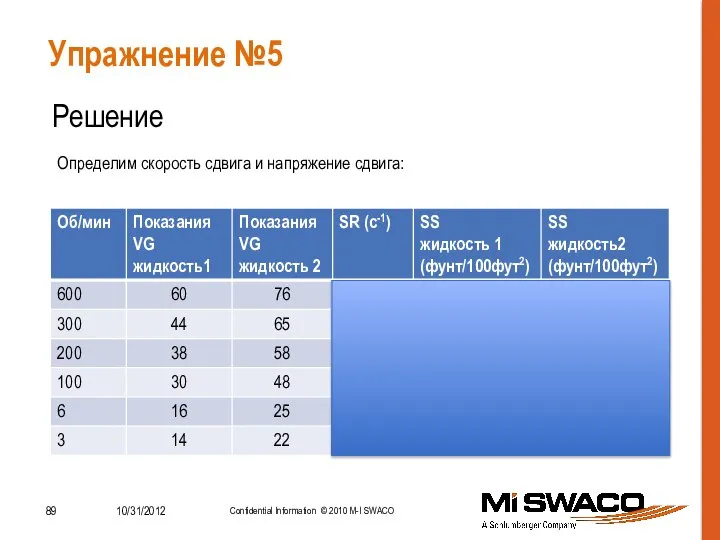
Упражнение №5
Решение
Определим скорость сдвига и напряжение сдвига:

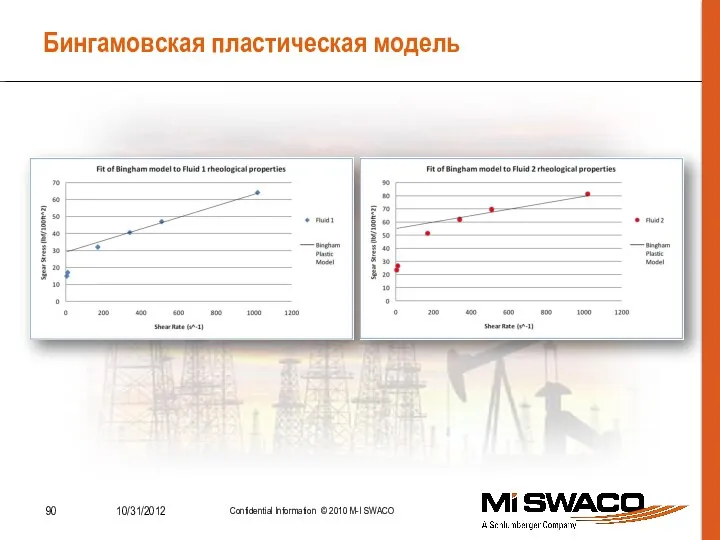
Бингамовская пластическая модель

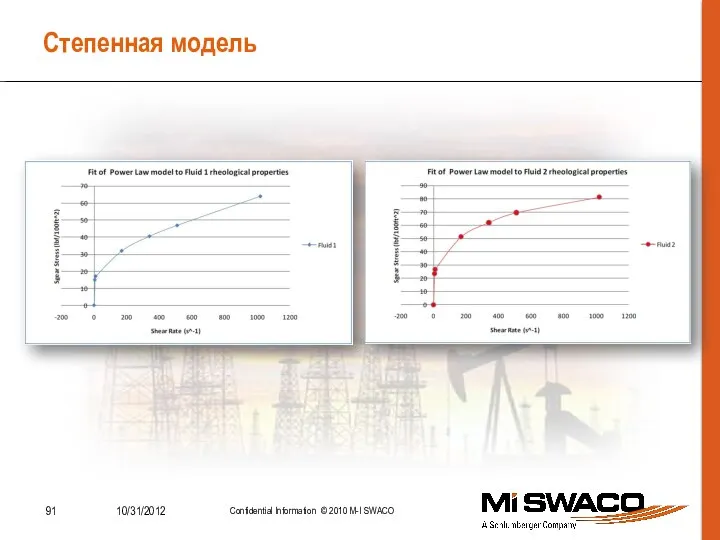
Степенная модель

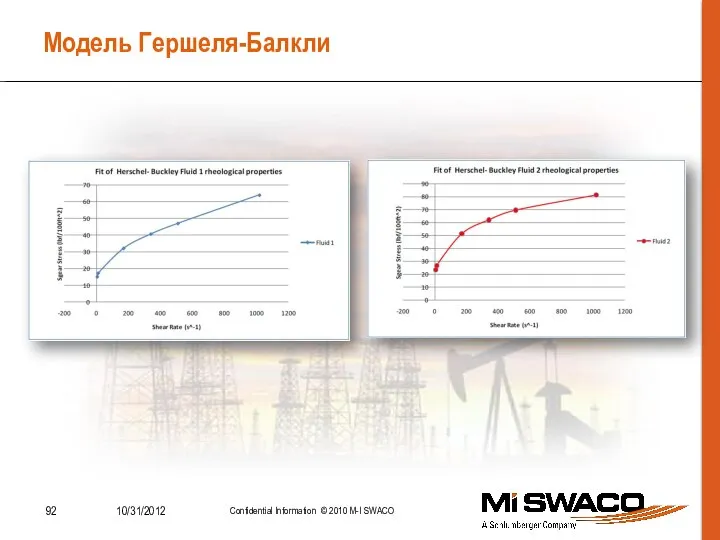
Модель Гершеля-Балкли

Реология и гидродинамика
Режимы течения
Реологические модели
Ньютоновская модель
Бингамовская модель
Степенная модель
Модифицированная степенная модель
Гидродинамические расчеты
Оптимизация гидравлики долота
Программа

Гидродинамические расчеты
Средняя скорость потока в бурильной трубе
Средняя скорость потока в кольцевом пространстве
Средняя скорость потока
где:
V- скорость потока, фунт/мин;
Q – расход бурового раствора (подача насоса), галлон/мин;
D – внутренний диаметр бурильных труб или УБТ, дюйм;
D1 – наружный диаметр бурильных труб или УБТ, дюйм;
D2 – внутренний диаметр обсадной колонны или открытого ствола, дюйм.

Гидродинамические расчеты
Число Рейнольдса для течения раствора в трубах
Число Рейнольдса для течения раствора в кольцевом пространстве
Число Рейнольдса
где:
Ρ – плотность бурового раствора, фунт/галлон;
μep – эффективная вязкость раствора в бурильной колонне, сП (мПа*с);
μea – эффективная вязкость раствора в кольцевом пространстве, сП (мПа*с);

Критическая скорость потока в бурильной колонне
Критический расход бурового раствора в бурильной трубе
Критическая скорость потока в кольцевом пространстве
Критический расход бурового раствора в кольцевом пространстве
Критическая скорость: ламинарный ← V < Vc < V → турбулентный
где:
Kp и Ka – коэффициент консистенции раствора для труб и кольцевого пространства, дн*сn/см2 (дПа*сn);
np и na – показатель нелинейности раствора для труб и кольцевого пространства, дн*сn/см2 (дПа*сn).

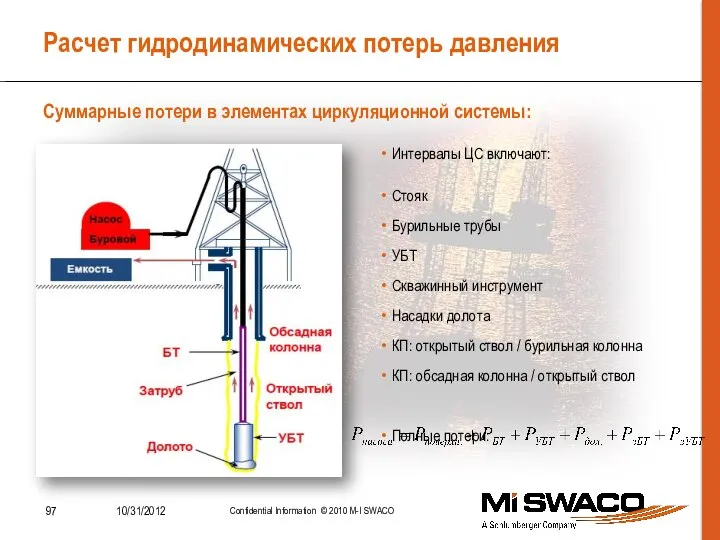
Расчет гидродинамических потерь давления
Суммарные потери в элементах циркуляционной системы:
Интервалы ЦС включают:
Стояк
Бурильные трубы
УБТ
Скважинный инструмент
Насадки долота
КП: открытый ствол / бурильная колонна
КП: обсадная колонна / открытый ствол
Полные потери:

Расчет гидродинамических потерь давления
Коэффициент гидравлического сопротивления труб
При Re≤2100 При Re≥2100
Потери давления в бурильной колонне:
Потери давления в бурильной колонне
где:
Ρр – потери давления, фунт/дюйм2;
Vp – средняя скорость потока, фунт/мин;
ρ – плотность раствора, фунт/галлон;
L – длина интервала, фут.

Расчет гидродинамических потерь давления
Коэффициент гидравлического сопротивления кольцевого пространства
При Re≤2100 При Re≥2100
Потери давления в интервале кольцевого пространства:
Потери давления в кольцевом пространстве
где:
Ρa – потери давления, фунт/дюйм2;
Va – средняя скорость потока, фунт/мин;
ρ – плотность раствора, фунт/галлон;
L – длина интервала, фут;
D1 – наружный диаметр бурильных труб или УБТ, дюйм;
D2 – внутренний диаметр скважины или обсадной колонны, дюйм.

Расчет гидродинамических потерь давления
Потери давления на долоте в пересчете на размер насадок долота рассчитываются по формуле:
Потери давления на долоте (в насадках долота)
где:
Ρbit – потери давления, фунт/дюйм2;
ρ – плотность раствора, фунт/галлон;
Dн –внутренний диаметр насадки №1, №2, №3…. в 1/32 дюйма.
Для расчета потери давления в колонковых долотах или алмазных долотах в расчетную формулу следует подставлять суммарную площадь поперечного сечения / Total Flow Area:
где: TFA – суммарнаяя площадь поперечного сечения, дюйм2

Расчет гидродинамического режима работы долота
Так как на долоте возможна установка насадок различного диаметра, рассчитывается усредненное значение скорости истечения раствора из насадок долота по формуле:
Скорость истечения из насадок долота
где:
Q – расход, галлон/мин;
Dн – внутренний диаметр насадки №1, №2, №3… в 1/32 дюйма.
Для большинства долот рекомендуются скорости истечения в диапазоне от 250 до 450 фут/с. Скорости истечения, превышающие 450 фут/с, могут привести к эрозии режущей части долота.

Расчет гидродинамического режима работы долота
Как правило, желательно, чтобы потери давления на долоте составляли 50-65% давления нагнетания раствора.
Потери давления в процентном выражении

Для расчета давления, которое циркулирующий буровой раствор оказывает на пласт, необходимо к гидростатическому давлению бурового раствора на данной глубине прибавить потери давления циркуляции в кольцевом пространстве в интервале от интересующей нас глубины скважины до устья скважины.
ECD бурового раствора на заданной глубине равна плотности бурового раствора, который в отсутствии циркуляции создает на данной глубине такое же давление.
Эквивалентная циркуляционная плотность - ECD
где:
TVD – глубина по вертикали / True Vertical Depth, фут.

Оптимизация гидравлики на долоте
Однако, помимо гидравлики существует множество других факторов, влияющих на скорость проходки:
Размер / тип / характеристики долота
Тип и твердость пород и т.д.
Цель оптимизации гидравлики на долоте – увеличение МСП
Задачей оптимизации гидравлики является достижение баланса между давлением внутри скважины, расходом раствора, очисткой ствола, давлением на насосе, ЭЦП и потерей давления на долоте при максимальном увеличении скорости проходки
На практике, оптимизация гидравлики означает поиск наилучшего сочетания расхода раствора и размера насадок для данной глубины.

Оптимизация гидравлики на долоте
Метод максимума гидравлической мощности на долоте / Bit Hydraulic Horsepower (HHP)
Метод максимума ударной силы струи / Jet Impact Force (JIF)
Существует два критерия оптимизации гидравлики на долоте:
Каждый критерий дает разное значение потери давления на долоте, разные размеры насадок и оптимальные расходы раствора.
Мы подробно рассмотрим оба критерия и представим краткий метод оптимизации гидравлики долота.

Расчет гидродинамического режима работы долота
Гидравлическая мощность на долоте рассчитывается по формуле:
Гидравлическая мощность на долоте
где:
Q – расход, галлон/мин;
Pbit – потери давления на долоте, фунт/дюйм2.
Гидравлическая мощность на квадратный дюйм площади долота:
Рекомендуемый диапазон значений hhpb (hydraulic horse power at a bit) для большинства долот равен 2,5-5,0 лошадиных сил на квадратный дюйм площади долота.
Низкая гидравлическая мощность на долоте может привести к низкой скорости проходки и нерациональной эксплуатации долота.

Расчет гидродинамического режима работы долота
Гидравлическая мощность на долоте не может превышать гидравлическую мощность всей циркуляционной системы (насоса), рассчитываемую по формуле:
Гидравлическая мощность циркуляционной системы
где:
Ptotal – полные потери давления в циркуляционной системе (давление на стояке), фунт/дюйм2;
Q – расход, галлон/мин.

Расчет гидродинамического режима работы долота
Сила, оказывающая давление жидкостью, выходящей под долотом: вся кинетическая энергия жидкости, состоящая из массы и скорости, разрушается при ударе о забой ствола.
Сила гидроудара
Где:
JIF – сила гидроудара / Jet Impact Force/, фунт;
Vн – скорость истечения из насадок, фут/с;
Q – расход, галлон/мин;
ρ – плотность раствора, фунт/галлон.

Расчет гидродинамического режима работы долота
Рассчитывается по формуле:
Сила гидроудара на квадратный дюйм долота

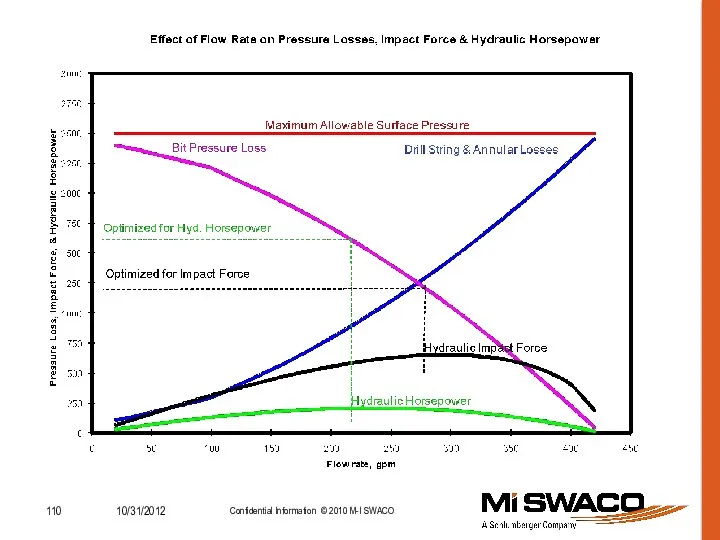
Рекомендации по гидравлике долота
Максимизировать гидравлическую мощность в л.с. на кв. дюйм площади долота (HSI) с скорость струи для твердых пород или при прилипании пород на долото
При бурении твердых пород ограничивать скорость бурения будут скопления обломков породы и мелкой крошки под долотом. Большое значение здесь имеет размывающее породу действие струй бурового раствора – гидромониторный эффект
Скорость бурения может быть увеличена за счет оптимизации величины гидравлической мощности
Максимальная гидравлическая мощность

Рекомендации по гидравлике долота
Максимизировать ударную силу струи в мягких породах, в которых потенциальным ограничением является налипание породы на долото, образование сальников, очистка ствола скважины от выбуренной породы
Максимальная сила ударной струи
Распространено в верхних секциях с высокой скоростью проходки и химически активными пластами
Но следует помнить о потребностях наклонно-направленного бурения в мягких породах. Высокая ударная сила может снизить скорость набора кривизны (из-за размыва ствола перед долотом)