РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ

Цели урока
развитие внимания, мышления;
изучение нового приёма решения квадратных уравнений по формуле;
привитие аккуратности в работе.
повторение изученного материала;

Задачи урока
2. Развивать навыки самостоятельной работы.
1. Вывести формулы корней квадратного уравнения и закрепить изученный материал решениями примеров.
3. Вырабатывать умение слушать
ответы учителя и учащихся.

Повторение
Что такое квадратное уравнение?
Уравнение вида
где a,b,c – заданные числа, а ≠ 0, х – неизвестное (независимая переменная) называется квадратным.
Является ли квадратным уравнение:
а)
б)
Как называются коэффициенты a, b, c ?

Повторение
Какие бывают квадратные уравнения?
Уравнения вида
где a,b,c – некоторые числа, отличные от нуля -
называются неполными квадратными
уравнениями.
Как решается уравнение где d > 0 ?

Решение задач

Решение задач

Решение задач

Изучение нового материала
Из истории квадратных уравнений (сообщение).
Неполные квадратные уравнения и частные виды полных квадратных уравнений умели решать вавилоняне (примерно за 2 тысячи лет до новой эры). Некоторые виды квадратных уравнений решали древнегреческие математики, сводя их решение к геометрическим построениям. Правило решения квадратных уравнений, приведённых к виду
где а > 0, дал индийский учёный Брахмагупта (VII в.). Вывод формулы корней квадратного уравнения в общем виде имеется у Виетта, однако он признавал только положительные корни. Итальянские математики XVI в. учитывают помимо положительных и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других учёных способ решения квадратных уравнений принимает современный вид.

Вывод формулы нахождения корней квадратного уравнения
Познакомимся с ещё одним способом решения, который позволит быстро находить корни квадратного уравнения.
Попробуем это сделать в процессе выполнения
математического диктанта.
Будьте предельно внимательны,
старайтесь сделать всё сами!!!

Диктант
1. Умножим обе части уравнения
на 4а;
2. Перенесём свободный член вправо:
3. Дополним левую часть уравнения до полного квадрата, для чего к обеим частям уравнения прибавим по
следовательно,

Диктант
Так как то, используя известную
теорему,
имеем: откуда
Мы получили формулу для вычисления корней квадратного уравнения. Сколько всего корней ?
Введём обозначение это число – дискриминант квадратного уравнения. Тогда формула корней принимает вид:
где b, a – коэффициенты квадратного уравнения.

Диктант
если D > 0, то уравнение имеет два корня; если D = 0, то уравнение имеет одно решение;
если D < 0, то уравнение не имеет корней.
Пример. Решите уравнение
Следовательно, уравнение имеет два различных корня, найдём их:
Итак,

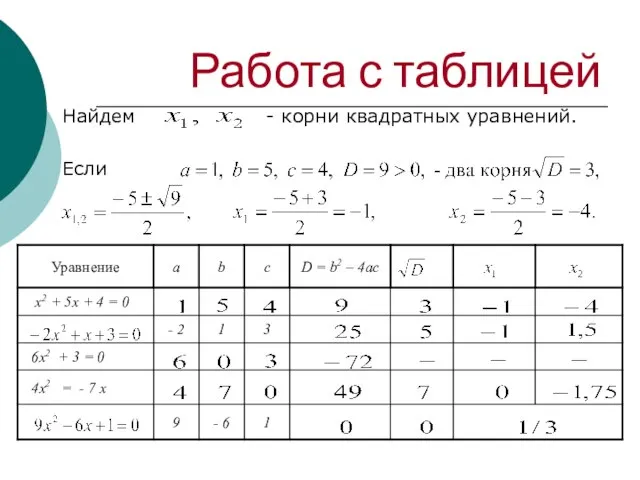
Работа с таблицей
Найдем - корни квадратных уравнений.
Если

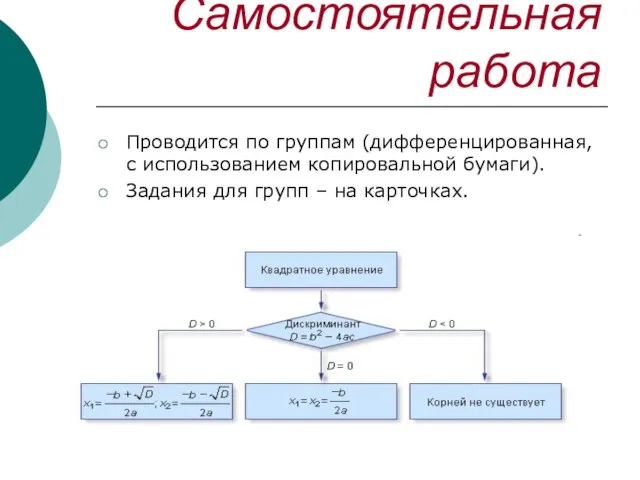
Самостоятельная работа
Проводится по группам (дифференцированная, с использованием копировальной бумаги).
Задания для групп – на карточках.

Самостоятельная работа
1 группа
а) Решите уравнение
Решение:
Ответ:
б) Дополнительное задание:
Решение:
Ответ:

Самостоятельная работа
2 группа
а) Решите уравнение
Решение:
Ответ:
б) Дополнительное задание:
Решение:
Ответ:

Самостоятельная работа
3 группа
Решить уравнение:
Решение:
Ответ:
б) Дополнительное задание:
Решение:
Ответ:

Запишите корни в порядке возрастания и прочитайте зашифрованное слово

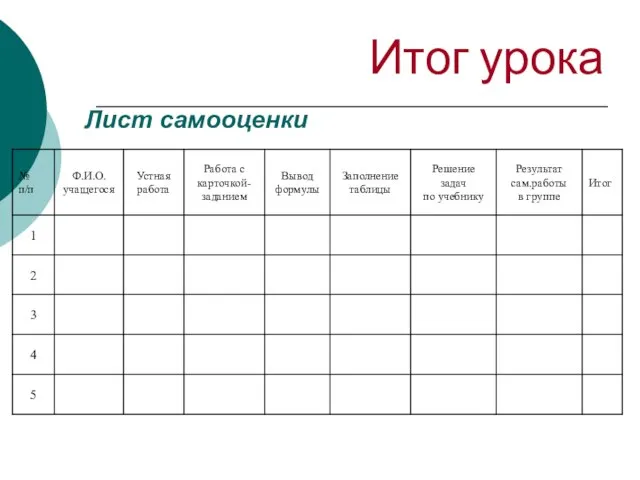
Итог урока
Лист самооценки