Решение логических задач на олимпиадах по обществознанию (методические указания и комментарии к оцениванию)
Содержание
- 2. Содержание Общие требования и критерии Задачи на анализ логической формы Задачи на установление соответствия Задачи с
- 3. 1. Общие требования и критерии
- 4. Какие качества и способности проверяются? Внимательность Умение «держать мысль» Ясность Четкость Последовательность Чувствительность к «граничным условиям»
- 5. Требования При решении логических задач в олимпиадах по обществознанию не требуется знание специальных логических методов и
- 6. Картезианские «правила метода» Правило очевидности Правило анализа Правило последовательности Правило полноты
- 7. Критерии Задача считается решенной полностью только при наличии правильного ответа и исчерпывающего обоснования Всевозможные схемы, таблицы,
- 8. Часто встречающиеся ошибки Неправильно проанализирована логическая форма отрицание / утверждение? и / или? все / некоторые?
- 9. Например Многие депутаты поддержали законопроект (все? некоторые?) Курить и употреблять спиртные напитки запрещено (и? или?) Все
- 10. Часто встречающиеся ошибки Утверждаемое заключение не следует логически из посылок («non sequitur»)
- 11. Часто встречающиеся ошибки Предвосхищение основания («petitio principii») Бог существует, поскольку об этом говорится в Библии, которая,
- 12. Часто встречающиеся ошибки Отступление от тезиса («Ignoratio elenchi») Доказывается не то, что следует, или опровергается не
- 14. 2. Задачи на анализ логической формы
- 15. Проверим внимательность Может ли католик жениться на сестре своей вдовы?
- 16. Проверим внимательность В городе есть всего два парикмахера, у каждого из которых своя парикмахерская Заглянув в
- 17. Задача 1 Директор школы возражает против отмены решения о запрете контроля за прическами Тем самым он
- 18. Решение Свобода причесок (А) Контроль за прическами (не-А) Запрет контроля за прическами (не-не-А) Отмена решения о
- 19. Задача 2 Спикер безапелляционно отверг домыслы о том, что он собирается отменить приказ о запрете уклонения
- 20. Задача 3 Джонс, Смит и Браун подозреваются в преступлении. Виновен только один из них . Джонс
- 21. Решение Утверждения Смита и Брауна противоречат друг другу («Это сделал Браун», «Браун не виновен») Значит, один
- 22. 3. Задачи на установление соответствия
- 23. Задача 4 В одном классе учились три девушки – Лена, Оля и Катя Лена сказала: «Я
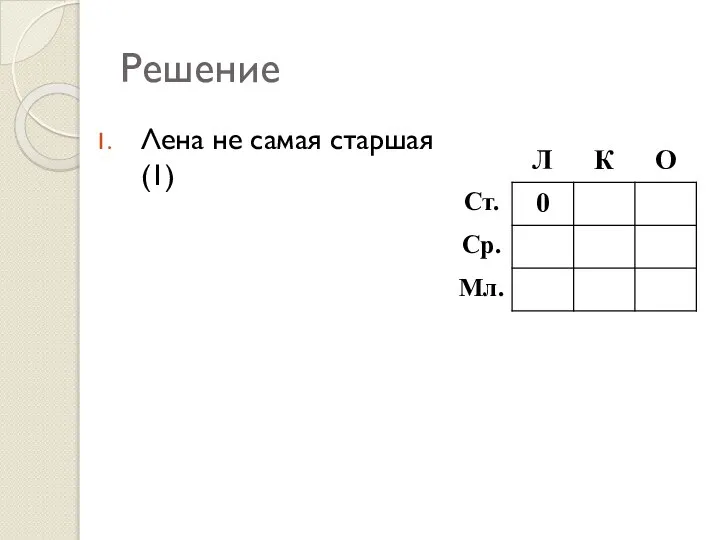
- 24. Решение Лена не самая старшая (1)
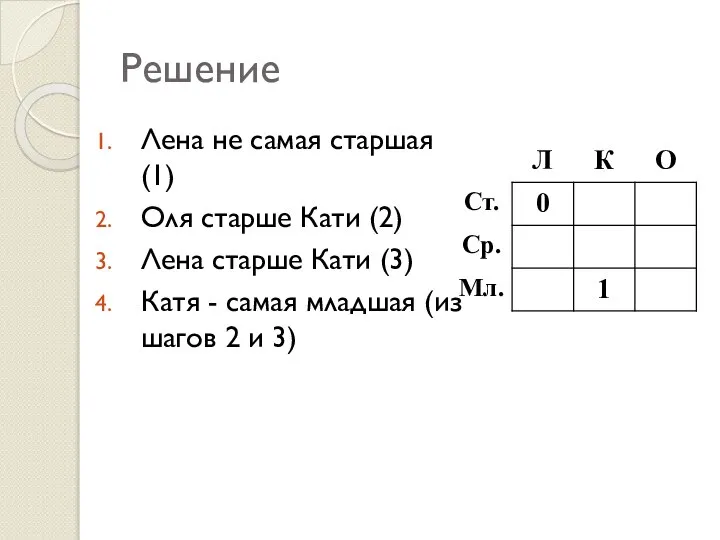
- 25. Решение Лена не самая старшая (1) Оля старше Кати (2) Лена старше Кати (3) Катя -
- 26. Решение Лена не самая старшая (1) Оля старше Кати (2) Лена старше Кати (3) Катя -
- 27. Решение Лена не самая старшая (1) Оля старше Кати (2) Лена старше Кати (3) Катя -
- 28. Решение Лена не самая старшая (1) Оля старше Кати (2) Лена старше Кати (3) Катя -
- 29. Задача 5 В одном классе учатся Андреев, Борисов и Васильев. Один из них отличник, другой хорошист,
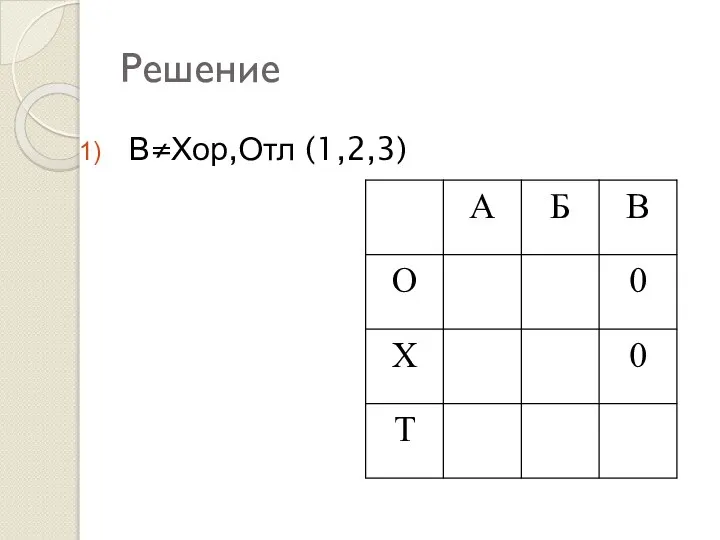
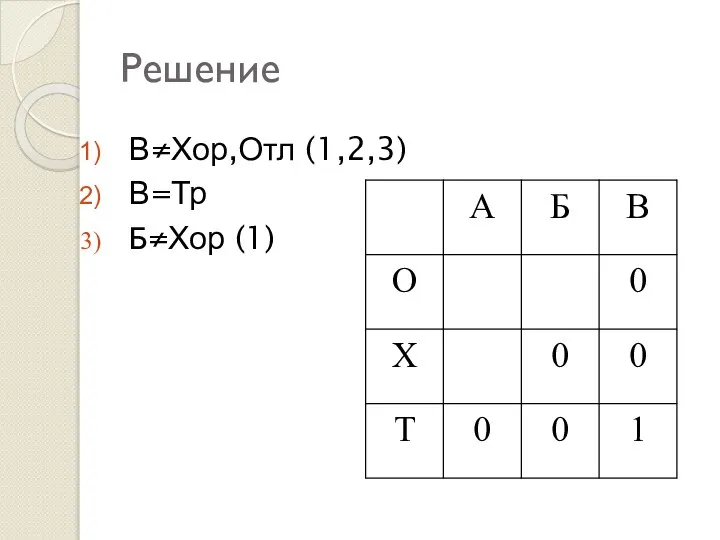
- 30. Решение В≠Хор,Отл (1,2,3)
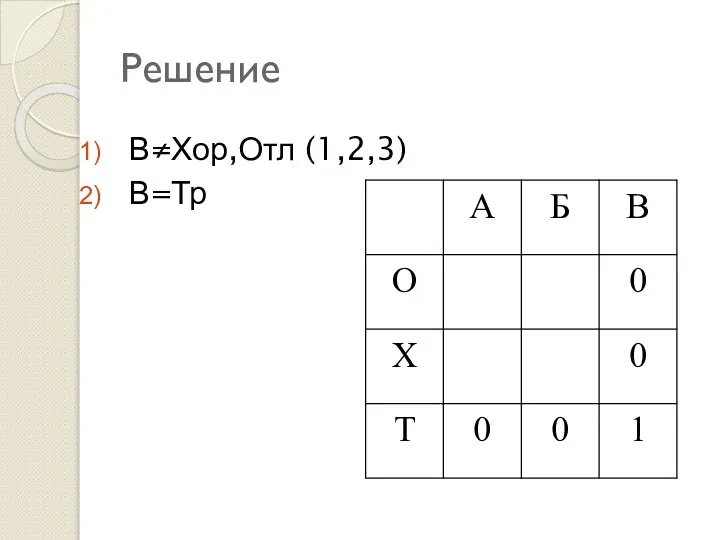
- 31. Решение В≠Хор,Отл (1,2,3) В=Тр
- 32. Решение В≠Хор,Отл (1,2,3) В=Тр Б≠Хор (1)
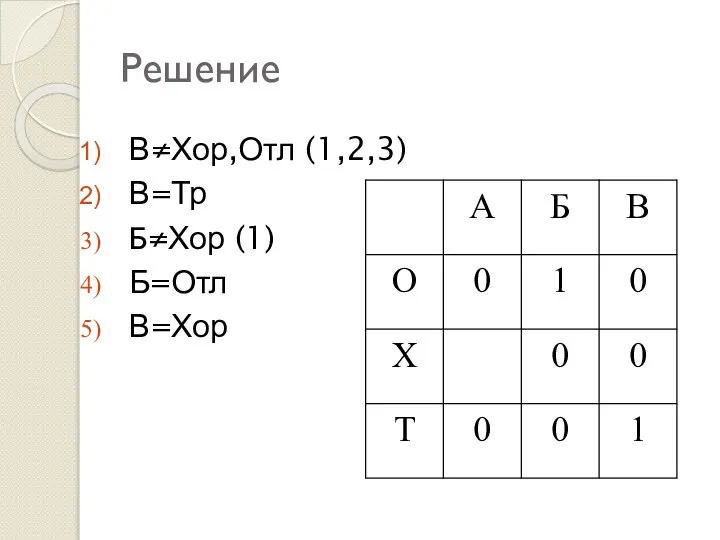
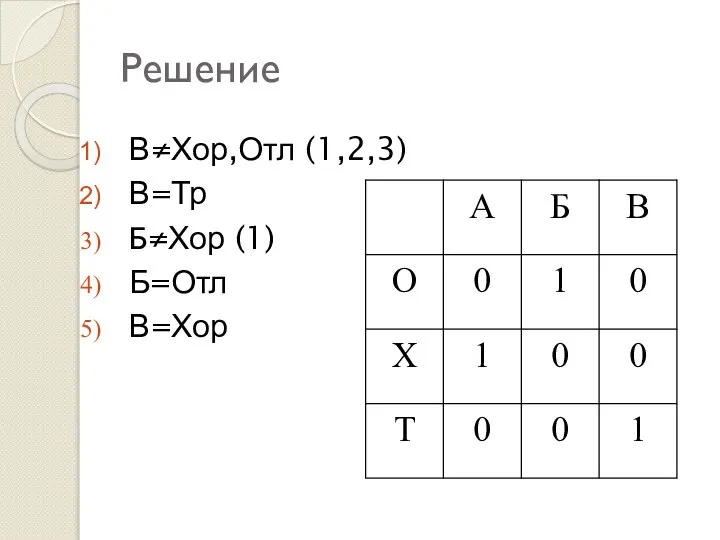
- 33. Решение В≠Хор,Отл (1,2,3) В=Тр Б≠Хор (1) Б=Отл В=Хор
- 34. Решение В≠Хор,Отл (1,2,3) В=Тр Б≠Хор (1) Б=Отл В=Хор
- 35. 4. Задачи с саморекурсивными условиями
- 36. Что такое рекурсия? Реку́рсия — наличие в определении, описании, изображении какого-либо объекта или процесса самого этого
- 37. Задача 6 На одном острове живут два племени Люди племени А всегда говорят правду, а люди
- 38. Решение Что значит ответ «Тарабара?» На вопрос «ты лжец?» любой ответит «Нет» (Ср.: парадокс лжеца) «Тарабара»
- 39. Задача 7
- 40. 1) Все следующие предложения ложны . . . n) Все следующие предложения ложны n+1) Некоторые предыдущие
- 41. Задача 8 В одном храме собрались три божества – бог Истины (всегда говорит правду), бог Лжи
- 42. Решение 1 не бог Истины (такой только один, значит, он не может назвать кого-то другого богом
- 43. 5. Задачи на когнитивное моделирование
- 45. Задача 9 Есть три колпака – два белых и один черный Двое игроков закрывают глаза и
- 46. Сложность в том, что обоим игрокам надели белые колпаки На первый взгляд, при таком раскладе задача
- 47. Решение На моем противнике белый колпак Значит, на мне самом может быть белый или черный Предположим,
- 48. Задача 10 Могущественный некромант заточил в темницу двух белых магов и подверг их суровому испытанию. Суть
- 49. Ответ Каждый из них должен написать число, которое видит на лбу другого.
- 50. Решение Если я вижу у него 0, произведение в любом случае будет равно 0. Значит, надо
- 52. Скачать презентацию










































 Тема ответственностичеловека за свои поступки в произведениях кубанских писателей
Тема ответственностичеловека за свои поступки в произведениях кубанских писателей Повторение сведений об имени существительном, имени прилагательном и глаголе
Повторение сведений об имени существительном, имени прилагательном и глаголе Преобразование выражений, содержащих операцию извлечения квадратного корня
Преобразование выражений, содержащих операцию извлечения квадратного корня 163 Когда тяжесть
163 Когда тяжесть Техника изонити 2 урок
Техника изонити 2 урок «Работа выполнена в рамках проекта «Повышение квалификации различных категорий работников образования и формирование у них базо
«Работа выполнена в рамках проекта «Повышение квалификации различных категорий работников образования и формирование у них базо Николай Михайлович Карамзин
Николай Михайлович Карамзин Мода Японии в эпохе Эдо (1600-1868)
Мода Японии в эпохе Эдо (1600-1868) В гостях у Маши (5 класс)
В гостях у Маши (5 класс) Размножение земноводных
Размножение земноводных Satul de vacanță “ Poiana Rustică”
Satul de vacanță “ Poiana Rustică” Ядовитые растения
Ядовитые растения Партнерская программа для ИНТЕРНЕТ-МАГАЗИНОВ
Партнерская программа для ИНТЕРНЕТ-МАГАЗИНОВ Государственный музей истории космонавтики имени К. Э. Циолковского
Государственный музей истории космонавтики имени К. Э. Циолковского План характеристики отделов водорослей
План характеристики отделов водорослей Религиозная культура Древней Индии. Индуизм
Религиозная культура Древней Индии. Индуизм Стандарты второго поколения
Стандарты второго поколения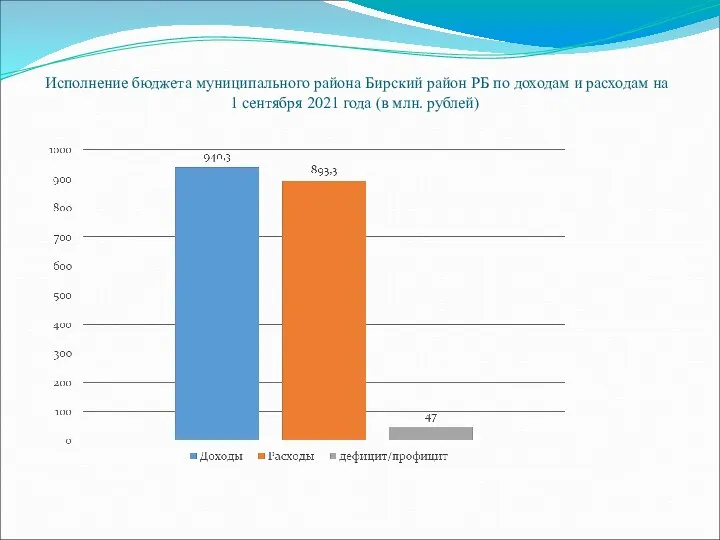 Исполнение бюджета муниципального района Бирский район РБ по доходам и расходам
Исполнение бюджета муниципального района Бирский район РБ по доходам и расходам Weimar Constitution
Weimar Constitution Транспортная компания ТК Нерпа
Транспортная компания ТК Нерпа Кукла в творчестве Д.Д.Шостаковича. Матрешка как разновидность народного творчества
Кукла в творчестве Д.Д.Шостаковича. Матрешка как разновидность народного творчества ОРКСЭ. Почему я выбираю Основы православной культуры
ОРКСЭ. Почему я выбираю Основы православной культуры Презентация на тему Red Bull: вред или польза
Презентация на тему Red Bull: вред или польза «Информатизация и Школа»Григорьева Ольга Владимировназаместитель директорапо Информационным ТехнологиямГОУ СОШ №867
«Информатизация и Школа»Григорьева Ольга Владимировназаместитель директорапо Информационным ТехнологиямГОУ СОШ №867 Сочи – мой любимый город
Сочи – мой любимый город Открытый доступ: механизмы, инструменты и первые результаты принятия Белгородской декларации об открытом доступе к научному знан
Открытый доступ: механизмы, инструменты и первые результаты принятия Белгородской декларации об открытом доступе к научному знан друзья весны
друзья весны Плазменные мониторы в МакДональдз®: восприятие потребителей
Плазменные мониторы в МакДональдз®: восприятие потребителей