Слайд 2Цели:
расширение и углубление представлений учащихся о решении уравнений, организация поисковой деятельности учащихся

при решении неполных квадратных уравнений;
развитие умения самостоятельно приобретать новые знания;
Слайд 3Эпиграфом урока сегодня будут слова Л. Морделла
«Математик иногда испытывает большую радость

от сознания, что давняя проблема уже решена».
Слайд 4Устная работа
Разложите на множители.

Слайд 5Решите уравнения.
Сколько корней имеет каждое уравнение?

Слайд 6Распределите данные уравнения на группы и объясните, по какому признаку вы это

сделали.
Слайд 7Возможные ответы:
1-я группа:
а), д);,
2-я группа:
б), и); оба слагаемых содержат

переменную,
3-я группа:
е), ж); одно слагаемое с переменной, а другое – нет;
4-я группа:
в), з); одночлен с переменной в квадрате).
Слайд 8Постановка учебной задачи.
1. Как называются эти уравнения?
2. Представьте уравнения 1-й группы

в общем виде.
3. Дайте определение этому уравнению.
4. Все ли уравнения здесь полные?
Слайд 10Обучающая самостоятельная работа
Вариант 1 Вариант 2

Слайд 11Составьте квадратное неполное уравнение, имеющее корни:
Вариант 1 Вариант 2
а) 5 и

– 5, а) 6 и 0,
б) – 4 и 0, б) 3 и – 3.
Слайд 12Решите уравнение:
Вариант 1 Вариант 2
1) 1)
2) 2)

Слайд 13Подведение итогов урока.
Решая квадратные уравнения, вы убедились в том, что, зная

различные способы их решения, можно решать эти уравнения быстро, правильно и красиво.
Неполные квадратные уравнения:
1) ax2 + bx = 0;
2) ax2 + c = 0; левую часть удобно представить в виде разности квадратов двух выражений;
3) ax2 + c = 0; левую часть неудобно представить в виде разности квадратов двух выражений.












 Эндокринная Артериальная гипертензия
Эндокринная Артериальная гипертензия Историческая справка Здание нашего детского сада было построено в 19.. году За это время здесь побывали и ясли и центр детского твор
Историческая справка Здание нашего детского сада было построено в 19.. году За это время здесь побывали и ясли и центр детского твор Результаты единого государственного экзамена в 2019 году
Результаты единого государственного экзамена в 2019 году Задачи знатокам
Задачи знатокам Секреты успеха. Процветание - это установка сознания и жизненный принцип
Секреты успеха. Процветание - это установка сознания и жизненный принцип Фольклор в музыке
Фольклор в музыке The United States of America
The United States of America Демонстрационная программа в Центре подготовки космонавтов им. Ю.А. Гагарина
Демонстрационная программа в Центре подготовки космонавтов им. Ю.А. Гагарина Презентация на тему каждый человек может научиться рисовать
Презентация на тему каждый человек может научиться рисовать  Заглавная буква в словах 1 класс
Заглавная буква в словах 1 класс Порядок подачи заявления о преступлении
Порядок подачи заявления о преступлении Топчик
Топчик Великие изобретения человечества
Великие изобретения человечества «Счастливая семья – счастливые дети»
«Счастливая семья – счастливые дети» Антикризисное управление. Основные понятия (1)
Антикризисное управление. Основные понятия (1) Документы и сведения, представляемые таможенным органам при прибытии на таможенную территорию Подготовили: студентки 3-го курса
Документы и сведения, представляемые таможенным органам при прибытии на таможенную территорию Подготовили: студентки 3-го курса  степ функ2
степ функ2 ТЭК. Топливная промышленность России
ТЭК. Топливная промышленность России Изображения детей в картинах художников
Изображения детей в картинах художников Пещерная живопись. Человек и обитатели наших степей
Пещерная живопись. Человек и обитатели наших степей Оптические явления в атмосфере
Оптические явления в атмосфере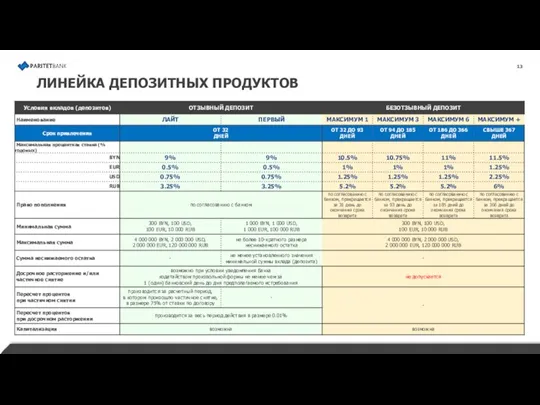 Линейка депозитных продуктов
Линейка депозитных продуктов Презентация Джулай
Презентация Джулай Святитель Иоанн Златоуст
Святитель Иоанн Златоуст Политический кризис 1993
Политический кризис 1993  Деятельность ОУ по обеспечению мониторинговых процедур. КПМО.
Деятельность ОУ по обеспечению мониторинговых процедур. КПМО. Влияние окружающей среды на человека
Влияние окружающей среды на человека Положение об отделе
Положение об отделе