Содержание
- 2. 2. Пересечение геометрических объектов общего положения 2.1. Общий алгоритм способа вспомогательных секущих поверхностей. 2.2. Способ вспомогательных
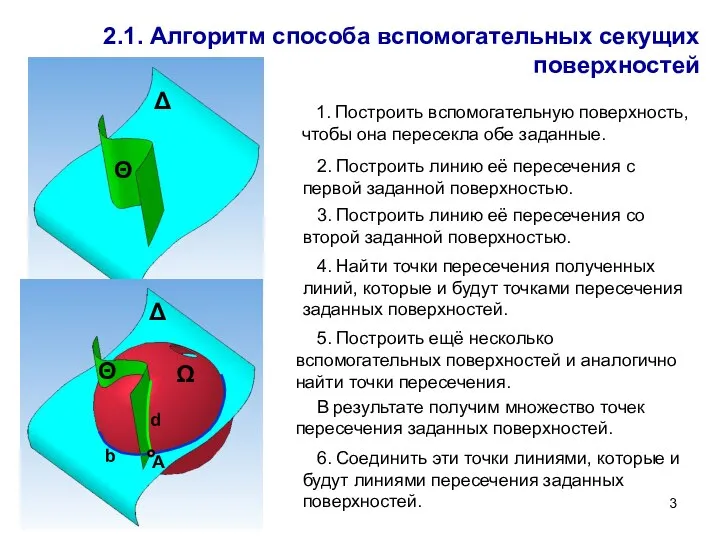
- 3. 2.1. Алгоритм способа вспомогательных секущих поверхностей 1. Построить вспомогательную поверхность, чтобы она пересекла обе заданные. 2.
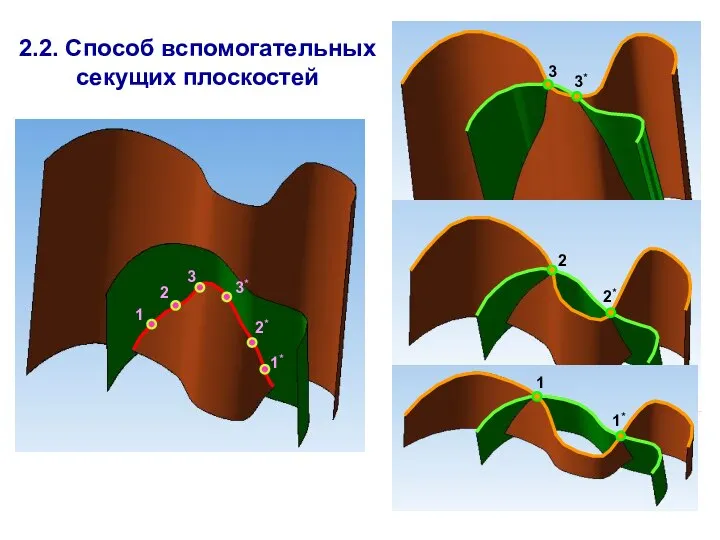
- 4. 2.2. Способ вспомогательных секущих плоскостей 1 2 2* 1* 3* 3 1 2 2* 1* 3*
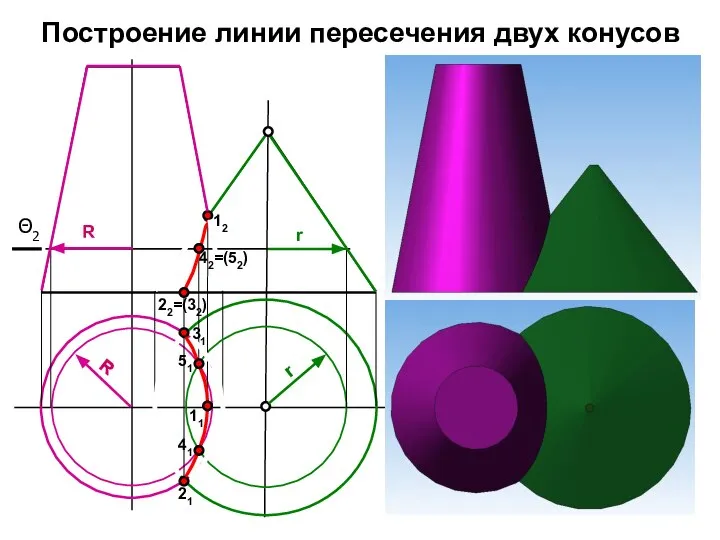
- 5. Построение линии пересечения двух конусов Θ2 12 42=(52) 22=(32) 11 21 31 41 51 R R
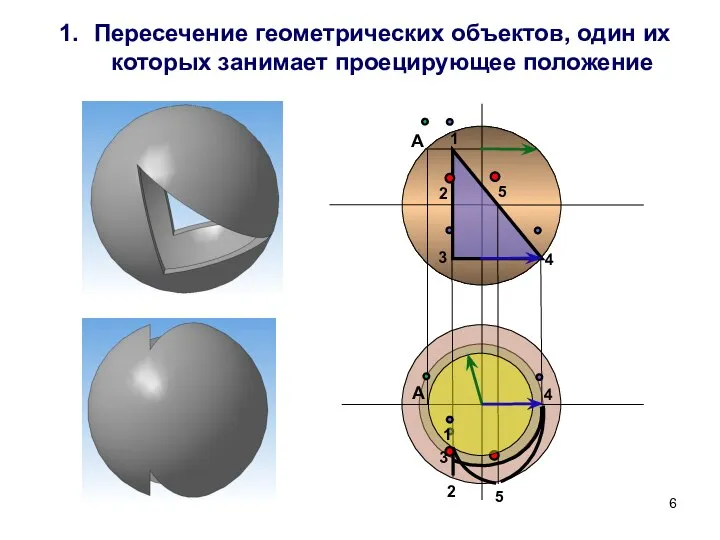
- 6. Пересечение геометрических объектов, один их которых занимает проецирующее положение 1 2 3 4 5 A A
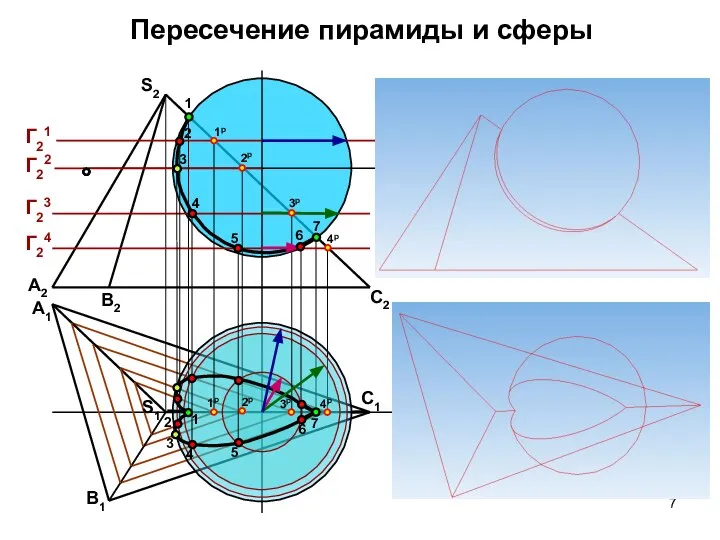
- 7. Пересечение пирамиды и сферы Г21 А2 В2 С2 S2 А1 В1 С1 S1 1 2 3
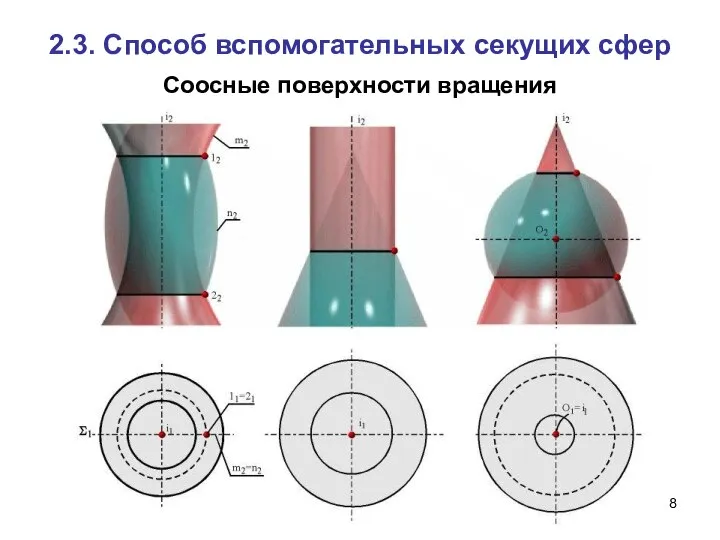
- 8. Соосные поверхности вращения 2.3. Способ вспомогательных секущих сфер
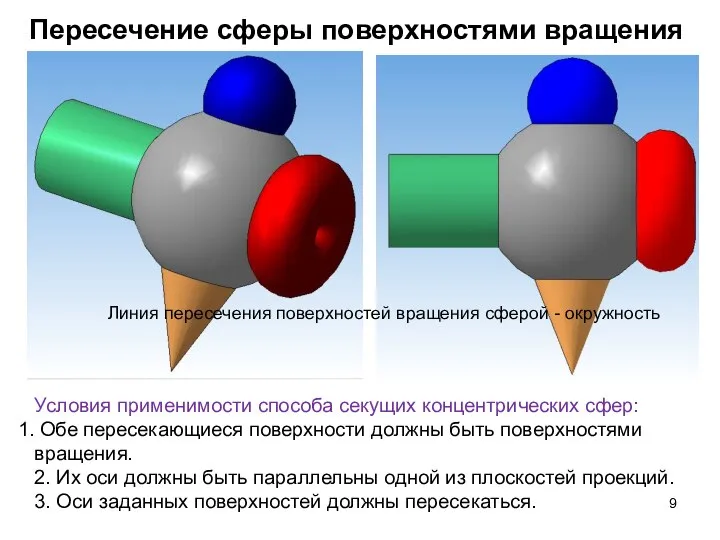
- 9. Пересечение сферы поверхностями вращения Линия пересечения поверхностей вращения сферой - окружность Условия применимости способа секущих концентрических
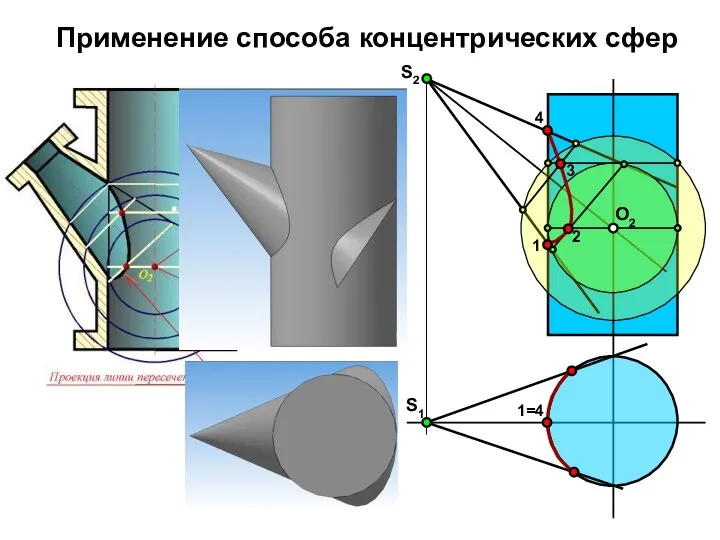
- 10. Применение способа концентрических сфер S2 S1 О2 1 2 3 4 1=4
- 11. 2.4. Теорема Монжа Если две поверхности второго порядка описаны около третьей поверхности (или вписаны в неё),
- 13. Скачать презентацию


 Знание - сила
Знание - сила Воздух - наш невидимый друг
Воздух - наш невидимый друг 200200.68.01 Прикладная оптика
200200.68.01 Прикладная оптика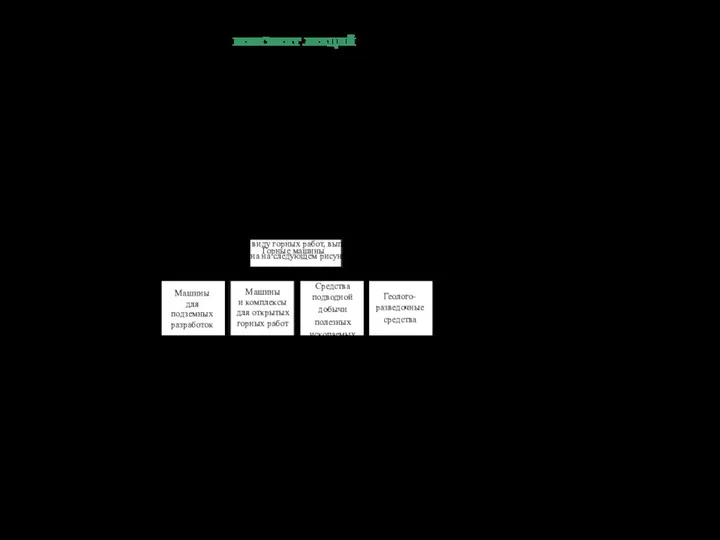 Горные машины и оборудование. Курс лекций
Горные машины и оборудование. Курс лекций Занятия Мои друзья. Мое увлечение
Занятия Мои друзья. Мое увлечение Характеристики проекта
Характеристики проекта Простые вещества-неметаллы
Простые вещества-неметаллы Кордицепс НСПCordyceps NSP
Кордицепс НСПCordyceps NSP ОЗ 7 Попередження ризиків від вибухонебезпечних предметів
ОЗ 7 Попередження ризиків від вибухонебезпечних предметів Реабилитация детей с девиантно-криминальным поведением
Реабилитация детей с девиантно-криминальным поведением Программирование на языке С
Программирование на языке С  Презентація
Презентація Актуальные проблемы формирования регионального свода книжных памятников Из опыта работы Архангельской областной научной биб
Актуальные проблемы формирования регионального свода книжных памятников Из опыта работы Архангельской областной научной биб Лекция 12. Особенная часть финансово-банковского права
Лекция 12. Особенная часть финансово-банковского права Нанесение тонких пленок из жидких растворов прекурсоров
Нанесение тонких пленок из жидких растворов прекурсоров Неделя
Неделя Управление качеством образования: компетенции 21 века. Эмоциональный интеллект
Управление качеством образования: компетенции 21 века. Эмоциональный интеллект РЕГИСТР РИСКОВ ПО КИРОВСКОЙ ОБЛАСТИ ПРИ ПОСТАВКАХ КОНТРОЛИРУЕМОЙ ДРЕВЕСИНЫ СОГЛАСНО ТРЕБОВАНИЯМ FSC Проект для обсуждения Пров
РЕГИСТР РИСКОВ ПО КИРОВСКОЙ ОБЛАСТИ ПРИ ПОСТАВКАХ КОНТРОЛИРУЕМОЙ ДРЕВЕСИНЫ СОГЛАСНО ТРЕБОВАНИЯМ FSC Проект для обсуждения Пров Шаблон проекта # бери своё
Шаблон проекта # бери своё МОУ «Афанасовская СОШ Корочанского района Белгородской области»
МОУ «Афанасовская СОШ Корочанского района Белгородской области»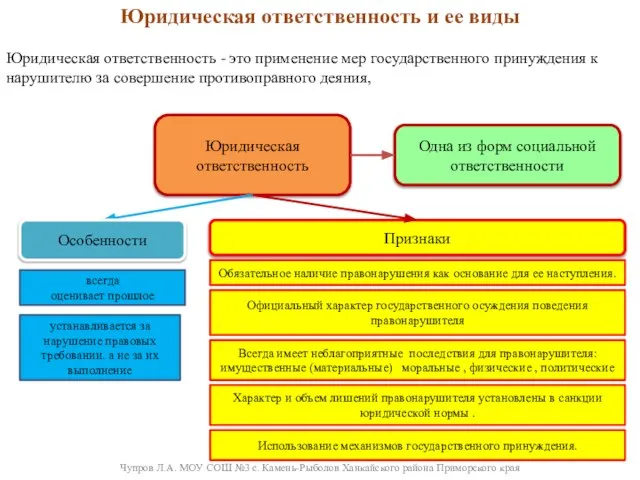 Юридическая ответственность и ее виды
Юридическая ответственность и ее виды Предупреждение Дженни Джозеф
Предупреждение Дженни Джозеф Аренда торгового помещения г. Астрахань
Аренда торгового помещения г. Астрахань В.Гюго
В.Гюго Тел. Офисный 8(3496)36-76-49 Галина.
Тел. Офисный 8(3496)36-76-49 Галина. Методическое письмо Об использовании результатов ЕГЭ 2009 года в преподавании математики в ОУ среднего (полного) общего образования
Методическое письмо Об использовании результатов ЕГЭ 2009 года в преподавании математики в ОУ среднего (полного) общего образования Презентация (1)
Презентация (1) Открытка ко дню пожилого человека
Открытка ко дню пожилого человека