Слайд 2
Наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод

последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности
Слайд 3
Система уравнений:
2x2+4x3 – x4=12
– x1+x2 – 2x3 – x 4=

– 15
4x1 – 8x3 – x4=12
2x1 – x2 – 4x3 – 2x4= – 3
Слайд 4Приведем данные уравнения к виду расширенной матрицы 5х4 этой системы

Слайд 5
Произведем следующие элементарные преобразования над ее строками:
а)перемножая все элементы первой строки

на 4 и 2
и прибавляя соответственно к 3 и 4 строкам, получаем требуемые нули в первом столбце матрицы
Слайд 6
б) в полученной матрице все элементы второй строки умножаем на (-2) и

прибавляем к третьей строке, затем делим все элементы второй строки на (-2) и прибавляем к четвертой, для получения необходимых нулей во втором столбце.
Слайд 7в) В полученной матрице все элементы четвертой строки делим на (-10)
и

перемножаем на 24
Слайд 8г) для получения необходимого нуля в третьем столбце в полученной матрице ко

всем элементам четвертой строки прибавляем соответствующие элементы третей строки
Слайд 9В полученной матрице для упрощения разделим третью строку на (-3),
а четвертую

умножим на 5
и разделим на (-27)
Слайд 10В результате всех этих преобразований данная матрица приводится к треугольному виду:

Слайд 11
Подставляя элементы преобразованной диагональной матрицы, получаем систему уравнений следующего вида:
-x1+x2–2x3–x4 = -15
2x2

+ 4x3 – x4 =12
8x3+x4=24
x4=4










 Пингвины (оригами)
Пингвины (оригами) Некоммерческое Партнерство Саморегулируемая организация «Межрегиональная гильдия управляющих компаний в жилищно-коммуна
Некоммерческое Партнерство Саморегулируемая организация «Межрегиональная гильдия управляющих компаний в жилищно-коммуна Межличностные отношения
Межличностные отношения Здравствуйте! Мы команда КУМ и C2O
Здравствуйте! Мы команда КУМ и C2O Стиль художественно литературы
Стиль художественно литературы Влияние сюжетно-ролевых игр на выстраивание диалога в семье и школе
Влияние сюжетно-ролевых игр на выстраивание диалога в семье и школе Основы переговорного процесса. Тема 5. Эффективные инструменты переговоров
Основы переговорного процесса. Тема 5. Эффективные инструменты переговоров Математическая игра Где чей домик
Математическая игра Где чей домик Юдакова Ирина Павловна
Юдакова Ирина Павловна Реки России
Реки России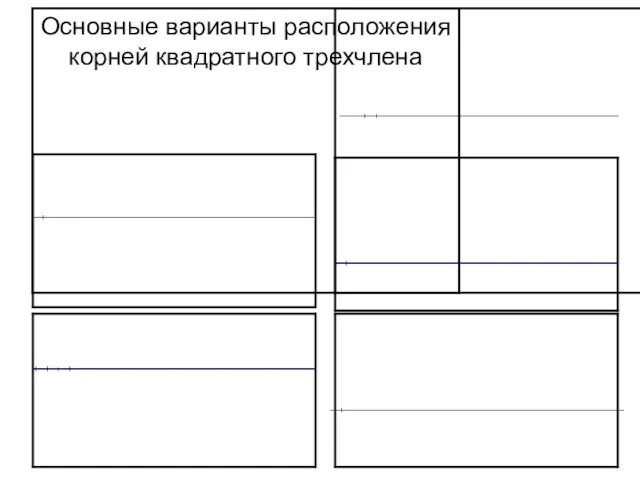 Основные варианты расположения корней квадратного трехчлена.
Основные варианты расположения корней квадратного трехчлена. Планирование и анализ требований
Планирование и анализ требований Okhta Sity PS 17062019
Okhta Sity PS 17062019 Проект Вот наша улица, дом наш родной
Проект Вот наша улица, дом наш родной Презентация на тему Московский Кремль
Презентация на тему Московский Кремль  Лошадка. Схема
Лошадка. Схема Породы деревьев, применяемые в деревянных конструкциях мебели, архитектуре, народных промыслах
Породы деревьев, применяемые в деревянных конструкциях мебели, архитектуре, народных промыслах Rich Fresh Affair
Rich Fresh Affair Мой прадед Марчук Федор Григорьевич- участник Великой Отечественной войны
Мой прадед Марчук Федор Григорьевич- участник Великой Отечественной войны Организация логопедической помощи детям в МДОУ Детский сад № 1 «Журавушка»
Организация логопедической помощи детям в МДОУ Детский сад № 1 «Журавушка» Японская и российская школы принятия управленческих решений
Японская и российская школы принятия управленческих решений последствия гидротехнических аварий или правила поведения во время и после гидротехнических аварий
последствия гидротехнических аварий или правила поведения во время и после гидротехнических аварий Великому человеку – великая память
Великому человеку – великая память Осторожно -ДЕТИ!
Осторожно -ДЕТИ! Стратегия. Коммуникационные цели
Стратегия. Коммуникационные цели Мои домашние питомцы
Мои домашние питомцы История развития гистологии, цитологии и эмбриологии. Развитие гистологии в Республике Казахстан
История развития гистологии, цитологии и эмбриологии. Развитие гистологии в Республике Казахстан Работы учащихся изостудии Зеркало г. Златоуст
Работы учащихся изостудии Зеркало г. Златоуст