Решение систем уравнений

Цель работы: .
По страницам учебников А.Г. Мордковича «Алгебра 7 и 9 классов» проанализировать рассмотренные в них методы решения систем уравнений.
Исследовать некоторые способы решений систем уравнений за страницами учебника.
Показать своей работой, что решать системы уравнений очень просто.

выявить основные способы решения систем линейных уравнений, рассматриваемых в учебнике А.Г. Мордковича «Алгебра -7»
проиллюстрировать примерами каждый способ.
расширить свои познания о других способах решения систем линейных уравнений.
ввести понятие систем рациональных уравнений.
рассмотреть основные методы решения систем рациональных уравнений по учебнику А.Г. Мордковича «Алгебра- 9».
проиллюстрировать теоретический материал удачными примерами.
рассмотреть новый вид – симметрические системы.
разобраться в методах решения этого вида.
Задачи работы:.

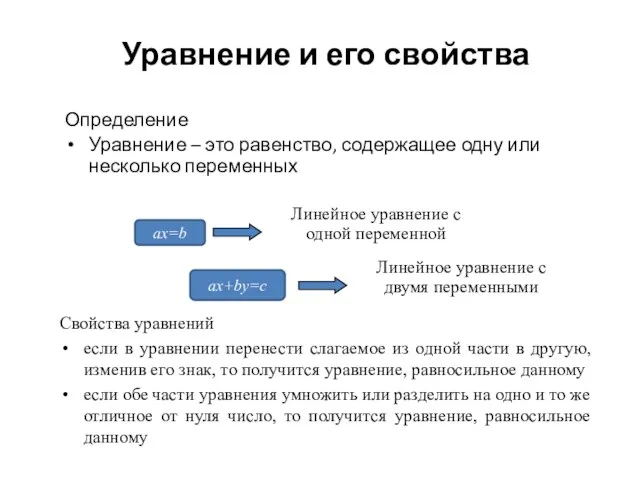
Определение
Уравнение – это равенство, содержащее одну или несколько переменных
Линейное уравнение с
одной переменной
Линейное уравнение с
двумя переменными
Свойства уравнений
если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному
если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному
Уравнение и его свойства
ax=b
ax+by=c

Определения
Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно
Каждая пара значений переменных, которая одновременно является решением всех уравнений системы, называется решением системы
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство
Решить систему уравнений - это значит найти все её решения или установить, что их нет
Система уравнений и её решение

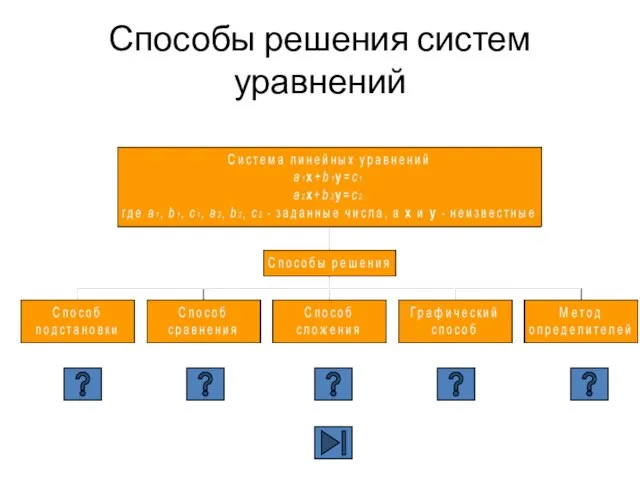
Способы решения систем уравнений

Способ подстановки (алгоритм)
Из какого-либо уравнения выразить одну переменную через другую
Подставить полученное выражение для переменной в другое уравнение и решить его
Сделать подстановку найденного значения переменной и вычислить значение второй переменной
Записать ответ: х=…; у=… .

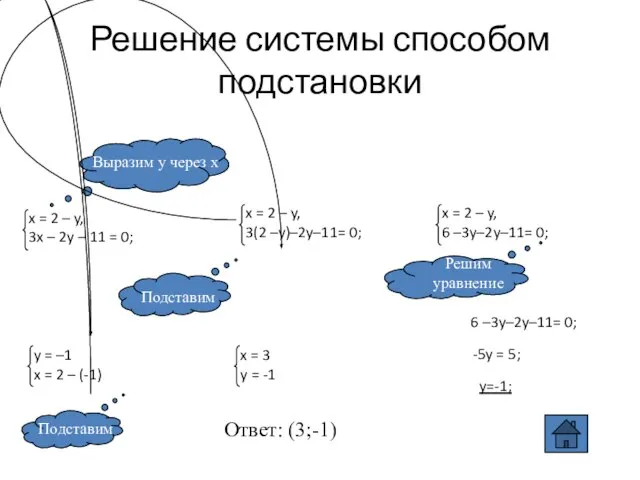
Решение системы способом подстановки
6 –3y–2y–11= 0;
-5y = 5;
y=-1;
Ответ: (3;-1)
x = 2 – y,
3(2 –y)–2y–11= 0;
x = 2 – y,
3x – 2y – 11 = 0;
x = 2 – y,
6 –3y–2y–11= 0;
y = –1
x = 2 – (-1)
x = 3
y = -1

Способ сравнения (алгоритм)
Выразить у через х (или х через у) в каждом уравнении
Приравнять выражения, полученные для одноимённых переменных
Решить полученное уравнение и найти значение одной переменной
Подставить значение найденной переменной в одно из выражений для другой переменной и найти её значение
Записать ответ: х=…; у=… .

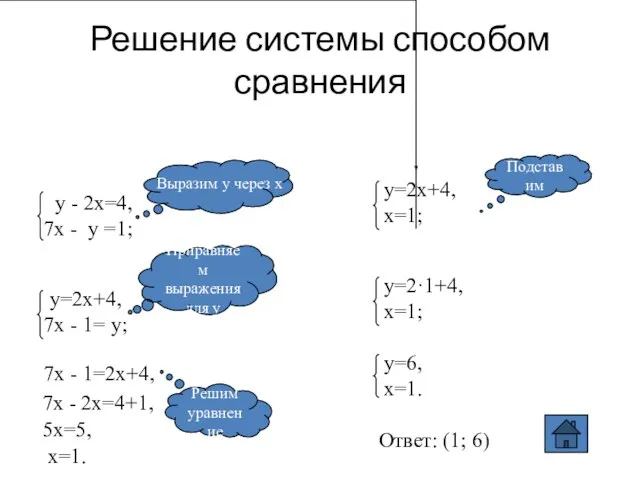
Решение системы способом сравнения
Приравняем
выражения
для у
7х - 1=2х+4,
7х - 2х=4+1,
5х=5,
х=1.
Решим
уравнение
Ответ: (1; 6)

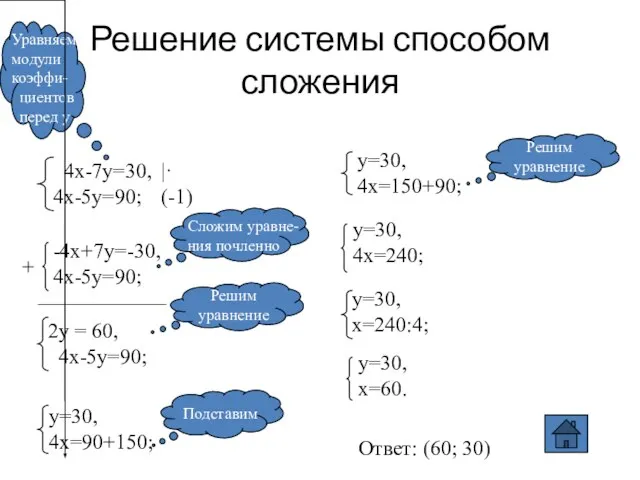
Способ сложения (алгоритм)
Уравнять модули коэффициентов при какой-нибудь переменной
Сложить почленно уравнения системы
Составить новую систему: одно уравнение новое, другое - одно из старых
Решить новое уравнение и найти значение одной переменной
Подставить значение найденной переменной в старое уравнение и найти значение другой переменной
Записать ответ: х=…; у=… .

Решение системы способом сложения
|·(-1)
+
____________
Ответ: (60; 30)

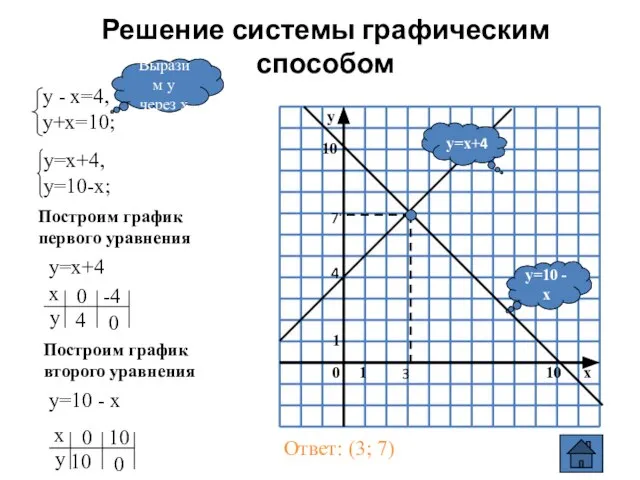
Графический способ (алгоритм)
Выразить у через х в каждом уравнении
Построить в одной системе координат график каждого уравнения
Определить координаты точки пересечения
Записать ответ: х=…; у=… , или (х; у)

Решение системы графическим способом
y=10 - x
y=x+4
Выразим у
через х
Построим график
первого уравнения
у=х+4
Построим график
второго уравнения
у=10 - х
Ответ: (3; 7)
4
3
7
4

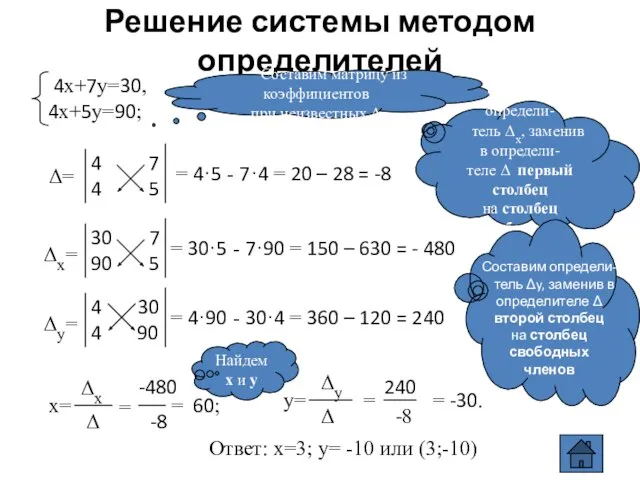
Метод определителей (алгоритм)
Составить табличку (матрицу) коэффициентов при неизвестных и вычислить определитель .
Найти - определитель x, получаемый из  заменой первого столбца на столбец свободных членов.
Найти - определитель y, получаемый из  заменой второго столбца на столбец свободных членов.
Найти значение переменной х по формуле x / .
Найти значение переменной у по формуле y / .
Записать ответ: х=…; у=… .

240
Решение системы методом определителей
Составим матрицу из коэффициентов
при неизвестных 
= 4·5 - 7·4 = 20 – 28 = -8
= 30·5 - 7·90 = 150 – 630 = - 480
= 4·90 - 30·4 = 360 – 120 = 240
Составим определи-
тель x, заменив в определи-
теле  первый столбец
на столбец свободных
членов
x
х=

=
-480
-8
=
60;
у=
y

=
-8
= -30.
Найдем
х и у
Ответ: х=3; у= -10 или (3;-10)
Составим определи-
тель y, заменив в определителе  второй столбец
на столбец свободных
членов

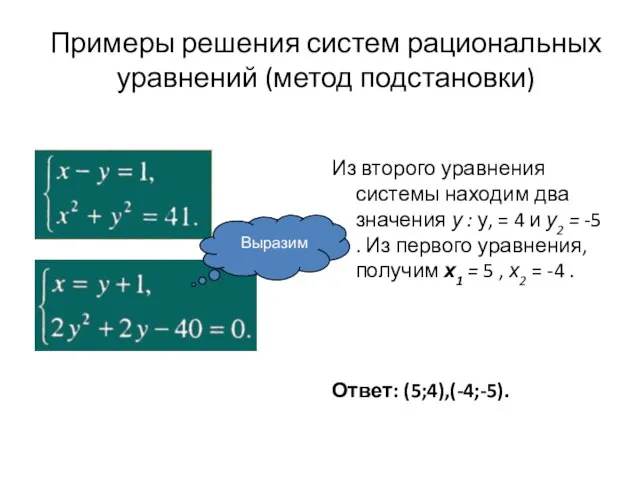
Системы рациональных уравнений
Рациональным уравнением с двумя переменными х и у называют уравнения вида р(х, у) = 0, где р(х, у) – рациональное выражение.
Системы рациональных уравнений, изучаемые в 9-ом классе, так же можно решать выше предложенными способами.

Примеры решения систем рациональных уравнений (метод подстановки)
Из второго уравнения системы находим два значения у : у, = 4 и у2 = -5 . Из первого уравнения, получим х1 = 5 , х2 = -4 .
Ответ: (5;4),(-4;-5).
Выразим

Алгоритм метода введения новой переменной
Замени одно или два выражения в уравнениях системы новыми переменными так, чтобы вновь полученные уравнения стали более простыми.
Реши полученную систему уравнений методом, наиболее подходящим для этой системы уравнений.
Сделай обратную замену, для того, чтобы найти значения первоначальных переменных.
Запиши ответ в виде пар значений (x,y), которые были найдены на третьем шаге.

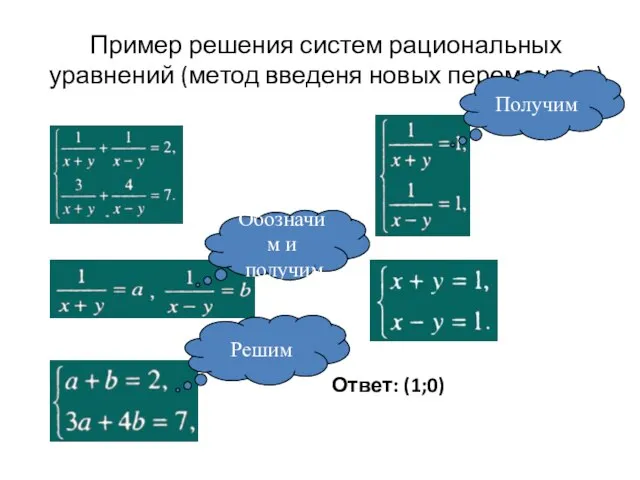
Пример решения систем рациональных уравнений (метод введеня новых переменных)
Ответ: (1;0)
Обозначим и
получим
Решим
Получим

Возвратные уравнения
Уравнение вида anxn+an–1xn–1 +…+a1x+a0=0
называется возвратным,
если его коэффициенты, стоящие на симметричных позициях, равны, то есть если an – 1 = ak, при k = 0, 1, …, n.

Симметрические системы уравнений
Система с n неизвестными называется симметрической, если она не меняется при перестановки неизвестных.
Симметрическая система двух уравнений с двумя неизвестными х и у решается подстановкой
u = х + у , v = ху (Заметим, что встречающиеся выражения в симметрических системах выражаются через u и v).

Примеры решения симметрических систем уравнений
х2 + ху + у2 =13,
х + у = 4
Пусть х + у = u, ху = v.
u2 – v = 13,
u = 4
16 – v = 13,
u = 4
v = 3,
u = 4
х + у = 4,
ху = 3
х = 4 – у
ху = 3
х = 4 – у,
(4 – у) у = 3
х = 4 – у, x=4-y,
у1 = 3; у2 = 1
х1 = 1, х2 = 3,
у1 = 3, у2 = 1
Ответ: (1; 3); (3; 1).

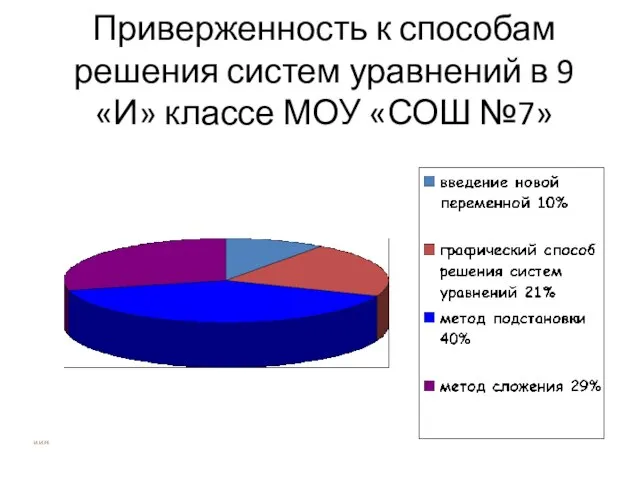
Приверженность к способам решения систем уравнений в 9 «И» классе МОУ «СОШ №7»
И.И.Н.