Содержание
- 2. Признаки равенства треугольников Треугольник на евклидовой плоскости однозначно можно определить по следующим тройкам основных элементов: Равенство
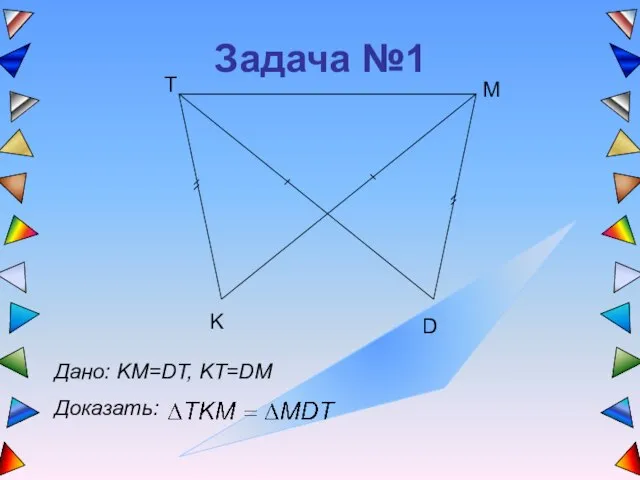
- 3. Задача №1 T K D M Дано: KM=DT, KT=DM Доказать:
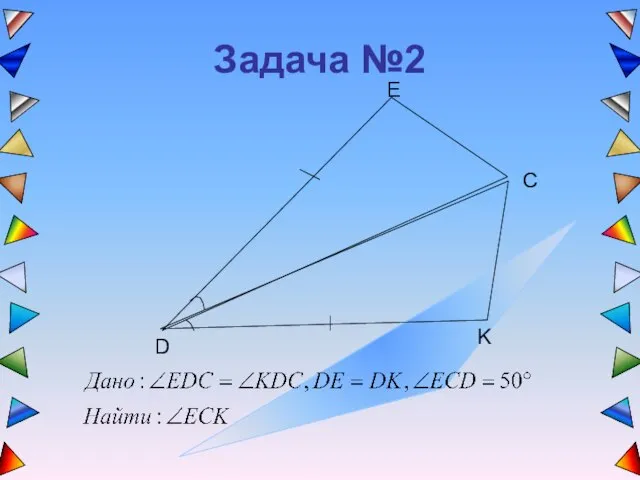
- 4. Задача №2 E D K C
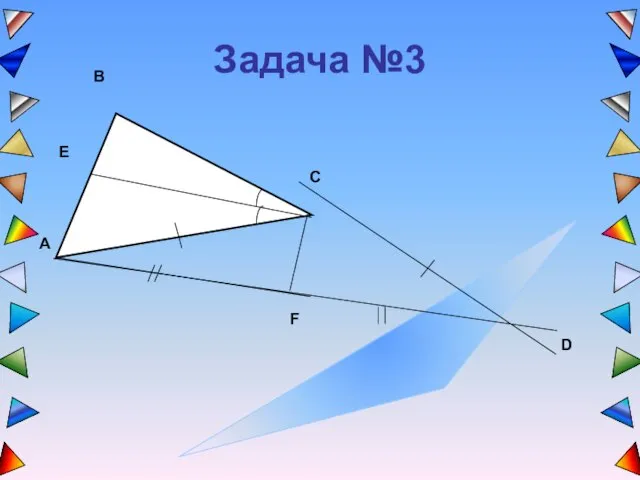
- 5. Задача №3
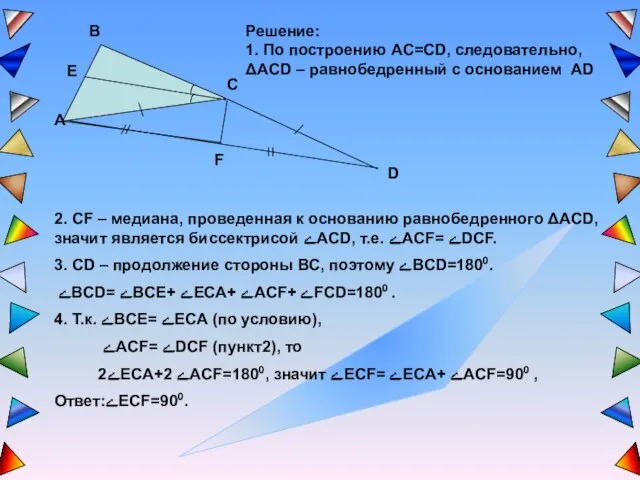
- 6. Решение: 1. По построению AC=CD, следовательно, ΔACD – равнобедренный с основанием AD 2. CF – медиана,
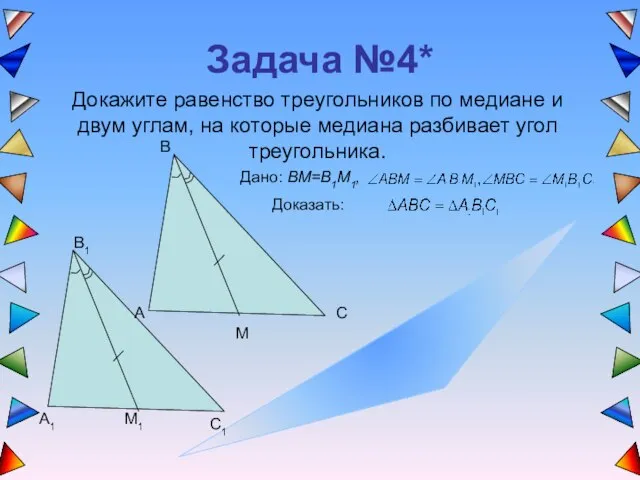
- 7. Задача №4* Докажите равенство треугольников по медиане и двум углам, на которые медиана разбивает угол треугольника.
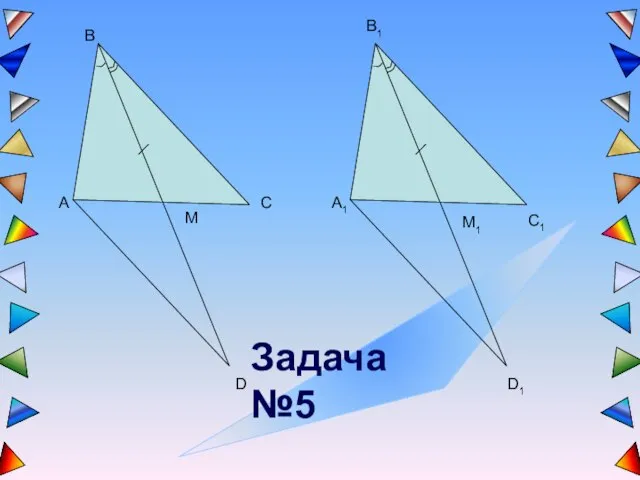
- 8. A B C M B1 A1 M1 C1 D D1 Задача №5
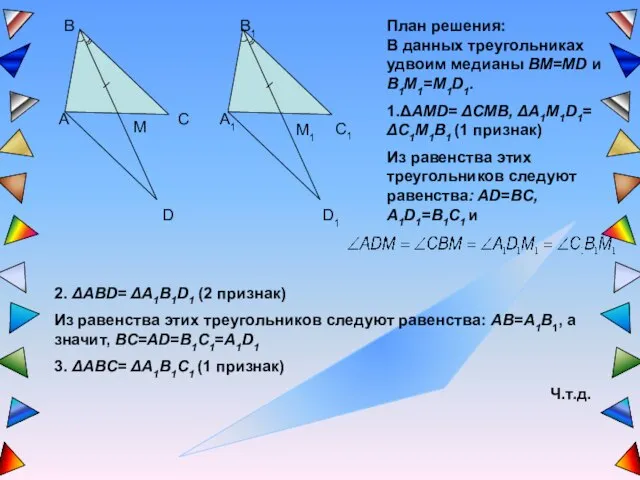
- 9. План решения: В данных треугольниках удвоим медианы BM=MD и B1M1=M1D1. 1.ΔAMD= ΔCMB, ΔA1M1D1= ΔC1M1B1 (1 признак)
- 11. Скачать презентацию

 Дегустация шоколада и шоколадно-ореховой пасты СТМ О’КЕЙ
Дегустация шоколада и шоколадно-ореховой пасты СТМ О’КЕЙ РЫНОК НЕДВИЖИМОСТИ ГЛАЗАМИ ПОКУПАТЕЛЕЙ(краткие результаты исследования)
РЫНОК НЕДВИЖИМОСТИ ГЛАЗАМИ ПОКУПАТЕЛЕЙ(краткие результаты исследования) Возможности для профессионального развития
Возможности для профессионального развития Реабилитационный центр для наркозависимых людей Возрождение
Реабилитационный центр для наркозависимых людей Возрождение ПО для создания и редактирования мультимедийных презентаций (OpenOffice.org Impress)
ПО для создания и редактирования мультимедийных презентаций (OpenOffice.org Impress) Mothers' Day
Mothers' Day БОЛЬШИЕ ДЕНЬГИ В ВАШЕЙ ЖИЗНИ, СЕТЕВОЙ МАРКЕТИНГ
БОЛЬШИЕ ДЕНЬГИ В ВАШЕЙ ЖИЗНИ, СЕТЕВОЙ МАРКЕТИНГ Творчество В. М. Васнецова, М. А. Врубеля, М.В. Нестерова. История искусства. Часть 17
Творчество В. М. Васнецова, М. А. Врубеля, М.В. Нестерова. История искусства. Часть 17 Шахматная викторина
Шахматная викторина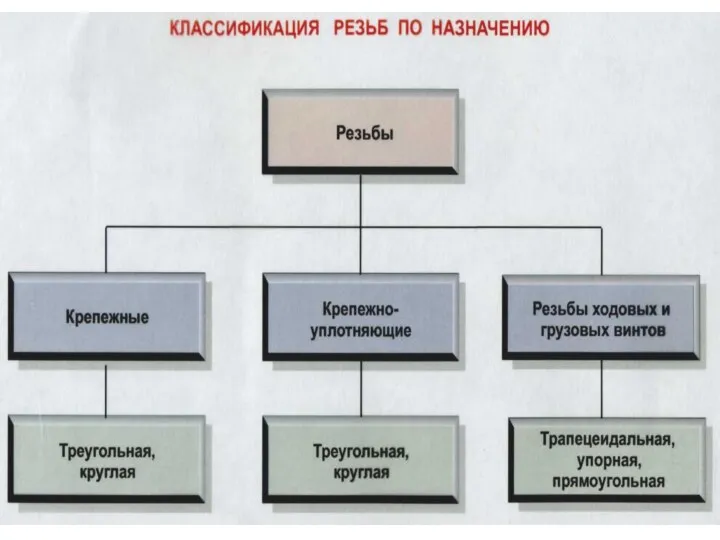 Классификация резьб по назначению
Классификация резьб по назначению Наименование организации
Наименование организации Дистанционное обучение лиц с ОВЗ (периферические устройства, адаптированные к различным диагнозам)
Дистанционное обучение лиц с ОВЗ (периферические устройства, адаптированные к различным диагнозам) Вкус жизни…
Вкус жизни… АП_СТИЛЬ
АП_СТИЛЬ Центр сопровождения проектов "Открытие"
Центр сопровождения проектов "Открытие" Кружок по математике 5 «а» класс
Кружок по математике 5 «а» класс Стратегический план Агентства Республики Казахстанпо информатизации и связи на 2009-2011 годы
Стратегический план Агентства Республики Казахстанпо информатизации и связи на 2009-2011 годы Remade iPhone в Цитрусе
Remade iPhone в Цитрусе ПРИЧИНЫ ВОЗНИКНОВЕНИЯ ПОЖАРОВ В ЖИЛЫХ И ОБЩЕСТВЕННЫХ ЗДАНИЯХ.
ПРИЧИНЫ ВОЗНИКНОВЕНИЯ ПОЖАРОВ В ЖИЛЫХ И ОБЩЕСТВЕННЫХ ЗДАНИЯХ. Одобрение Онлайн по объектам на Витрине ДомКлик. Сбербанк
Одобрение Онлайн по объектам на Витрине ДомКлик. Сбербанк 4
4 13-ое Российское совещание «Безопасность исследовательских ядерных установок»
13-ое Российское совещание «Безопасность исследовательских ядерных установок» Возвращение из вавилонского плена
Возвращение из вавилонского плена Natural Disasters
Natural Disasters КАТАЛОГ РОССИЙСКИХ ЭЛЕКТРОННЫХ ПЕРИОДИЧЕСКИХ ИЗДАНИЙ
КАТАЛОГ РОССИЙСКИХ ЭЛЕКТРОННЫХ ПЕРИОДИЧЕСКИХ ИЗДАНИЙ Изготовление прихватки. Лоскутное шитье
Изготовление прихватки. Лоскутное шитье Информационные технологии
Информационные технологии Презентация на тему Теория относительности
Презентация на тему Теория относительности