Сфера, вписанная в многогранник

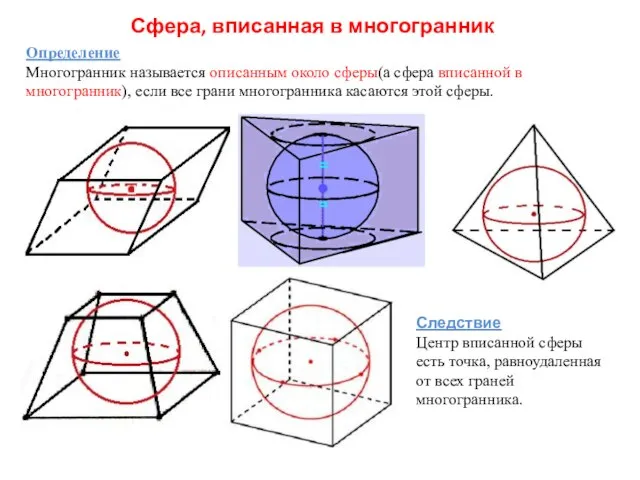
Сфера, вписанная в многогранник
Определение
Многогранник называется описанным около сферы(а сфера вписанной в многогранник), если все грани многогранника касаются этой сферы.
Следствие
Центр вписанной сферы есть точка, равноудаленная от всех граней многогранника.

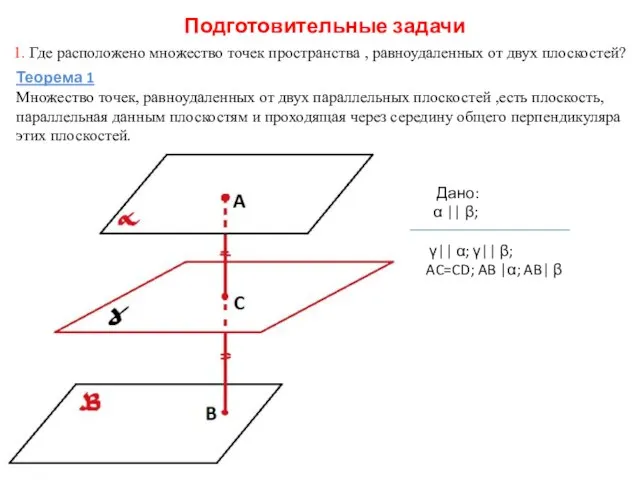
Подготовительные задачи
1. Где расположено множество точек пространства , равноудаленных от двух плоскостей?
Теорема 1
Множество точек, равноудаленных от двух параллельных плоскостей ,есть плоскость, параллельная данным плоскостям и проходящая через середину общего перпендикуляра этих плоскостей.
Дано:
α || β;
γ|| α; γ|| β;
AC=CD; AB |α; AB| β

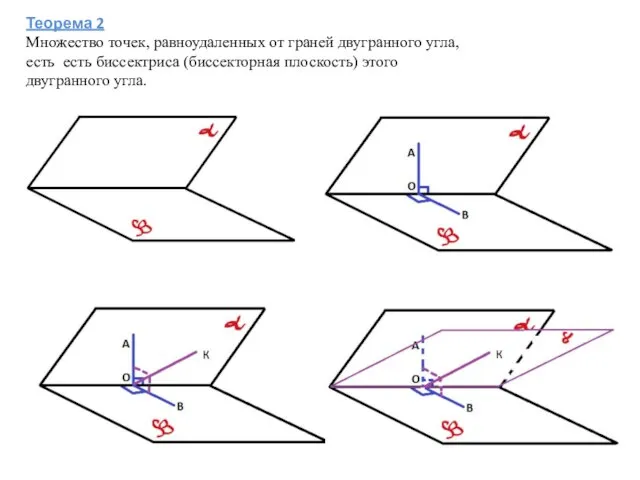
Теорема 2
Множество точек, равноудаленных от граней двугранного угла, есть есть биссектриса (биссекторная плоскость) этого двугранного угла.

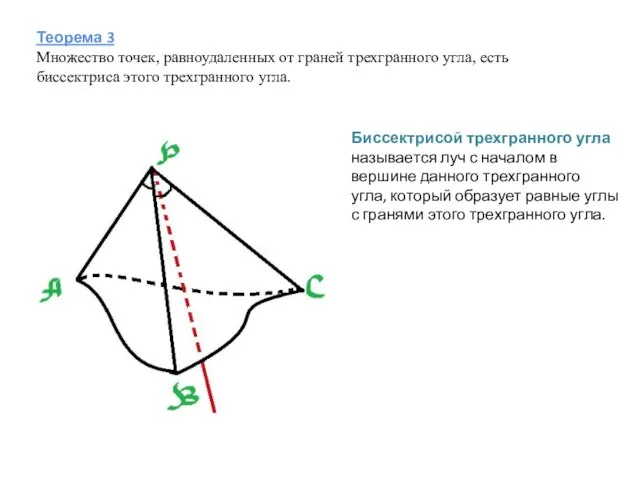
Теорема 3
Множество точек, равноудаленных от граней трехгранного угла, есть биссектриса этого трехгранного угла.
Биссектрисой трехгранного угла называется луч с началом в вершине данного трехгранного угла, который образует равные углы с гранями этого трехгранного угла.

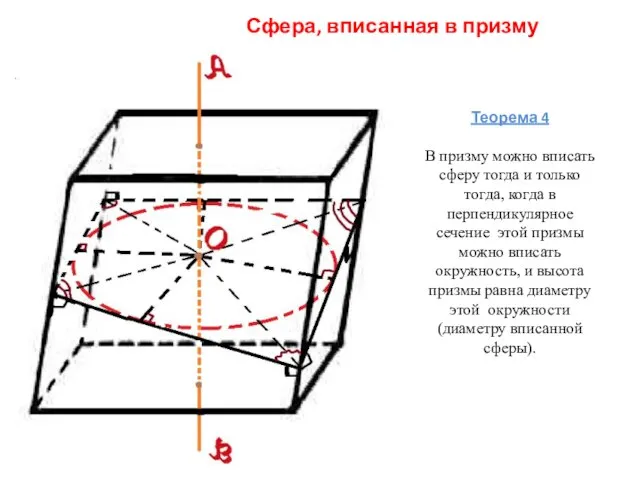
Сфера, вписанная в призму
Теорема 4
В призму можно вписать сферу тогда и только тогда, когда в перпендикулярное сечение этой призмы можно вписать окружность, и высота призмы равна диаметру этой окружности (диаметру вписанной сферы).

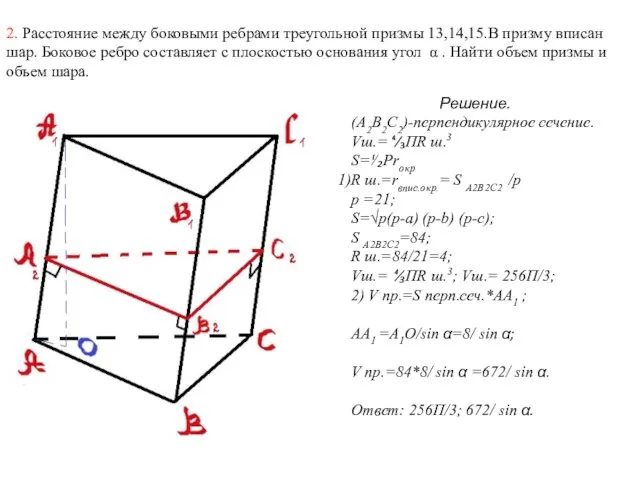
2. Расстояние между боковыми ребрами треугольной призмы 13,14,15.В призму вписан шар. Боковое ребро составляет с плоскостью основания угол α . Найти объем призмы и объем шара.
Решение.
(А2В2С2)-перпендикулярное сечение.
Vш.= ⁴⁄₃ПR ш.3
S=⅟₂Prокр
R ш.=rвпис.окр.= S А2В2С2 /p
p =21;
S=√p(p-a) (p-b) (p-c);
S А2В2С2=84;
R ш.=84/21=4;
Vш.= ⁴⁄₃ПR ш.3; Vш.= 256П/3;
2) V пр.=S перп.сеч.*АА1 ;
АА1 =А1О/sin α=8/ sin α;
V пр.=84*8/ sin α =672/ sin α.
Ответ: 256П/3; 672/ sin α.

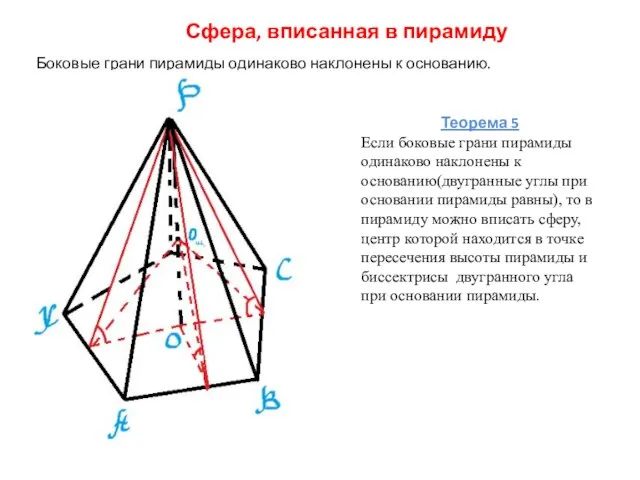
Сфера, вписанная в пирамиду
Боковые грани пирамиды одинаково наклонены к основанию.
Теорема 5
Если боковые грани пирамиды одинаково наклонены к основанию(двугранные углы при основании пирамиды равны), то в пирамиду можно вписать сферу, центр которой находится в точке пересечения высоты пирамиды и биссектрисы двугранного угла при основании пирамиды.

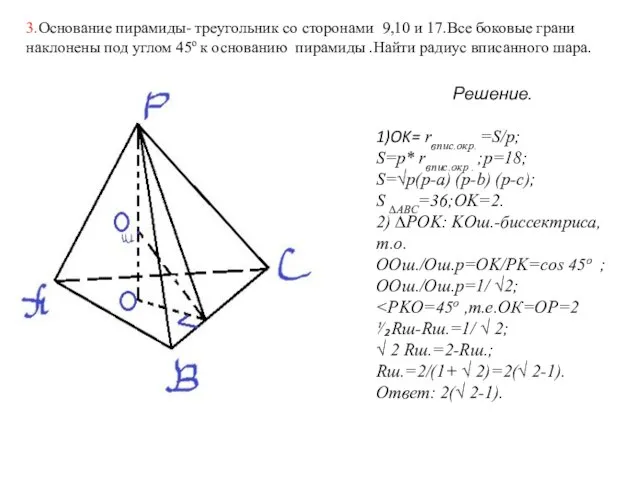
3.Основание пирамиды- треугольник со сторонами 9,10 и 17.Все боковые грани наклонены под углом 45о к основанию пирамиды .Найти радиус вписанного шара.
Решение.
1)OK= rвпис.окр. =S/p;
S=p* rвпис.окр . ;p=18;
S=√p(p-a) (p-b) (p-c);
S ∆АВС=36;OK=2.
2) ∆POK: KOш.-биссектриса, т.о.
ООш./Ош.p=OK/PK=cos 45о ;
ООш./Ош.p=1/ √2;
⅟₂Rш-Rш.=1/ √ 2;
√ 2 Rш.=2-Rш.;
Rш.=2/(1+ √ 2)=2(√ 2-1).
Ответ: 2(√ 2-1).

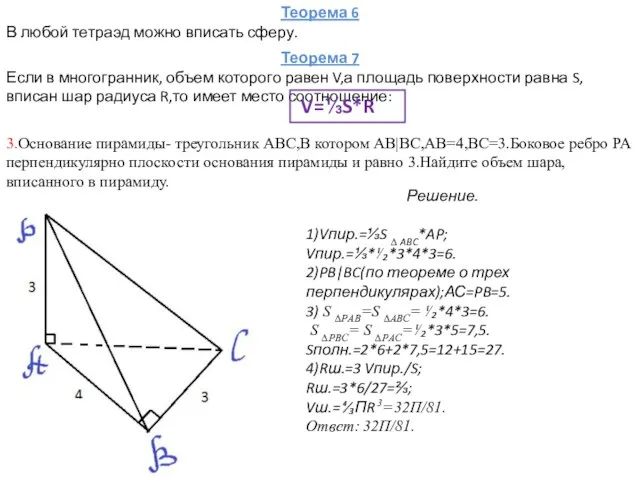
Теорема 6
В любой тетраэд можно вписать сферу.
Теорема 7
Если в многогранник, объем которого равен V,а площадь поверхности равна S,вписан шар радиуса R,то имеет место соотношение:
V=⅓S*R
3.Основание пирамиды- треугольник АВС,В котором АВ|ВС,АВ=4,ВС=3.Боковое ребро РА перпендикулярно плоскости основания пирамиды и равно 3.Найдите объем шара, вписанного в пирамиду.
Решение.
1)Vпир.=⅓S ∆ ABC*AP;
Vпир.=⅓*⅟₂*3*4*3=6.
2)PB|BC(по теореме о трех перпендикулярах);АС=PB=5.
3) S ∆PАВ=S ∆АВС= ⅟₂*4*3=6.
S ∆PВC= S ∆PАC=⅟₂*3*5=7,5.
Sполн.=2*6+2*7,5=12+15=27.
4)Rш.=3 Vпир./S;
Rш.=3*6/27=⅔;
Vш.=⁴⁄₃ПR 3=32П/81.
Ответ: 32П/81.

4. Шар вписан в прямую призму, основание которой- равнобедренная трапеция с основаниями 2 и 8.Найдите объем шара и объем призмы.
Решение.
1)Rш.= rвпис.окр . ;Hпр.=D впис.окр.=CK.
2)DC+AB=AD+CB;
2BC=2+8; BC=5.
3)BC=⅟₂(AB-DC); BK= ⅟₂(8-2)=3;
4) ∆BCK:CK=4; Rш.=2.
5)Vпр.=Sосн.*Нпр.;
Vпр.=80;
Vш.= ⁴⁄₃ПR 3 ;
Vш.= ⁴⁄₃П2 3 =32П/3.
Ответ: 32П/3.