Решение задач на законы сохранения импульса и энергии

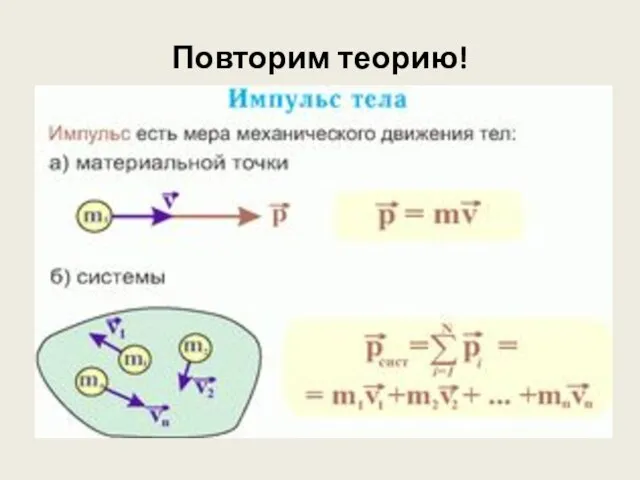
Повторим теорию!

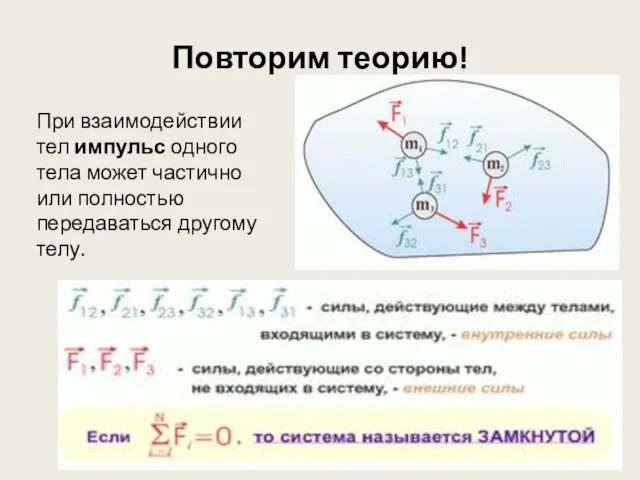
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу.
Повторим теорию!

Повторим теорию!
для неупругого взаимодействия
для упругого взаимодействия

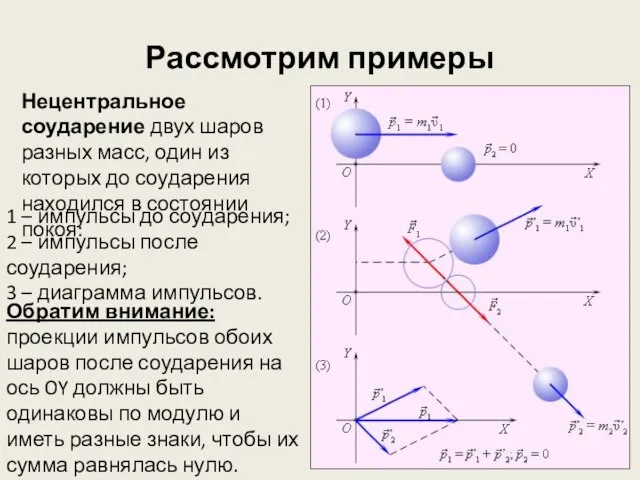
Нецентральное соударение двух шаров разных масс, один из которых до соударения находился в состоянии покоя:
Рассмотрим примеры
1 – импульсы до соударения;
2 – импульсы после соударения;
3 – диаграмма импульсов.
Обратим внимание: проекции импульсов обоих шаров после соударения на ось OY должны быть одинаковы по модулю и иметь разные знаки, чтобы их сумма равнялась нулю.

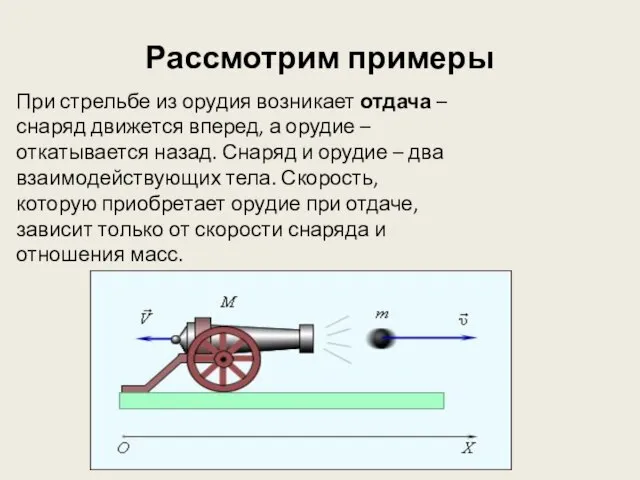
Рассмотрим примеры
При стрельбе из орудия возникает отдача – снаряд движется вперед, а орудие – откатывается назад. Снаряд и орудие – два взаимодействующих тела. Скорость, которую приобретает орудие при отдаче, зависит только от скорости снаряда и отношения масс.

Рассмотрим примеры
На принципе отдачи основано реактивное движение. В ракете при сгорании топлива газы, нагретые до высокой температуры, выбрасываются из сопла с большой скоростью относительно ракеты.

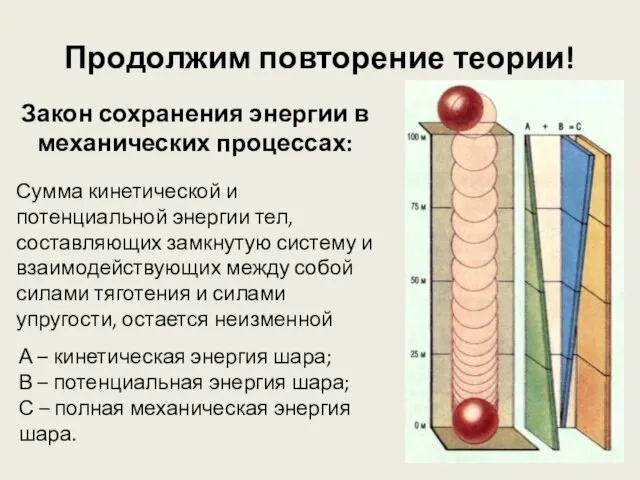
Продолжим повторение теории!
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела
Теорема о кинетической энергии тела: работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии
A = Ek2 – Еk1
Потенциальная энергия тела в поле силы тяжести равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень
Ep = mgh
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией

Продолжим повторение теории!
Закон сохранения энергии в механических процессах:
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной
А – кинетическая энергия шара;
В – потенциальная энергия шара;
С – полная механическая энергия шара.

Образовательный портал «Мой университет» - www.moi-universitet.ru
Факультет «Реформа образования» - wwwwww.www.eduwww.edu-www.edu-reformawww.edu-reforma.www.edu-reforma.ru
Неупругие и упругие соударения
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.

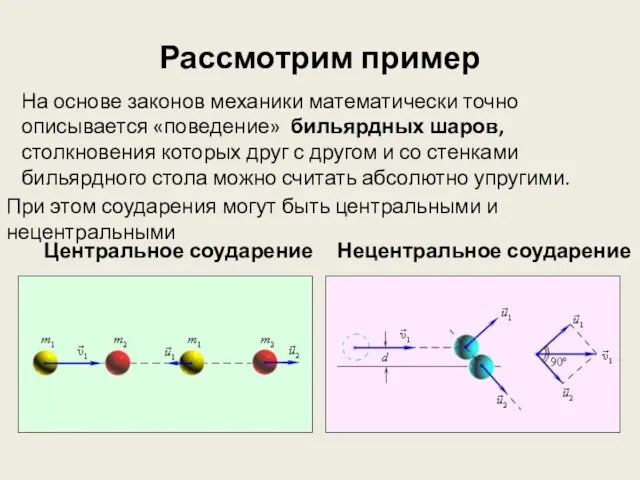
Рассмотрим пример
На основе законов механики математически точно описывается «поведение» бильярдных шаров, столкновения которых друг с другом и со стенками бильярдного стола можно считать абсолютно упругими.
При этом соударения могут быть центральными и нецентральными
Центральное соударение
Нецентральное соударение

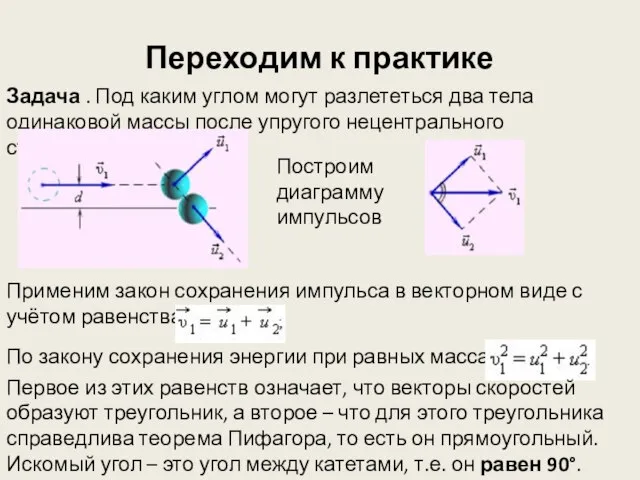
Переходим к практике
Задача . Под каким углом могут разлететься два тела одинаковой массы после упругого нецентрального столкновения?
Построим диаграмму импульсов
Применим закон сохранения импульса в векторном виде с учётом равенства масс:
По закону сохранения энергии при равных массах:
Первое из этих равенств означает, что векторы скоростей образуют треугольник, а второе – что для этого треугольника справедлива теорема Пифагора, то есть он прямоугольный. Искомый угол – это угол между катетами, т.е. он равен 90°.