РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ

Задача о планированиии производства
Фабрика выпускает 3 вида изделий:
изделие А, изделие В, изделие С.
Прибыль от продажи 1 шт. изделия А составляет 13 у.е., изделия В – 18 у.е. и изделия С – 22 у.е.
Найти оптимальные объемы выпуска трех видов продукции для получения максимальной прибыли от их продажи.
При решении данной задачи должны быть учтены следующие ограничения:
общий объем производства – всего 300 изделий;
должно быть произведено не менее 50 изделий А;
должно быть произведено не менее 40 изделий В;
должно быть произведено не более 40 изделий С.

ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Переменные модели
ХА, ХВ , ХС– объемы производства изделий А, В и С соответсвенно
Целевая функнция:
13* ХА +18* ХВ +22 * ХС
Ограничения:
ХА ≥ 50, ХВ ≥ 40, 0 ≤ ХС≤ 40,
ХА + ХВ +ХС = 300

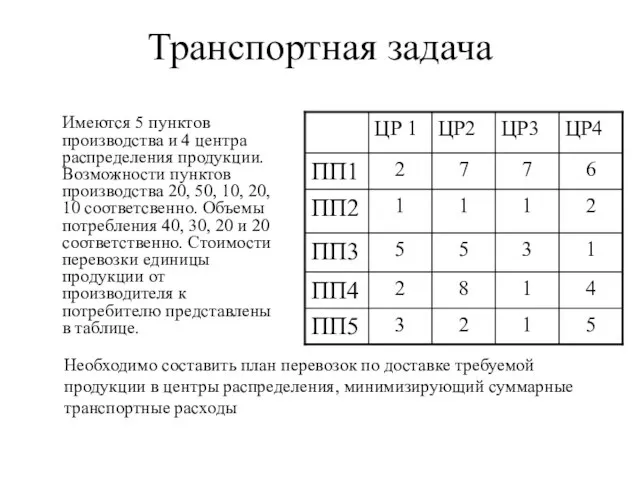
Транспортная задача
Имеются 5 пунктов производства и 4 центра распределения продукции. Возможности пунктов производства 20, 50, 10, 20, 10 соответсвенно. Объемы потребления 40, 30, 20 и 20 соответственно. Стоимости перевозки единицы продукции от производителя к потребителю представлены в таблице.
Необходимо составить план перевозок по доставке требуемой продукции в центры распределения, минимизирующий суммарные транспортные расходы

Построение математической модели
Переменные модели
Хij – объем перевозок с пункта производства в центр распределения
Целевая функция
Ограничения
Хij≥0
Вся продукция должна быть вывезена и все потребности центров распределения должны быть удовлетворены

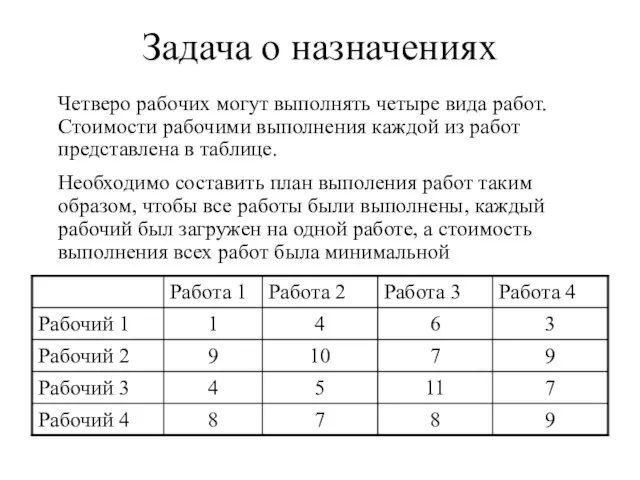
Задача о назначениях
Четверо рабочих могут выполнять четыре вида работ. Стоимости рабочими выполнения каждой из работ представлена в таблице.
Необходимо составить план выполения работ таким образом, чтобы все работы были выполнены, каждый рабочий был загружен на одной работе, а стоимость выполнения всех работ была минимальной

Математическая модель
Переменные модели :
Xij = 0, если i-м рабочим не выполняется j-я работа
Xij = 1, если i-м рабочим выполняется j-я работа
Целевая функция :
Ограничения:
Xij – могут принимать значения 0 или 1

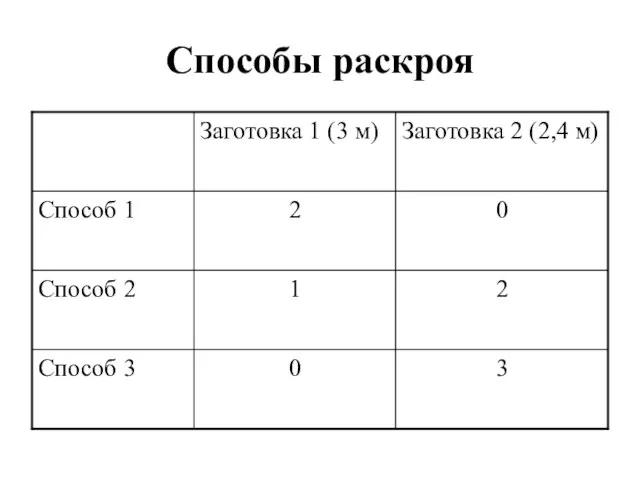
Задача о раскрое
Прутки длиной 8 метров разрезаются на заготовки длиной 3 и 2.4 м, Заготовок первого типа нужно получить не менее 25 штук, а второго - не менее 36 штук.
Определить минимальное число разрезаемых прутков. Допускаются лишь способы разрезки, при которых длина остатка меньше любой заготовки.

Способы раскроя

Математическая модель
Переменные модели:
X1, X2, X3 - количество прутков, разрезаных способами 1, 2 и 3 соответсвенно
Целевая функция: X1+ X2+ X3
Ограничения:
X1, X2, X3 –целочисленные
X1 ≥ 0, X2 ≥ 0, X3 ≥ 0
Количество заготовок 1 ≥ 25
Количество заготовок 1 ≥ 25

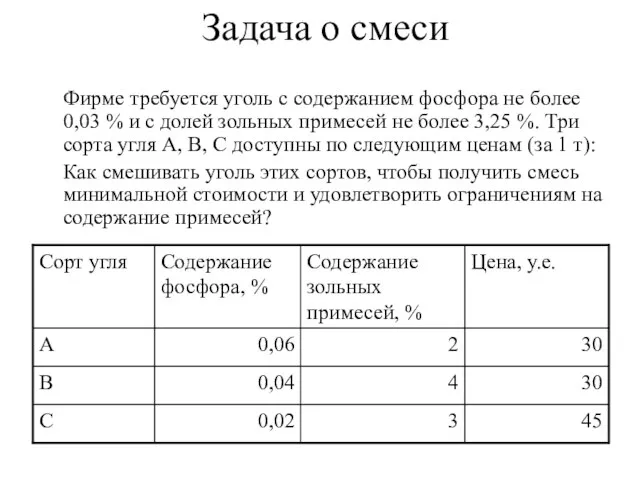
Задача о смеси
Фирме требуется уголь с содержанием фосфора не более 0,03 % и с долей зольных примесей не более 3,25 %. Три сорта угля A, B, C доступны по следующим ценам (за 1 т):
Как смешивать уголь этих сортов, чтобы получить смесь минимальной стоимости и удовлетворить ограничениям на содержание примесей?