Решение задач по теме «Теорема Пифагора»

ЦЕЛИ УРОКА:
Научиться применять теорему Пифагора, теорему, обратную теореме Пифагора, опорные формулы к решению различных задач.

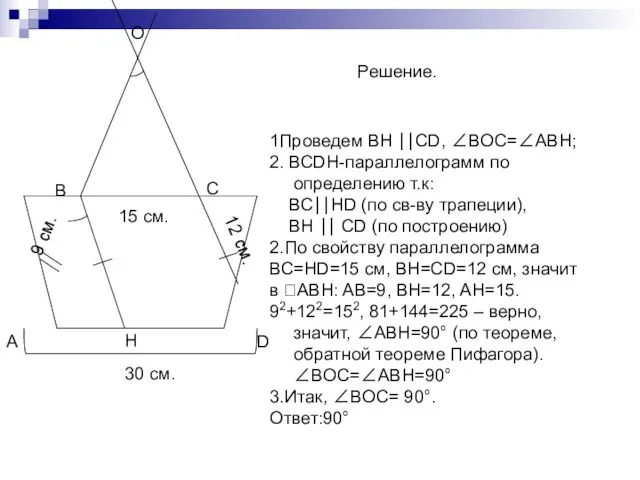
Проверка дополнительных домашних задач
Боковые стороны трапеции равны 9 см и 12 см, а основания 30 см и 15 см. Найдите угол, который образуют продолжения боковых сторон трапеции.
РЕШЕНИЕ.
(презентации учеников)

А
D
В
С
Н
О
30 см.
15 см.
12 см.
9 см.
Решение.
1Проведем BH ⎪⎪CD, ∠BOC=∠ABH;
2. ВСDН-параллелограмм по определению т.к: ВС⎪⎪НD (по св-ву трапеции),
ВН ⎪⎪ СD (по построению)
2.По свойству параллелограмма
ВС=НD=15 см, BH=CD=12 см, значит
в ABH: AB=9, BH=12, AH=15.
92+122=152, 81+144=225 – верно, значит, ∠ABH=90° (по теореме, обратной теореме Пифагора). ∠BOC=∠ABH=90°
3.Итак, ∠BOC= 90°.
Ответ:90°

Проверка дополнительных домашних задач
Точка А лежит внутри угла С, равного 60°. Расстояния от точки А до сторон этого угла a и b. Найдите:
а)расстояние от точки А до вершины С;
б)площадь четырехугольника ABCD, если AB и АD – перпендикуляры, проведенные к сторонам угла.

Точка А лежит внутри угла С, равного 60 градусам. Расстояние от точки А до сторон этого угла равны а и в. Найдите:
а) расстояние от точки А до вершины С.
в) найдите площадь 4-угольника ABCD, если AB и AD – перпендикуляры, проведённые к сторонам угла.
А
С
D
В
а)
1) Рассмотрим CED, в котором угол D=90 :
т.к. угол С равен 60 (по услов.), угол Е=90-60=30 .
Пусть СD = х, тогда СЕ = 2х (по свойству катетов в прямоугольном треугольнике). По т.П.:
Откуда .
Е
в
а
d
30
x
2x
2) Рассмотрим CDA, в котором угол D=90 :
Пусть CА =d, тогда по т. П. Откуда
Следовательно, СА= .
Ответ:
60

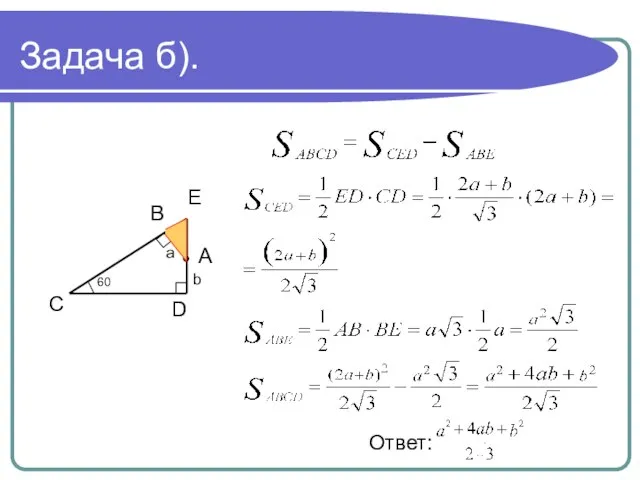
Задача б).
B
E
D
A
60
a
b
C
Ответ:

Повторяем опорные формулы
теорема Пифагора:
площадь прямоугольного треугольника:
диагональ квадрата со стороной а: катет, лежащий против угла в
теорема Пифагора:
площадь прямоугольного треугольника:
диагональ квадрата со стороной а:
катет, лежащий против угла в 30°:
площадь трапеции:

Повторяем опорные формулы
высота прямоугольного треугольника, проведенная к гипотенузе:
медиана, проведенная к гипотенузе:
катет равнобедренного треугольника с гипотенузой с:
,

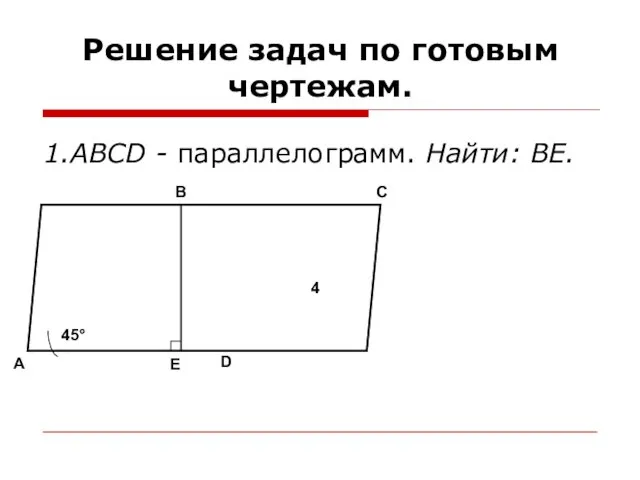
Решение задач по готовым чертежам.
1.ABCD - параллелограмм. Найти: ВЕ.
A
C
B
D
E
45°
4

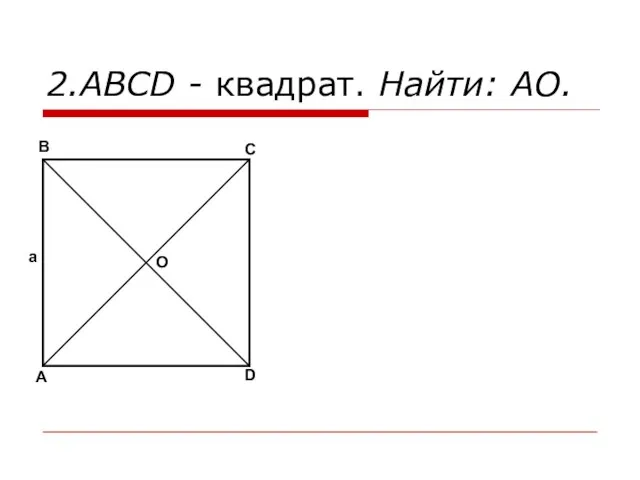
2.ABCD - квадрат. Найти: АО.
A
B
C
D
O
a

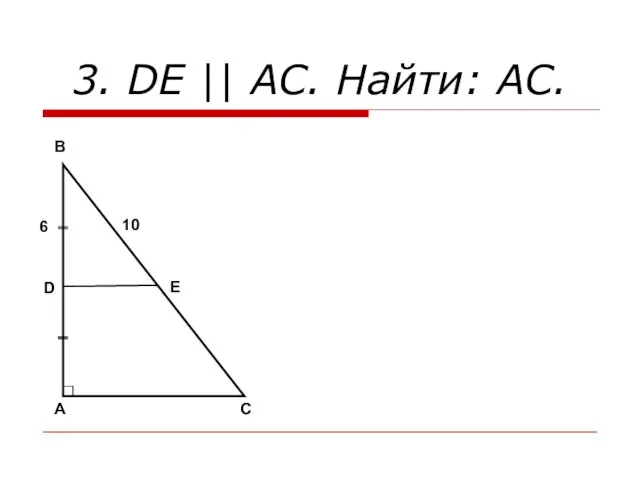
3. DE || АС. Найти: AC.
A
B
C
D
E
6
10

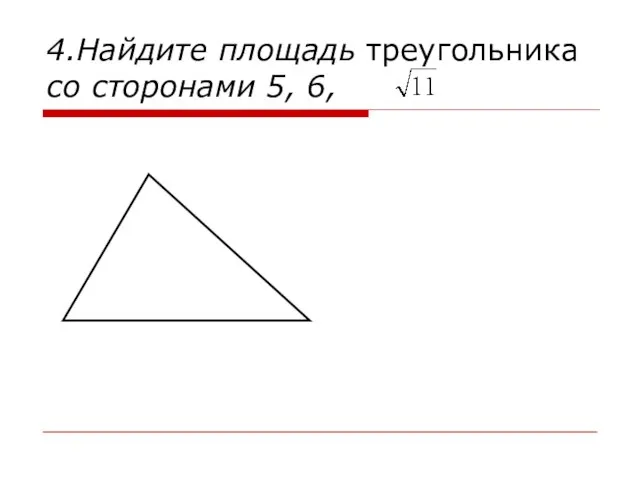
4.Найдите площадь треугольника со сторонами 5, 6,

5.ABCD - трапеция. Найти: CF.
A
B
C
D
E
F
4
30°

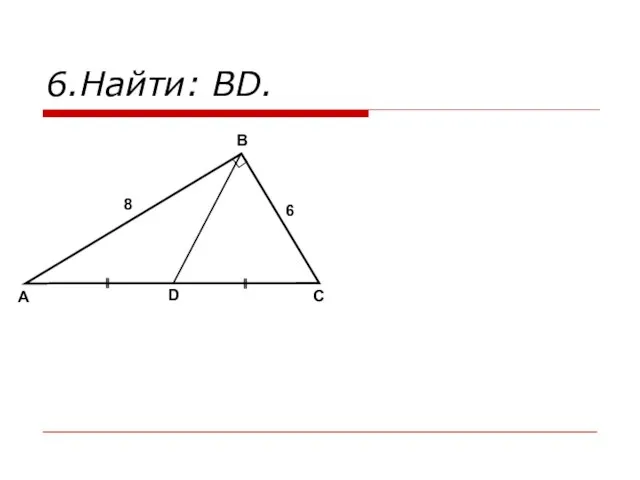
6.Найти: BD.
A
B
C
D
8
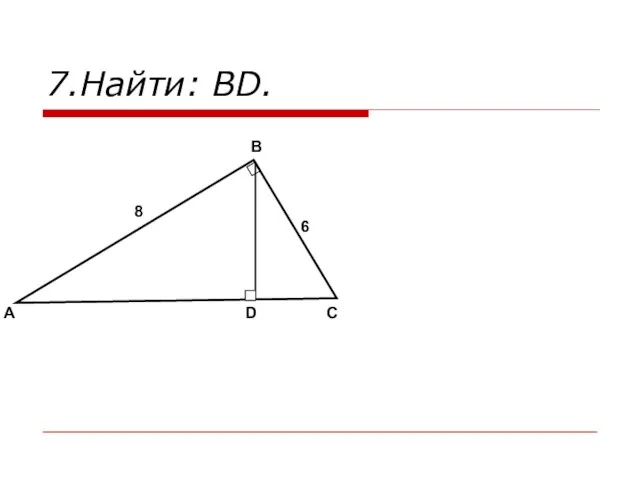
6

7.Найти: BD.
A
B
C
D
6
8

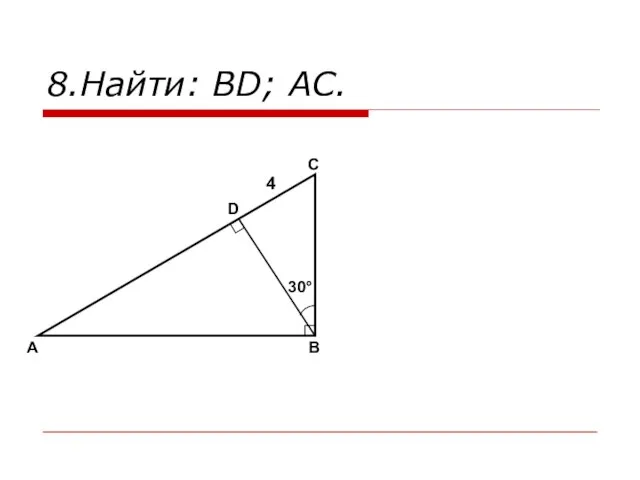
8.Найти: BD; AC.
A
B
C
D
30°
4

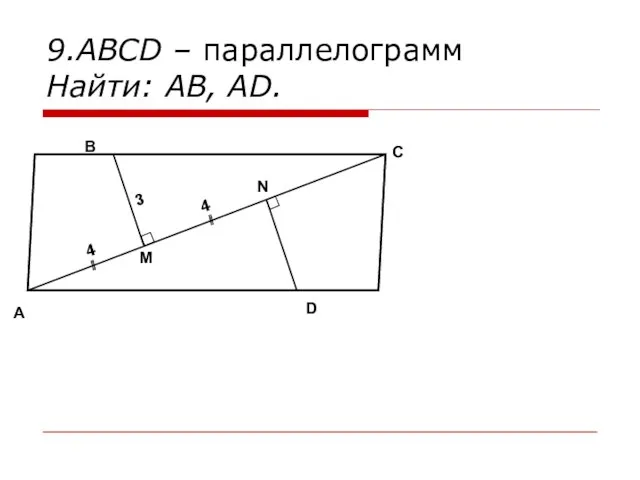
9.ABCD – параллелограмм
Найти: AB, AD.
A
B
C
D
M
N
4
4
3

Решение задач
№ 494

Боковая сторона равнобедренного треугольника равна 17 см, а биссектриса, проведенная к основанию – 15 см. Найдите площадь и периметр этого треугольника.

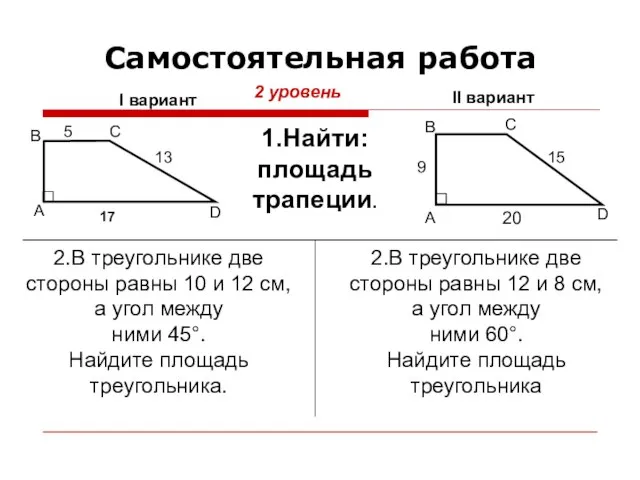
Самостоятельная работа
2 уровень
17
1.Найти: площадь трапеции.
I вариант
II вариант
20
2.В треугольнике две стороны равны 10 и 12 см, а угол между
ними 45°.
Найдите площадь треугольника.
5
13
А
B
C
D
А
B
C
D
2.В треугольнике две стороны равны 12 и 8 см, а угол между
ними 60°.
Найдите площадь треугольника
9
15