Решение задач с использованием понятия «доля»

Задачи из вариантов ЕГЭ
Определите массу воды, которую надо добавить к 20 г раствора уксусной кислоты с массовой долей 70% для получения раствора уксуса с массовой долей 3%.
Смешали 120 г раствора серной кислоты с массовой долей 20% и 40 г 50%-ного раствора того же вещества. Массовая доля кислоты в Полученном растворе равна ________% .
Какая масса азотной кислоты содержится в 1 л ее 20%-ного раствора с плотностью 1,05 г/мл?
К 120 г раствора, содержащего 80% соли, добавили 480 г раствора, содержащего 20% той же соли. Сколько процентов соли содержится в получившемся растворе?

Задачи из вариантов ЕГЭ
Кусок сплава меди с оловом массой 15 кг содержит 20% меди. Сколько чистой меди необходимо добавить к этому сплаву, чтобы новый сплав содержал 40% олова?
Первый сплав меди содержит 70 г меди, а второй сплав - 210 г серебра и 90 г меди. Взяли 225 г первого сплава и кусок второго сплава, сплавили их и получили 300 г сплава, который содержит 82% серебра. Сколько граммов серебра содержалось в первом сплаве?
В каждую из нескольких пробирок налили по две щелочи. Первую щелочь наливали по 1,2 мл в каждую пробирку. Вторую щелочь наливали по такой схеме: 0,8 мл в первую пробирку, а в каждую следующую пробирку на 0,8 мл больше, чем в предыдущую. Всего разлили 56 мл щелочей. Сколько миллилитров щелочи налили в последнюю пробирку?
Первый сплав серебра и меди содержит 430 г серебра и 70 г меди, а второй сплав - 210 г серебра и какое-то количество меди. Сплавили кусок первого сплава с куском массой 75 г второго сплава и получили 300 г сплава, который содержит 82% серебра. Определите массу (в граммах) второго сплава.

Доля
Доля - обыкновенная дробь, числитель которой равен единице.
доля – дробь (прикладные науки)
ω = 0,4

Проценты
Процент – одна сотая часть чего-либо.
Перевод доли в проценты:
0,556
0,634
0,762
Перевод процентов в доли :
34%
45,89%
23,6%

Растворы
Растворы – однородные смеси двух или большего числа веществ (компонентов).

Бесцветное вещество, без вкуса и запаха, плотность 1 г/см3, температура кипения 1000С , температура плавления (замерзания) – 00С.
Вода – единственное вещество в природе, которое в земных условиях существует в трех агрегатных состояниях: жидком, газообразном и твёрдом.

Вода – хороший растворитель. В ней растворяются твёрдые, жидкие и газообразные вещества.
Вода – хороший растворитель для многих веществ

Сплавы
Сплавы – это системы из двух или нескольких металлов (или металлов и неметаллов), обладающие по сравнению с чистыми металлами как общими металлическими, так и новыми ценными свойствами.
Количество сплавов намного больше, чем чистых металлов. Применение их разнообразно.

Сталь – сплав железа с добавками углерода, кремния и других металлов и неметаллов (до 2,5%)

Бронза – сплав меди и олова

Бронзовые предметы обихода

Дюралюминий – сплав алюминия с небольшими добавками меди, магния, марганца и кремния

Золото используется в сплавах, обычно с серебром или медью

Томпак – ”поддельное золото” – сплав меди и цинка, часто используемый для имитации золота

Латунь – сплав меди и цинка

Сплав Вуда (висмут, свинец, олово, кадмий) используется при пайке

Монель-металл (медно-никелевый сплав) используется для изготовления химического оборудования, а также в промышленности, например в паровых турбинах

Олово
Пластинки из бронзы
Медь

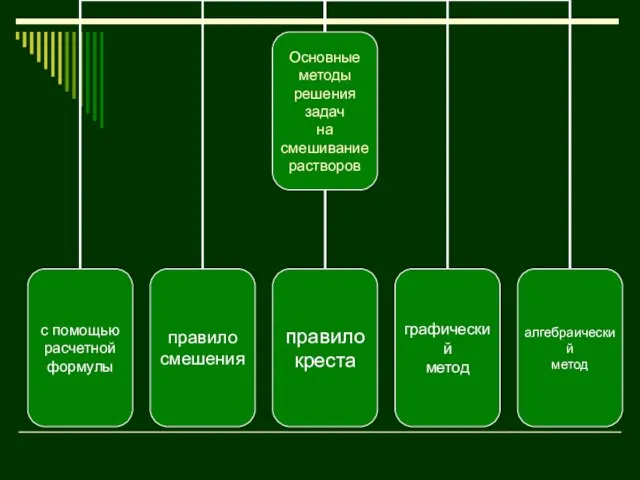
Теоретические основы решения задач

При решении задач о смесях, сплавах, растворах используют следующие допущения:
все полученные смеси, сплавы, растворы считаются однородными;
не делается различия между литром как мерой вместимости сосуда и литром как мерой количества жидкости (или газа);
смешивание различных растворов происходит мгновенно;
объем смеси равен сумме объемов смешиваемых растворов;
объемы растворов и массы сплавов не могут быть отрицательными.

Определения и обозначения
Массовая доля растворенного вещества в растворе - это отношение массы этого вещества к массе раствора.
где ω(в-ва) - массовая доля растворенного вещества в растворе;
m(в-ва) - масса растворенного вещества в растворе;
m(р-ра) - масса раствора.

Определения и обозначения
Введем обозначения:
ω1(в-ва) - массовая доля растворенного вещества в первом растворе;
ω2(в-ва) - массовая доля растворенного вещества во втором растворе;
ω(в-ва) - массовая доля растворенного вещества в новом растворе, полученном при смешивании первого и второго растворов;
m1(в-ва), m2(в-ва), m(в-ва) – массы растворенных веществ в соответствующих растворах;
m1(р-ра), m2(р-ра), m(р-ра) - массы соответствующих растворов.

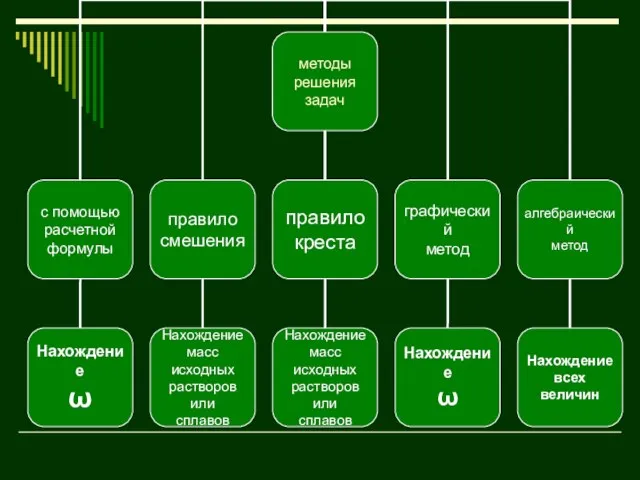
С помощью расчетной формулы
Масса полученного при смешивании раствора равна:
т(р-ра) = т1(р-ра) + т2(р-ра)
массы растворенных веществ в первом и втором растворах:
т1(в-ва) = ω1(в-ва)·т1(р-ра),
т2(в-ва) = ω2(в-ва)·т2(р-ра)
масса растворенного вещества в полученном растворе вычисляется как сумма масс веществ в исходных раствopax:
т(в-ва) = m1(в-ва) + т2(в-ва) = ω1(в-ва)·т1(р-ра) + ω2(в-ва)·т2(р-ра)

С помощью расчетной формулы
Таким образом, массовая доля растворенного вещества в
полученном растворе равна:

«Правило смешения»
Исходя из формулы:

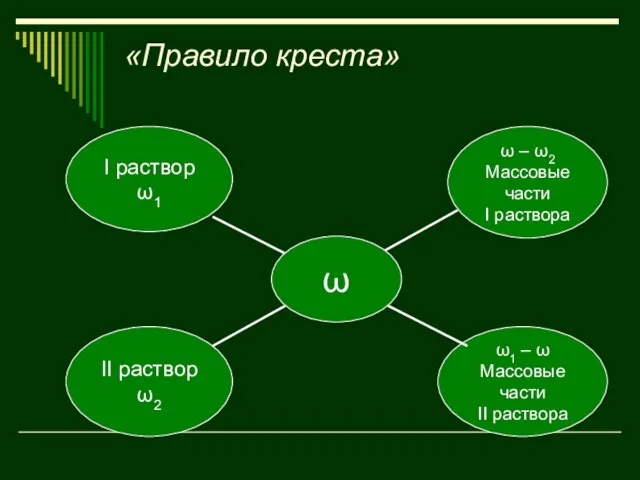
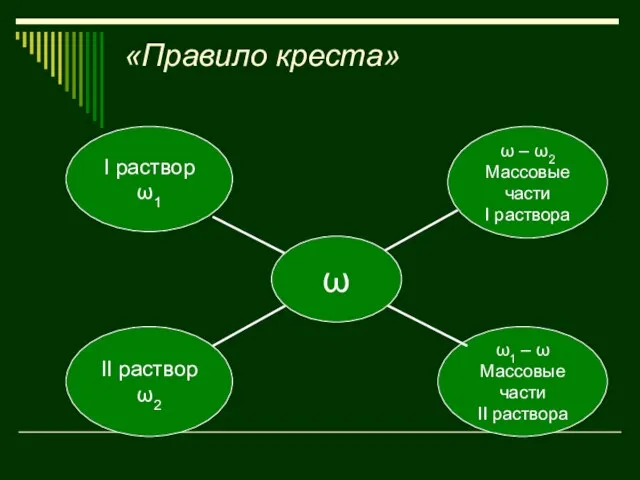
«Правило креста»

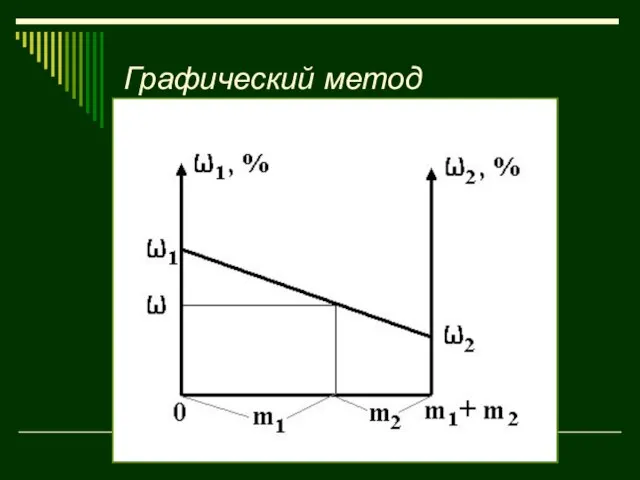
Грaфuческий метод

Алгебраический метод
Задачи на смешивание растворов решают с помощью составления уравнения или системы уравнений.

Решение задач
Приготовление растворов или сплавов
В воде массой 400 г растворили 50 г серной кислоты. Какова массовая для серной кислоты в полученном растворе?
Найти массу воды и соли, необходимых для приготовления 500 г 25%-ного раствора этой соли.
Сплавили 60 г серебра и 240 г меди. Найти массовую долю серебра в полученном сплаве.

Решение задач
Приготовление растворов или сплавов
Какую массу алюминия и магния необходимо взять, чтобы приготовить образец сплава массой 300 г, содержащий 45% алюминия?
Массовая доля солей в морской воде достигает 3,5%. Определите массу соли, остающейся после выпаривания морской воды объемом 8,93 л с плотностью 1,12 г/мл.
Какая масса карбоната натрия потребуется для приготовления 0,5 л 13%-ного раствора плотностью 1,13 г/мл?

Решение задач
Сложные проценты
Задача 1
К 100 г 20%-ного раствора соли добавили 300 г её 10%-ного раствора. Определите процентную концентрацию полученного раствора.

Решение
Алгебраический метод
m1(р-ра) = 100 г
m2(р-ра) = 300 г
ω1(в-ва) = 0,2
ω2(в-ва) = 0,1
ω(в-ва) - ?
Первый раствор:
m1(р-ра) = 100 г, m1(в-ва) = 100.0,2 = 20 (г)
Второй раствор :
m2(р-ра) = 300 г, m2(в-ва) = 300.0,1 = 30 (г)
Полученный раствор :
m(р-ра) = 100 + 300 = 400 (г), m(в-ва) = 20 + 30 =50 (г)
Тогда,
Ответ: 12,5%.

Решение
С помощью расчетной формулы
m1(р-ра) = 100 г
m2(р-ра) = 300 г
ω1(в-ва) = 0,2
ω2(в-ва) = 0,1
ω(в-ва) - ?
Используем формулу:
Получаем:
Ответ: 12,5%

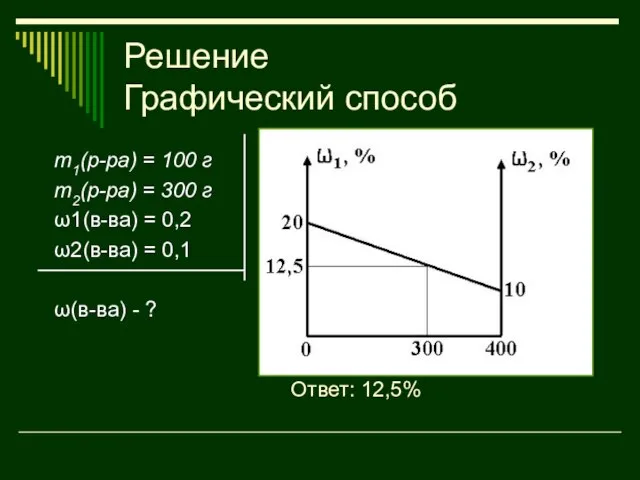
Решение
Графический способ
m1(р-ра) = 100 г
m2(р-ра) = 300 г
ω1(в-ва) = 0,2
ω2(в-ва) = 0,1
ω(в-ва) - ?
Ответ: 12,5%

Решение задач
Сложные проценты
Задача 2
Смешали 10%-ный и 25%-ный растворы соли и получили 3 кг 20%-ного раствора. Какое количество каждого раствора в килограммах было использовано?

Решение
Алгебраический метод
ω1(в-ва) = 0,1
ω2(в-ва) = 0,25
m(р-ра) = 3 кг
ω(в-ва) = 0,2
m1(р-ра) - ?
m2(р-ра) - ?
Первый раствор:
m1(р-ра) = x кг, m1(в-ва) = 0,1.x (кг)
Второй раствор :
m2(р-ра) = (3 – x) кг, m2(в-ва) = (0,25.(3 – x)) кг
Полученный раствор :
m(р-ра) = 3 кг, m(в-ва) = 3.0,2 = 0,6 (кг)
Так как масса вещества в полученном растворе
0,6 кг, можно составить уравнение:
0,1x + 0,25(3 - x) =0,6
0,1x + 0,75 – 0,25x =0,6
0,1x – 0,25x =0,6 - 0,75
- 0,15x = - 0,15
X=1
Масса первого раствора 1 кг, масса второго раствора 3 -1 = 2 (кг)
Ответ: 1 кг, 2 кг.

Решение
Графический способ
ω1(в-ва) = 0,1
ω2(в-ва) = 0,25
m(р-ра) = 3 кг
ω(в-ва) = 0,2
m1(р-ра) - ?
m2(р-ра) - ?
Ответ: 1 кг, 2 кг.

Решение
«Правило смешения»
ω1(в-ва) = 0,1
ω2(в-ва) = 0,25
m(р-ра) = 3 кг
ω(в-ва) = 0,2
m1(р-ра) - ?
m2(р-ра) - ?
Воспользуемся формулой:
Получаем:
m1 = 0,5m2
m1 + m2 = 3, следовательно, m1 = 1 кг, m2 = 2 кг.
Ответ: 1 кг, 2 кг.

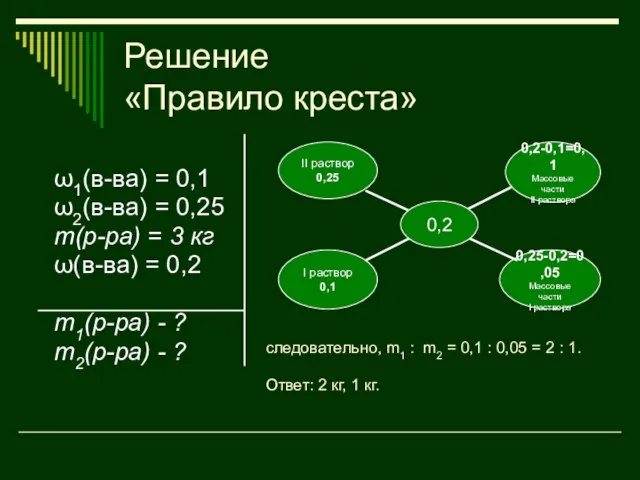
Решение
«Правило креста»
ω1(в-ва) = 0,1
ω2(в-ва) = 0,25
m(р-ра) = 3 кг
ω(в-ва) = 0,2
m1(р-ра) - ?
m2(р-ра) - ?
следовательно, m1 : m2 = 0,1 : 0,05 = 2 : 1.
Ответ: 2 кг, 1 кг.

Решение задач
Сложные проценты
К 300 г раствора, содержащего 10% соли, добавили некоторое количество раствора, содержащего 30% той же соли. Получили раствор, содержащий 15% соли. Какую массу второго раствора взяли?
Имеются два слитка сплава серебра и олова. Первый слиток содержит 360 г серебра и 40 г олова, а второй слиток - 450 г серебра и 150 г олова. От каждого слитка взяли по куску, сплавили их и получили 200 г сплава, в котором оказалось 81 % серебра. Определите массу (в граммах) куска, взятого от второго слитка.

«Правило креста»

Решение задач
Сложные проценты
Имеется сталь двух сортов с содержанием никеля 5% и 40%. Сколько тонн стали первого сорта нужно взять, чтобы в смеси со вторым сортом получить при плавке 140 т стали с содержанием никеля 30%?
Имеются два сплава, в первом из которых содержится 40%, а во втором - 20% серебра. Сколько килограммов второго сплава необходимо добавить к 20 кг первого сплава, чтобы получить сплав, содержащий 30% серебра?
Проверить
Дальше

Решение
Алгебраический метод
m1(сп-ва) = 20 кг
ω1(Ag) = 0,4
ω2(Ag) = 0,2
ω(Ag) = 0,3
m2(сп-ва) - ?
Первый сплав:
m1(сп-ва) = 20 кг, m1(Ag) = 20.0,4 = 8 (кг)
Второй сплав:
m2(сп-ва) = x кг, m2(Ag) = (x.0,2) кг
Полученный сплав:
m(сп-ва) = (20 + x) кг, m(Ag) = (8 + 0,2x) кг
Так как ω(Ag) = 0,3, то
8 + 0,2x = 6 + 0,3x
0,2x – 0,3x = 6 - 8
-0,1x = -2
x=20
Ответ: 20 кг.

Решение
«Правило смешения»
m1(сп-ва) = 20 кг
ω1(Ag) = 0,4
ω2(Ag) = 0,2
ω(Ag) = 0,3
m2(сп-ва) - ?
Воспользуемся формулой:
Получаем:
m1 = m2 = 20 кг.
Ответ: 20 кг.

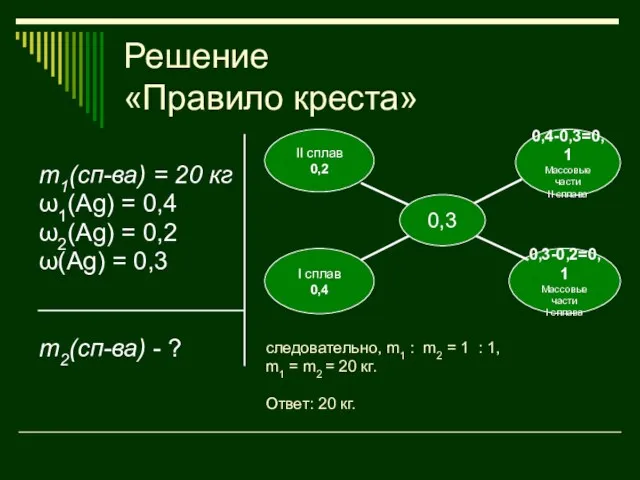
Решение
«Правило креста»
m1(сп-ва) = 20 кг
ω1(Ag) = 0,4
ω2(Ag) = 0,2
ω(Ag) = 0,3
m2(сп-ва) - ?
следовательно, m1 : m2 = 1 : 1,
m1 = m2 = 20 кг.
Ответ: 20 кг.

Решение задач
Сложные проценты
Имеются два слитка сплава золота с медью. Первый слиток содержит 230 г золота и 20 г меди, а второй слиток - 240 г золота и 60 г меди. От каждого слитка взяли по куску, сплавили их и получили 300 г сплава, в котором оказалось 84% золота. Определите массу (в граммах) куска, взятого от первого слитка.
К 120 г раствора, содержащего 80% соли, добавили 480 г раствора, содержащего 20% той же соли. Сколько процентов соли содержится в получившемся растворе.