Урок на тему : «Исследование функции с помощью производной»с использованием компьютерных технологийУчитель математики Бахт
Содержание
- 2. Исследование функций и построение графиков с помощью производной
- 3. «…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…» Н.И.
- 4. Цели урока: ⮚ Образовательные. Формировать: - навыки прикладного использования аппарата производной; - выявить уровень овладения учащимися
- 5. I этап. Актуализация ЗУН, необходимых для творческого применения знаний Необходимое условие возрастания и убывания функции Достаточное
- 6. Необходимое условие возрастания и убывания функции Т е о р е м а. Если дифференцируемая функция
- 7. Достаточные условия возрастания и убывания функции Теорема Лагранжа. Если функция f(x), х∈[а;b], непрерывна на отрезке [а;b]
- 8. Достаточное условие возрастания функции Теорема. Если функция f имеет неотрицательную производную в каждой точке интервала (а;b),
- 9. Достаточное условие убывания функции Теорема. Если функция имеет неположительную производную в каждой точке интервала (а;b), то
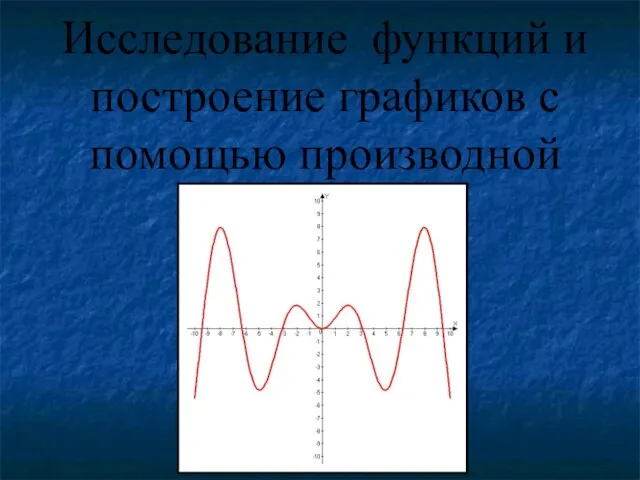
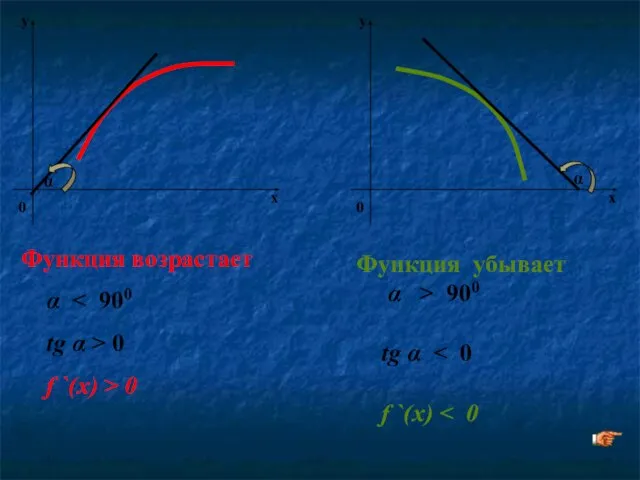
- 10. α α Функция возрастает α tg α > 0 f `(x) > 0 Функция убывает α
- 11. Правило нахождения интервалов монотонности 1) Вычисляем производную f `(x) данной функции f(x), а затем находим точки,
- 12. Правило нахождения интервалов монотонности 2) Критическими точками область определения функции f(x) разбивается на интервалы, на каждом
- 13. Правило нахождения интервалов монотонности 3) Определим знак f `(x) на каждом из найденных интервалов. Если на
- 14. Исследование экстремумов функции Необходимое условие экстремума. (теорема Ферма) Если точка х0 является точкой экстремума функции f
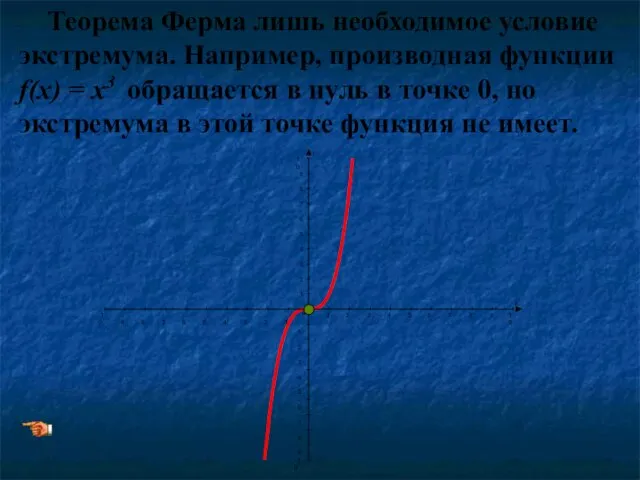
- 15. Теорема Ферма лишь необходимое условие экстремума. Например, производная функции f(x) = x3 обращается в нуль в
- 16. Достаточные условия существования экстремума в точке Признак максимума функции. Если функция f непрерывна в точке х0,
- 17. Достаточные условия существования экстремума в точке Признак минимума функции. Если функция f непрерывна в точке х0,
- 18. Достаточные условия выпуклости и вогнутости графика функции Т е о р е м а. Пусть функция
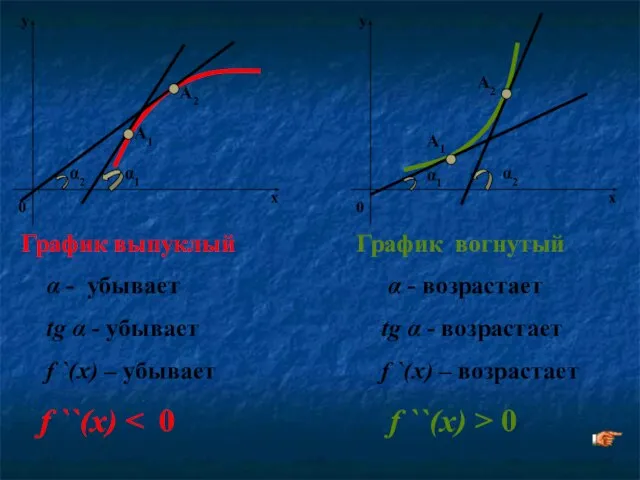
- 19. α1 α2 График выпуклый α - убывает tg α - убывает f `(x) – убывает f
- 20. Точки перегиба Найти критические точки функции по второй производной. Исследовать знак второй производной в некоторой окрестности
- 21. Заполните таблицу Задание для всех учащихся. II этап. Обобщение и систематизация знаний и способов деятельности
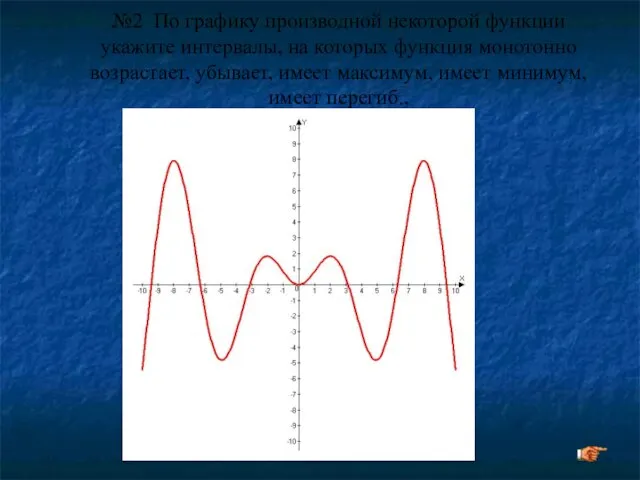
- 23. №2 По графику производной некоторой функции укажите интервалы, на которых функция монотонно возрастает, убывает, имеет максимум,
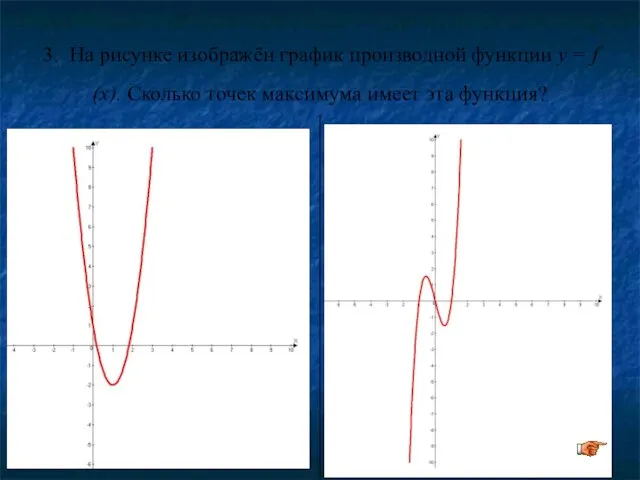
- 24. 3. На рисунке изображён график производной функции y = f (x). Сколько точек максимума имеет эта
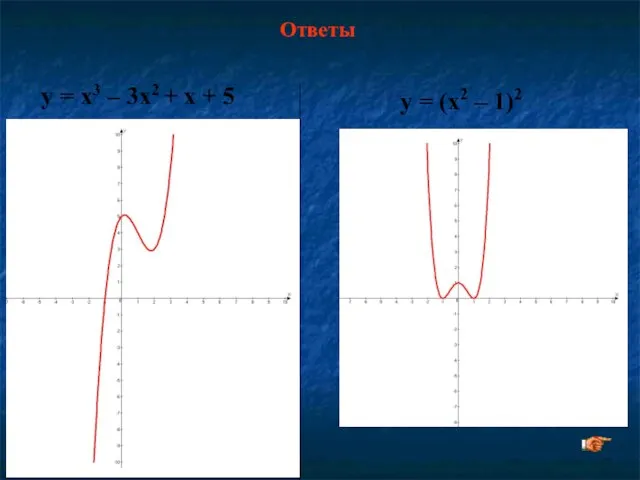
- 25. у = x3 – 3x2 + x + 5 у = (x2 – 1)2 Ответы
- 26. III этап. Усвоение образца комплексного применения ЗУН.
- 28. Исследовать функцию на выпуклость, вогнутость.
- 29. Мини - исследовательская работа Выбери задание 1. 3. 5. 2. 4. 6.
- 30. Тест Кроссворд
- 32. Скачать презентацию




![Достаточные условия возрастания и убывания функции Теорема Лагранжа. Если функция f(x), х∈[а;b],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/429755/slide-6.jpg)














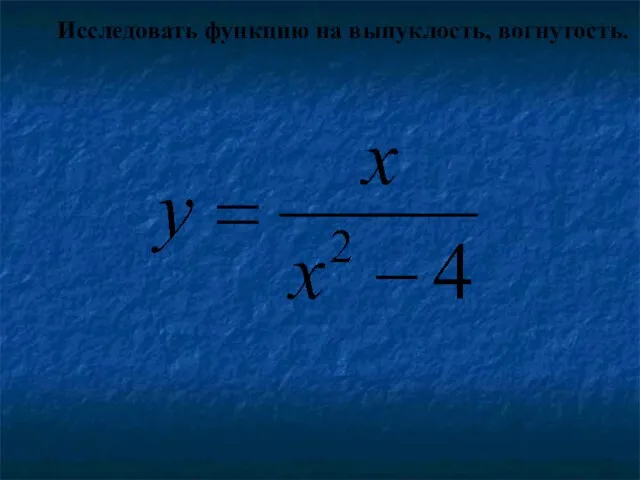


 Особенности истории России. Место России в мировом историческом процессе
Особенности истории России. Место России в мировом историческом процессе Оппортунистические инфекции
Оппортунистические инфекции  Всемирный день борьбы со СПИДом
Всемирный день борьбы со СПИДом Доказательная медицина и стандарты медицинской деятельности
Доказательная медицина и стандарты медицинской деятельности Система счетов и двойная запись
Система счетов и двойная запись Презентация на тему Лепка из пластилина
Презентация на тему Лепка из пластилина  Ночевала тучка золотая
Ночевала тучка золотая Revision
Revision Материально-производственная деятельность человека.
Материально-производственная деятельность человека. Как помочь ребёнку быть внимательным.
Как помочь ребёнку быть внимательным. Защитники земли русской. Работы учеников
Защитники земли русской. Работы учеников Презентация на тему ПОЛИТИЧЕСКИЙ ПРОГНОЗ: сущность, научные основы и принципы
Презентация на тему ПОЛИТИЧЕСКИЙ ПРОГНОЗ: сущность, научные основы и принципы  Словообразование (6 класс)
Словообразование (6 класс) 1 сентября. Классный час «От пера до компьютера».
1 сентября. Классный час «От пера до компьютера». Грамматические особенности перевода арабских фильмов на русский язык
Грамматические особенности перевода арабских фильмов на русский язык 1.3.2 Логические элементы ЭВМ
1.3.2 Логические элементы ЭВМ HTML
HTML Психологический климат в трудовом коллективе
Психологический климат в трудовом коллективе НОУ СОШ Гармония
НОУ СОШ Гармония Китайско-конфуцианская цивилизация
Китайско-конфуцианская цивилизация Каракули. Упражнение 2
Каракули. Упражнение 2 Презентация на тему Треугольники 7 класс геометрия
Презентация на тему Треугольники 7 класс геометрия  Moral Crisis in south Africa
Moral Crisis in south Africa Промоагентство
Промоагентство Презентация на тему Проблема темперамента и характера
Презентация на тему Проблема темперамента и характера Мой творческий путь в прозе и стихах
Мой творческий путь в прозе и стихах ПРОГРАММА«ТРИ ШАГА К УНИКАЛЬНОМУ СЕРВИСУ»GLOBAL SOLUTIONS Ltd.
ПРОГРАММА«ТРИ ШАГА К УНИКАЛЬНОМУ СЕРВИСУ»GLOBAL SOLUTIONS Ltd. Политические режимы. Типы политических режимов
Политические режимы. Типы политических режимов