Содержание
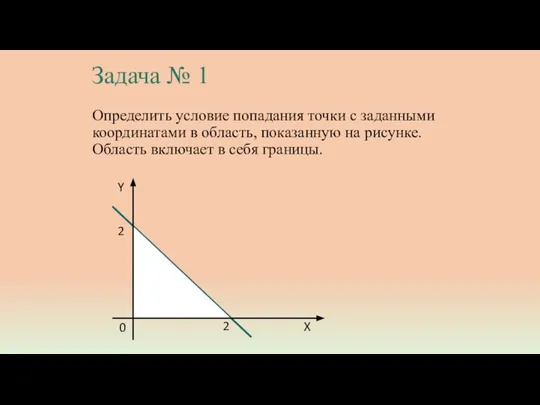
- 2. Задача № 1 Определить условие попадания точки с заданными координатами в область, показанную на рисунке. Область
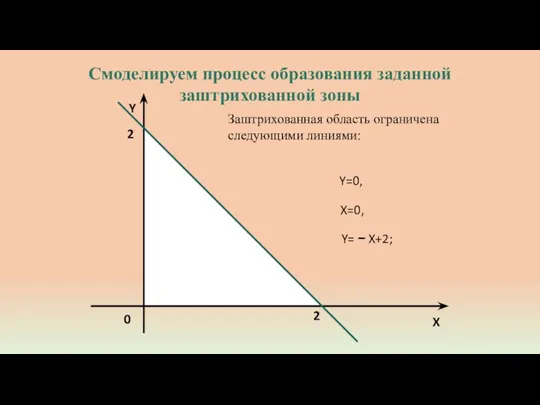
- 3. Y 2 0 X 2 Заштрихованная область ограничена следующими линиями: X=0, Y= − X+2; Y=0, Смоделируем
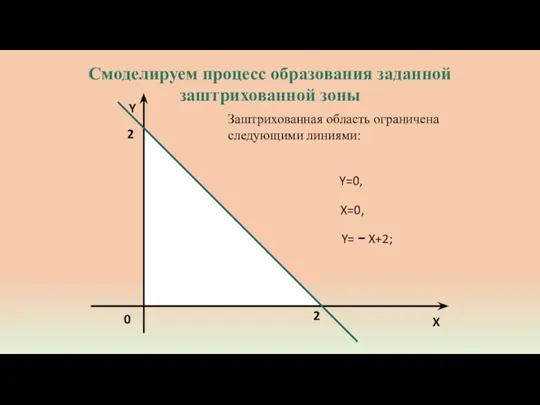
- 4. Y 2 0 X 2 Заштрихованная область ограничена следующими линиями: X=0, Y= − X+2; Y=0, Смоделируем
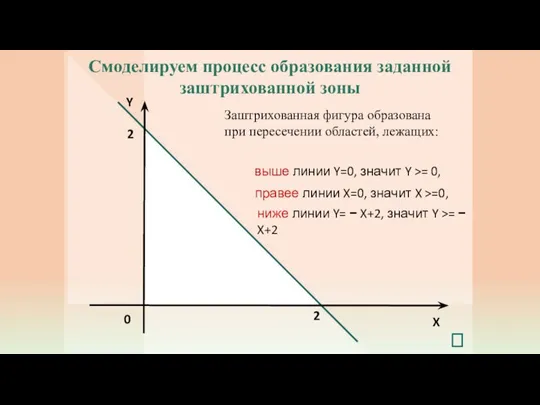
- 5. Y 2 0 X 2 Смоделируем процесс образования заданной заштрихованной зоны Заштрихованная фигура образована при пересечении
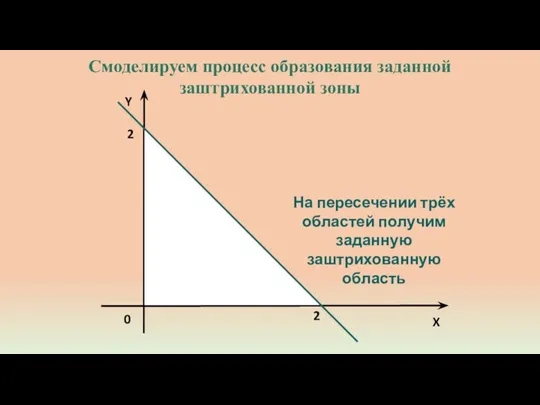
- 6. Y 2 0 X 2 На пересечении трёх областей получим заданную заштрихованную область Смоделируем процесс образования
- 7. Сформулируем условие принадлежности точки данной заштрихованной области Т.к. границы принадлежат заштрихованной зоне, то условия будут нестрогими
- 8. Опишем условие попадания точки в область на языке Pascal ….. If (X >= 0) and (Y
- 9. Например: Дана точка с координатами (1,1); Проверка: (1 > 0) and (1 > 0) and (1
- 10. Например: Дана точка с координатами (1.5, 2); Проверка: (1.5 >= 0) and (2 >= 0) and
- 11. Задача № 2 Определить условие попадания точки с заданными координатами в область, показанную на рисунке. Область
- 12. Заштрихованная область состоит из двух частей, которые ограничены следующими линиями: Смоделируем процесс образования заданной заштрихованной зоны
- 13. 4 0 Y X 4 Процесс образования первой области мы рассмотрели в предыдущей задаче ? Вторая
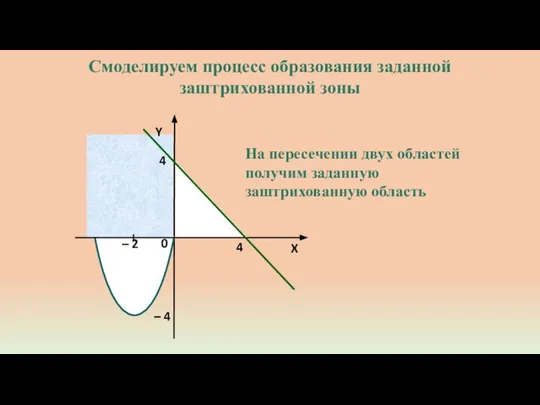
- 14. На пересечении двух областей получим заданную заштрихованную область Смоделируем процесс образования заданной заштрихованной зоны
- 15. Сформулируем условие принадлежности точки данной заштрихованной области Т.к. границы принадлежат заштрихованной зоне, то условия будут нестрогими
- 16. Опишем условие попадания точки в область на языке Pascal ….. If (Y >= 0) and (X
- 17. Например: Дана точка с координатами (- 2, -1); Проверка: (- 2 >= 0) and (-1 >=
- 18. Задача № 3 (самостоятельно) Определить условие попадания точки с заданными координатами в область, показанную на рисунке.
- 20. Скачать презентацию











 Вклад М.В.Ломоносова в русскую литературу
Вклад М.В.Ломоносова в русскую литературу Создание дидактических материалов по истории с использованием средств ИКТ к теме «Занимательная история»
Создание дидактических материалов по истории с использованием средств ИКТ к теме «Занимательная история» О проведении работы по медицинскому обеспечению летней оздоровительной кампании 2012 года в Пермском крае
О проведении работы по медицинскому обеспечению летней оздоровительной кампании 2012 года в Пермском крае Higher education traditions in the USA
Higher education traditions in the USA Великий ученый - энциклопедист
Великий ученый - энциклопедист Типы текста
Типы текста Строим пирамиду
Строим пирамиду Основные элементы оборудования и наполнения среды
Основные элементы оборудования и наполнения среды Презентация на тему Понятие, этапы развития и функции денег
Презентация на тему Понятие, этапы развития и функции денег Оптические иллюзии в живописи и графике
Оптические иллюзии в живописи и графике Культура и общество
Культура и общество Д.Поллок
Д.Поллок BLANCOSUBLINEДизайнерское решение для подстольного монтажа – семейство моек BlancoSubline из Silgranit® CLEAN
BLANCOSUBLINEДизайнерское решение для подстольного монтажа – семейство моек BlancoSubline из Silgranit® CLEAN Топливно-энергетический комплекс мира (ТЭК)
Топливно-энергетический комплекс мира (ТЭК)  Экспериментальная установка теплового насоса
Экспериментальная установка теплового насоса 드라마와 함께 하는 한국어 수 업제2 강강
드라마와 함께 하는 한국어 수 업제2 강강 Сравнение умственной работоспособности обучающихся младшей и старшей школы в стрессовой ситуации
Сравнение умственной работоспособности обучающихся младшей и старшей школы в стрессовой ситуации Условия для реализации основной образовательной программы ДО.
Условия для реализации основной образовательной программы ДО. Школьною тропинкой начинается Жизнь, поверь, у каждого из нас. И о чём мечтали, всё сбывается! Переходим мы из класса в класс…
Школьною тропинкой начинается Жизнь, поверь, у каждого из нас. И о чём мечтали, всё сбывается! Переходим мы из класса в класс…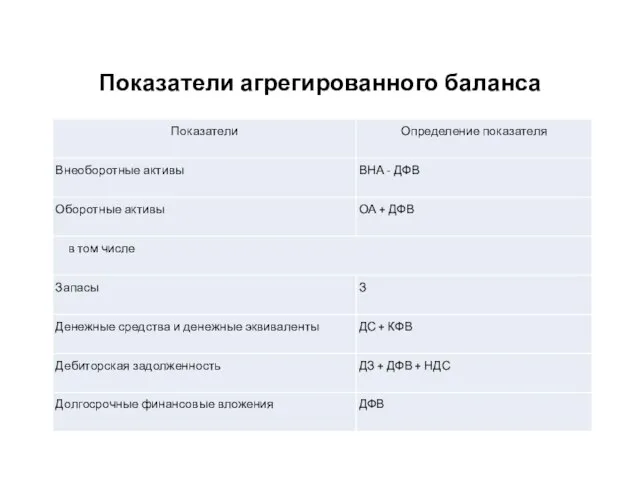 Показатели агрегированного баланса
Показатели агрегированного баланса Сложное предложение (4 класс)
Сложное предложение (4 класс) Презентация Киренский 2022
Презентация Киренский 2022 Самоконтроль в обучении
Самоконтроль в обучении Результаты выполнения Росприроднадзором поручений Минприроды России по подготовке плана по реализации комплекса мер, направленн
Результаты выполнения Росприроднадзором поручений Минприроды России по подготовке плана по реализации комплекса мер, направленн Единственное право и единственная обязанность силы – это защищать слабого Волкодав
Единственное право и единственная обязанность силы – это защищать слабого Волкодав Презентация на тему Древний Вавилон
Презентация на тему Древний Вавилон Школа Панацея 03.09.2020
Школа Панацея 03.09.2020 EUGR NSP CLUB Лекция 3 OMEGA-3 Обзор партнёра компании NSP спортивного врача И.И.Шашкова.
EUGR NSP CLUB Лекция 3 OMEGA-3 Обзор партнёра компании NSP спортивного врача И.И.Шашкова.