Содержание
- 2. Урок геометрии в 8 классе Тема: Теорема о серединном перпендикуляре Цели: ввести понятие серединного перпендикуляра к
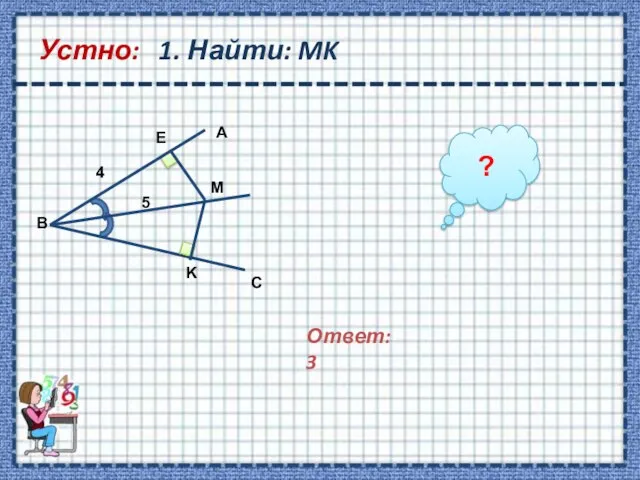
- 3. Устно: 1. Найти: MK Ответ: 3 ?
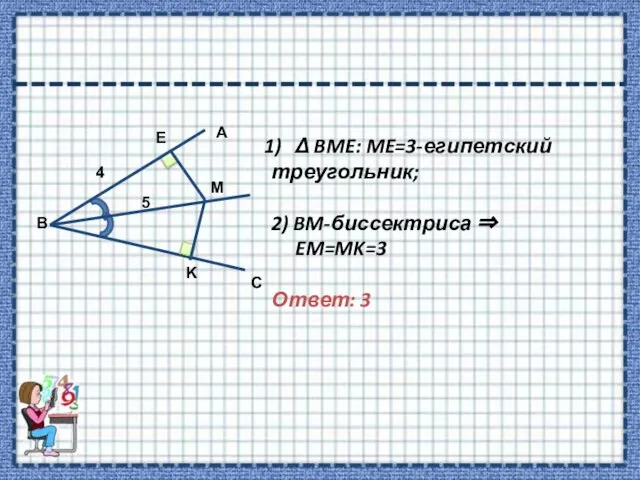
- 4. Δ BME: ME=3-египетский треугольник; 2) BM-биссектриса EM=MK=3 Ответ: 3
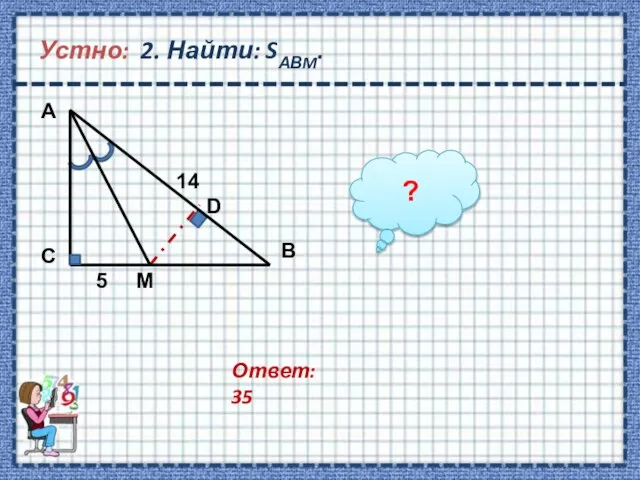
- 5. Устно: 2. Найти: SАВM. Ответ: 35 ?
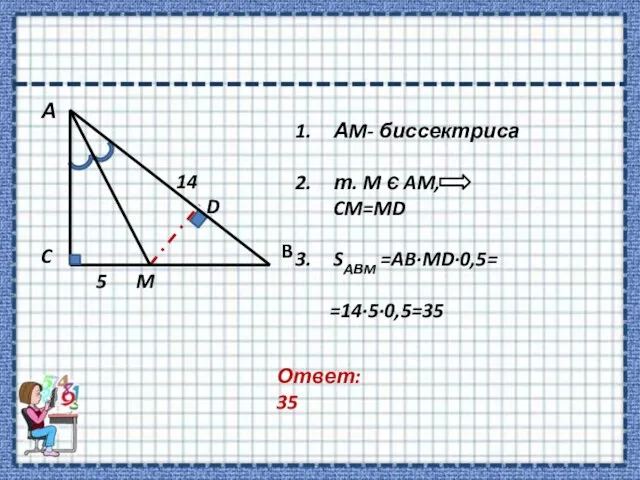
- 6. Ответ: 35
- 7. Геометрия - удивительная наука. Её история насчитывает не одно тысячелетие, но каждая встреча с ней способна
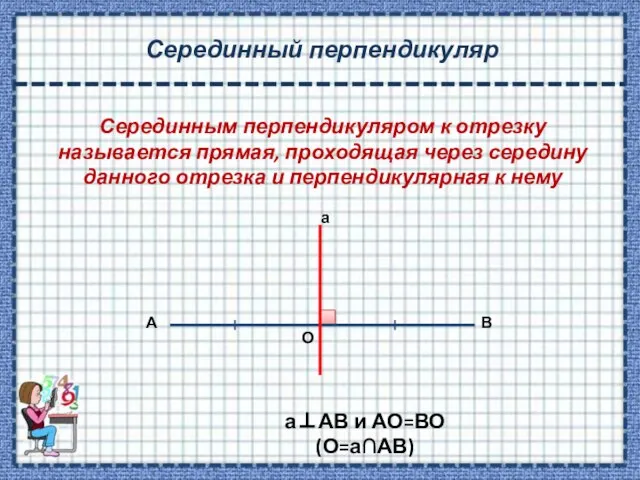
- 8. Серединный перпендикуляр Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к
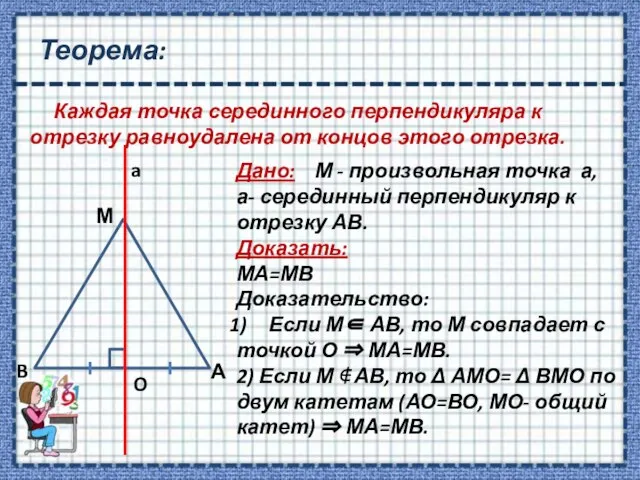
- 9. Теорема: Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Дано: М - произвольная
- 10. Обратно: Каждая точка, равноудаленная от концов этого отрезка, лежит на серединном перпендикуляре к нему. Дано: NА=NВ,
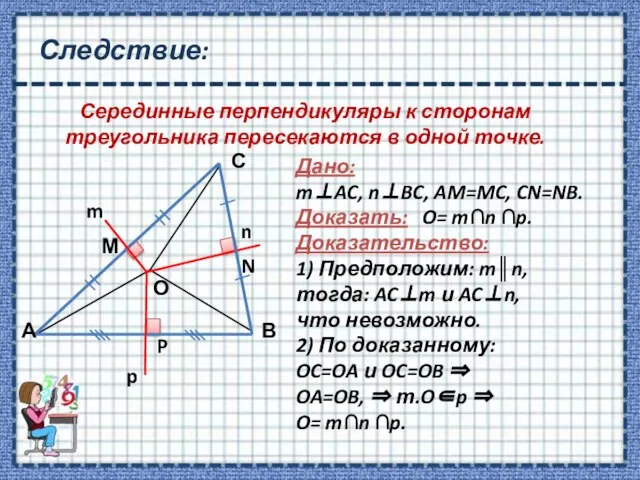
- 11. Следствие: Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Дано: mAC, nBC, AM=MC, CN=NB. Доказать:
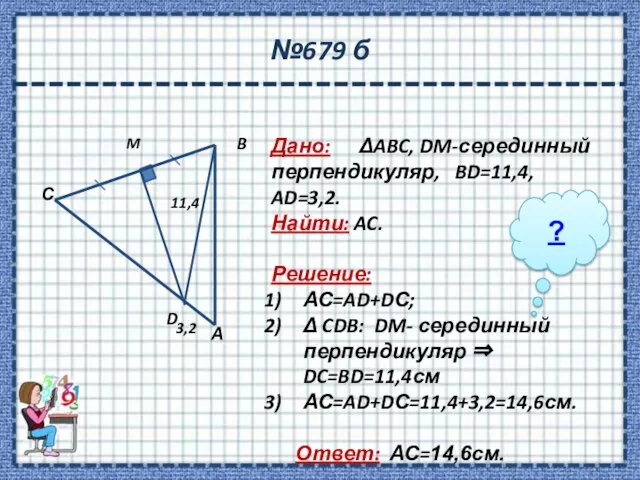
- 12. №679 б Дано: ΔABC, DM-серединный перпендикуляр, BD=11,4, AD=3,2. Найти: AC. Решение: АС=AD+DС; Δ CDB: DM- серединный
- 13. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
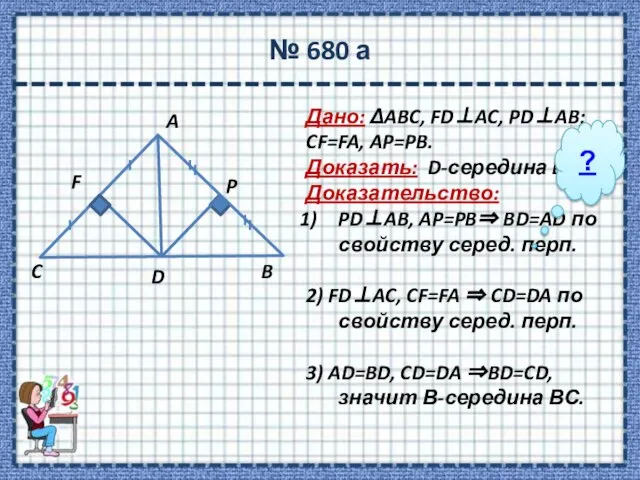
- 14. № 680 а Дано: ΔABC, FDAC, PDAB; CF=FA, AP=PB. Доказать: D-середина BC. Доказательство: PDAB, AP=PB BD=AD
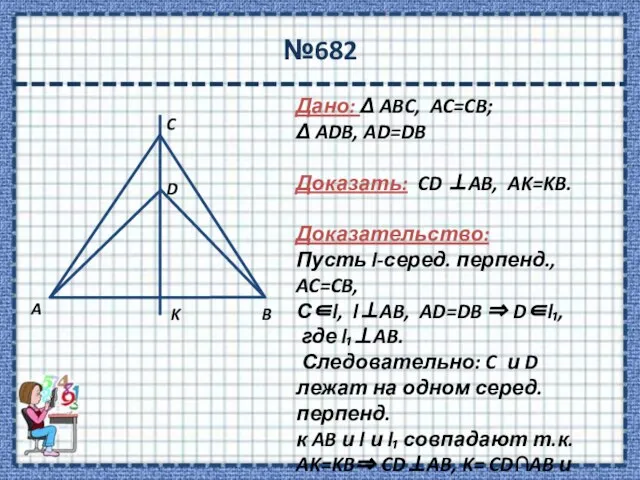
- 15. №682 Дано: Δ ABC, AC=CB; Δ ADB, AD=DB Доказать: CD AB, AK=KB. Доказательство: Пусть l-серед. перпенд.,
- 16. Оцените свою деятельность по пятибалльной шкале: Устные задачи- Работа у доски – Работа на месте –
- 17. Атанасян Л.С. и др. Геометрия 7-9 классы. – М:, Просвещение, 2008г. 2. Атанасян Л.С., Бутузов В.Ф.
- 19. Скачать презентацию






 Взрослая жизнь взрослая ответственность
Взрослая жизнь взрослая ответственность Презентация на тему Понятие дроби. Равенство дробей
Презентация на тему Понятие дроби. Равенство дробей  Головка для расчистки Mense RP 80
Головка для расчистки Mense RP 80 한국 음식들
한국 음식들 Тихвинская ярмарка – 2006 п. Подосиновец
Тихвинская ярмарка – 2006 п. Подосиновец Токарные инструменты
Токарные инструменты ПАКЕТ ПРИКЛАДНЫХ ПРОГРАММ БАЗИС
ПАКЕТ ПРИКЛАДНЫХ ПРОГРАММ БАЗИС Методические пособия и литература по предмету
Методические пособия и литература по предмету Big ben
Big ben Choosing independent variables
Choosing independent variables Презентация на тему Жизнь древних славян
Презентация на тему Жизнь древних славян  Логические схемы алгоритмов
Логические схемы алгоритмов  Университет и сообщество: 3 этапметодический семинар
Университет и сообщество: 3 этапметодический семинар Онлайн-подготовка к ЕГЭ
Онлайн-подготовка к ЕГЭ Планирование подготовки к городскому этапу соревнований в Севастополе на 6 месяцев (с 1 декабря 2020 г по 31 мая 2021 г.)
Планирование подготовки к городскому этапу соревнований в Севастополе на 6 месяцев (с 1 декабря 2020 г по 31 мая 2021 г.) Успех деловых переговоров
Успех деловых переговоров Золотые руки
Золотые руки ВКР
ВКР Эволюционное развитие налогообложения
Эволюционное развитие налогообложения Особенности раннего творчества О.Э.Мандельштама
Особенности раннего творчества О.Э.Мандельштама Бизнес-планирование. Литература (основная)
Бизнес-планирование. Литература (основная) Определение искривлений позвоночника
Определение искривлений позвоночника Устройство для разделения нефтесодержащих жидкостей
Устройство для разделения нефтесодержащих жидкостей Презентация на тему Вооруженные силы РФ
Презентация на тему Вооруженные силы РФ Презентация на тему Деление
Презентация на тему Деление «Реабилитация бизнеса»
«Реабилитация бизнеса» Тема собрания: «Конфликтные ситуации учитель - родитель»
Тема собрания: «Конфликтные ситуации учитель - родитель» МИССИЯ ООО «БукЪвица»
МИССИЯ ООО «БукЪвица»