Содержание
- 2. The formulas we have developed so far allow us to compute the present or future value
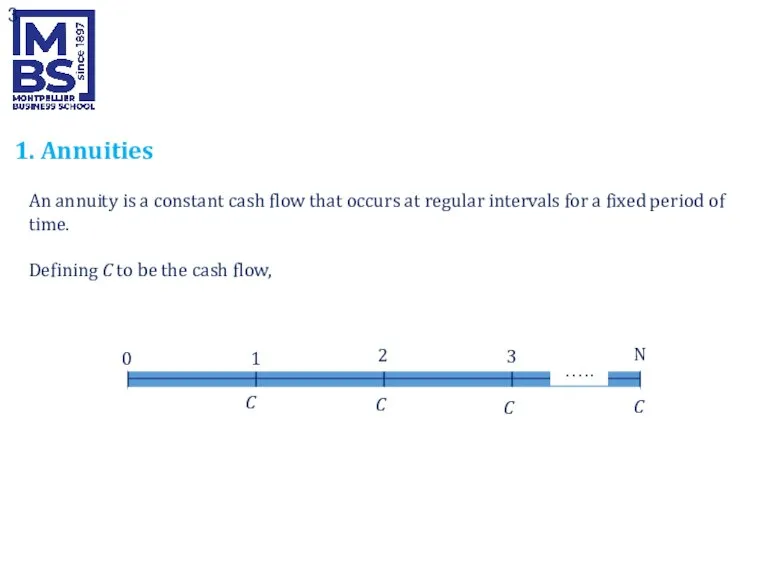
- 3. 1. Annuities An annuity is a constant cash flow that occurs at regular intervals for a
- 4. 1.1. Present Value of an Annuity The present value of an annuity can be calculated by
- 5. Exercise 1 What is the present value of an annuity of $1,000 for the next five
- 6. When the present value is known and the annuity is to be estimated, then: 1.2. Annuity,
- 7. 1. The future value of an end-of-the-period annuity can also be calculated as follows: 1.3. Future
- 8. Exercise 2 What is the future value of $1,000 each year for the next five years,
- 9. If we know the future value and we are looking for the annuity: 1.4. Annuity, given
- 10. Exercise 3: Saving for College Tuition 1. Assume that you want to send your newborn child
- 11. Solution for Exercise 3: Saving for College Tuition a. Expected tuition cost/year 18 years from now
- 12. Exercise 4: How much is an MBA worth? Assume that you were earning $40,000/year before entering
- 13. Solution for Exercise 4: How much is an MBA worth? 1. The MBA program is over
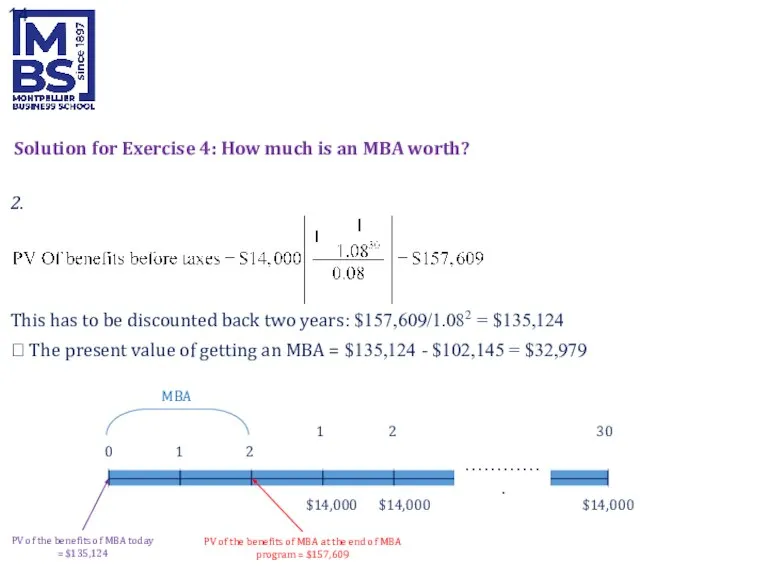
- 14. Solution for Exercise 4: How much is an MBA worth? 2. This has to be discounted
- 15. Exercise 5: Valuing a Straight Bond 1. You are trying to value a straight bond with
- 16. Solution for Exercise 5: Valuing a Straight Bond 1. You are trying to value a straight
- 17. 1. You are trying to value a straight bond with a fifteen year maturity, a 10.75%
- 18. 1. You are trying to value a straight bond with a fifteen year maturity, a 10.75%
- 19. A growing annuity is a cash flow growing at a constant rate for a specified period
- 20. The present value of a growing annuity can be estimated in all cases, but one -
- 21. Exercise 6: The Value of a Gold Mine Consider the example of a gold mine, where
- 22. A perpetuity is a constant cash flow at regular intervals forever. 2. Perpetuities …………………………… 0 2
- 23. Exercise 7: Valuing a Console Bond A console bond is a bond that has no maturity
- 24. A growing perpetuity is a cash flow that is expected to grow at a constant rate
- 26. Скачать презентацию





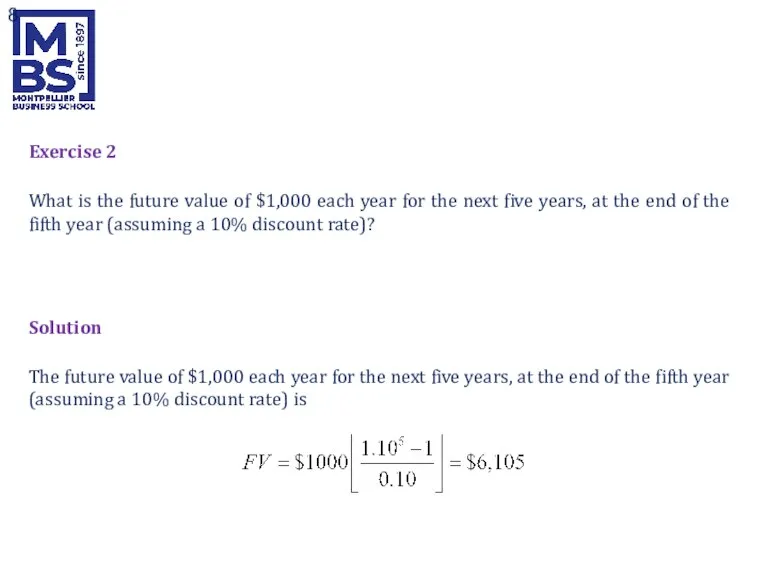















 Научно-исследовательская работа «Влияние наращивания на структуру и здоровье ногтей»
Научно-исследовательская работа «Влияние наращивания на структуру и здоровье ногтей»  Цифровые носители информации
Цифровые носители информации Остаться в живых
Остаться в живых Презентация на тему горы Южной Сибири
Презентация на тему горы Южной Сибири 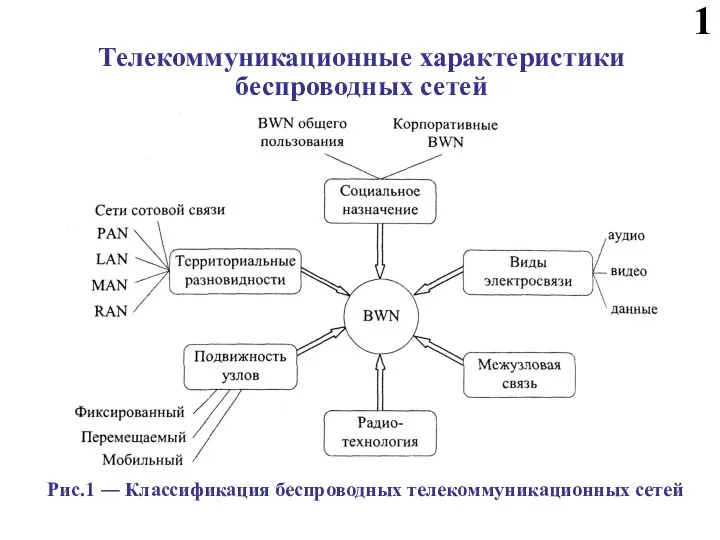 Идеология управления сетью в UMTS. Телекоммуникационные характеристики беспроводных сетей (часть 1)
Идеология управления сетью в UMTS. Телекоммуникационные характеристики беспроводных сетей (часть 1) Быт Японии
Быт Японии Испанская барочная живопись
Испанская барочная живопись Этот удивительный мир
Этот удивительный мир Презентация на тему Князья Киевской Руси
Презентация на тему Князья Киевской Руси  Православный храм
Православный храм Утилизация попутного нефтяного газа при освоении месторождений ООО «Нарьянмарнефтегаз». Проблемы и пути их решения.
Утилизация попутного нефтяного газа при освоении месторождений ООО «Нарьянмарнефтегаз». Проблемы и пути их решения. Презентация на тему Механизм разработки и установления вывозных таможенных пошлин
Презентация на тему Механизм разработки и установления вывозных таможенных пошлин  Региональная академия делового образования
Региональная академия делового образования Развлекательная программа на январь в рамках города Воронежа
Развлекательная программа на январь в рамках города Воронежа НИИ Спецвузавтоматика (Минобрнауки России)
НИИ Спецвузавтоматика (Минобрнауки России) Познай свой характер
Познай свой характер Гончарный промысел
Гончарный промысел «Дети и война»
«Дети и война» Презентация на тему Объект и диагностический инструментарий мониторинга результативности освоения детьми ООП дошкольного образ
Презентация на тему Объект и диагностический инструментарий мониторинга результативности освоения детьми ООП дошкольного образ МОУ Рождественская ООШ Карасукского района НСО Баязитов Алексей Андреевич Преподавание математики в классе с различным уровнем п
МОУ Рождественская ООШ Карасукского района НСО Баязитов Алексей Андреевич Преподавание математики в классе с различным уровнем п Басня
Басня Извлеченные уроки
Извлеченные уроки Советск – экологическая бомба? Насколько безопасно жить в городе Советске?
Советск – экологическая бомба? Насколько безопасно жить в городе Советске? Фалес
Фалес Презентация на тему Разнообразие и распространение организмов на Земле
Презентация на тему Разнообразие и распространение организмов на Земле Презентация на тему Н и НН в страдательных причастиях прошедшего времени
Презентация на тему Н и НН в страдательных причастиях прошедшего времени Метод круговой тренировки для повышения функциональных способностей боксеров
Метод круговой тренировки для повышения функциональных способностей боксеров Государственная (итоговая) аттестация выпускников 9 классов по алгебре и русскому языку в новой форме.
Государственная (итоговая) аттестация выпускников 9 классов по алгебре и русскому языку в новой форме.