Шар и сфера

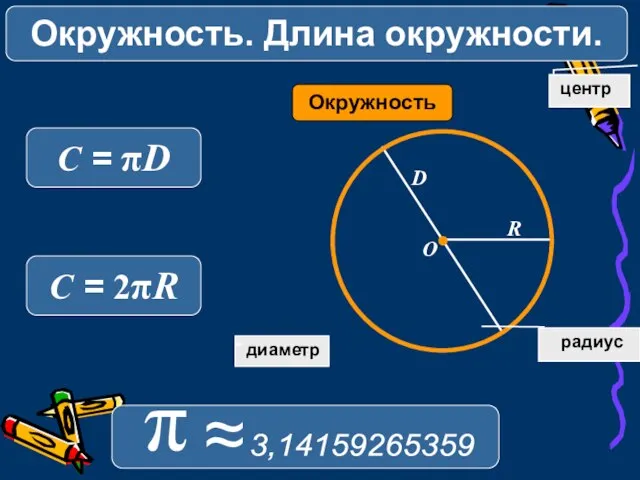
диаметр
Окружность
Колесо
центр
R
D
O
радиус
3,14159265359
π
≈
Окружность. Длина окружности.
C = πD
C = 2πR

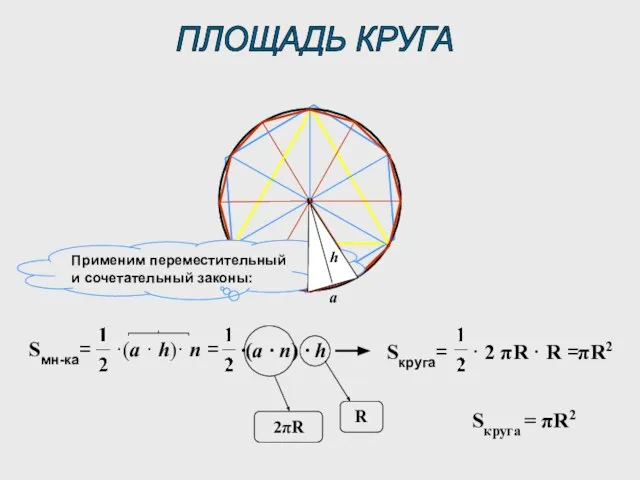
ПЛОЩАДЬ КРУГА
·(a · n) · h
πR2
Sкруга = πR2

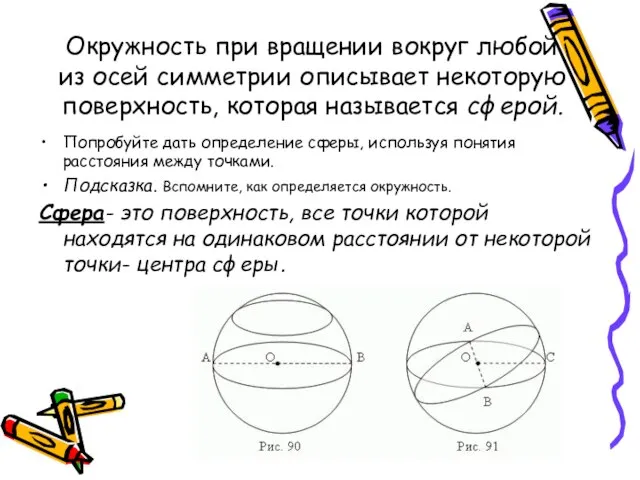
Окружность при вращении вокруг любой из осей симметрии описывает некоторую поверхность, которая называется сферой.
Попробуйте дать определение сферы, используя понятия расстояния между точками.
Подсказка. Вспомните, как определяется окружность.
Сфера- это поверхность, все точки которой находятся на одинаковом расстоянии от некоторой точки- центра сферы.

По аналогии с окружностью объясните, что такое: а)радиус; б)хорда; в)диаметр сферы.
Как окружность связана с кругом, так и сфера связана с шаром;
Шар-это часть пространства, ограниченная сферой.
У сферы и шара есть две главные формулы - формулы площади сферы и объема шара:
площадь сферы Sсферы=4πR2;
объем шара Vшара =4/3πR3.
С выводом этих формул вы познакомитесь только в старших классах, однако это не должно мешать вам использовать их уже сейчас.

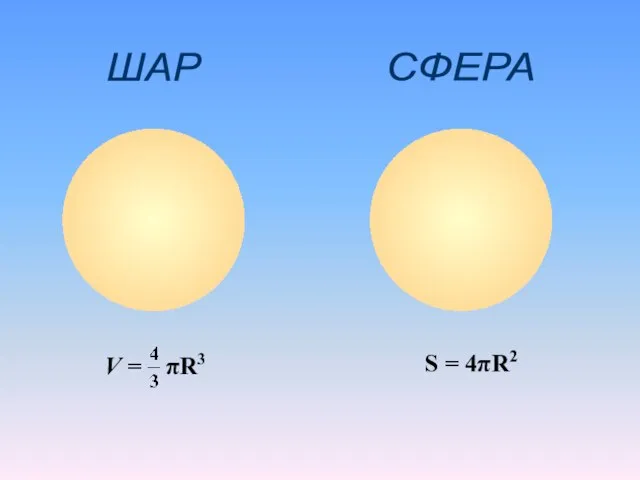
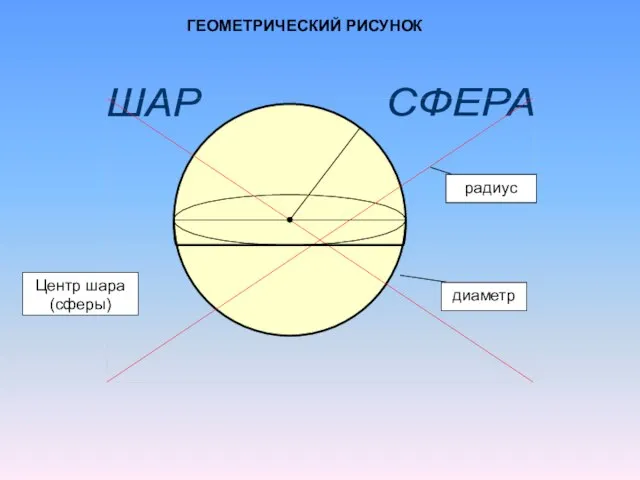
ШАР
СФЕРА
S = 4πR2

ШАР
СФЕРА
диаметр
радиус
Центр шара (сферы)
ГЕОМЕТРИЧЕСКИЙ РИСУНОК

Вычислительный центр.
Ребята, вы все сейчас становитесь членами вычислительного центра.
От вас требуется
внимательность,
сосредоточенность,
активность, точность.

Задача 1.
Найдите площадь поверхности шара радиусом 3м.
Какой объем имеет такой шар?

Задача 2.
Найдите радиус земного шара и площадь поверхности Земли.
(Радиус найдите с точностью до 100 км.)

Задача 3.
На рынке был куплен арбуз массой:
1)10 кг; б)16 кг.
Какие примерно у него радиус и площадь поверхности?
(Арбуз на 99% состоит из воды, 1 дм3 который имеет массу 1 кг)
Комментарий. Арбуз практически полностью состоит из воды, поэтому можно считать, что его масса 10 кг и, следовательно, объем 10 дм3.
Будем искать радиус шара объемом 10 дм3 :
10=4/3πR3≈4/3*3,14*R3 ≈4R3.
Найдем R из уравнения 10=4R3;
R3=2,5.
Подберем значение R с точностью до 1см.

Из таблицы видно, что радиус арбуза больше 13см, но меньше 14см. За приближенное значение радиуса можно взять любое из этих чисел, например 13.
По формуле площади сферы найдем
S=4π∙132≈4∙3,14∙169 ≈2100(см2).
Ответ: радиус арбуза 13 см,
площадь его поверхности 2100 см2.
Постарайтесь вспомнить эту задачу в конце летних каникул, когда встретитесь с арбузами ☺