Симметрия вокруг нас

«Я люблю математику не только потому, что она находит применение в технике, но и потому, что она красива»
(Р. Петер)

Цели
Рассмотреть различные виды симметрии.
Определить наиболее распространенные виды симметрии в окружающем нас мире.

Красота и разнообразие реальных объектов непосредственно связаны
с такими их свойствами, как симметричность, то есть
правильность, упорядоченность, повторяемость, гармония,
и, наоборот, асимметричность – неправильность,
нарушение порядка.

В поэзии и музыке, в живописи и архитектуре, в живой и неживой
природе существуют четкие закономерности, которые удивительным образом связаны
между собой. Для описания этих закономерностей в геометрии
рассматриваются несколько видов симметрии.

Осевая симметрия
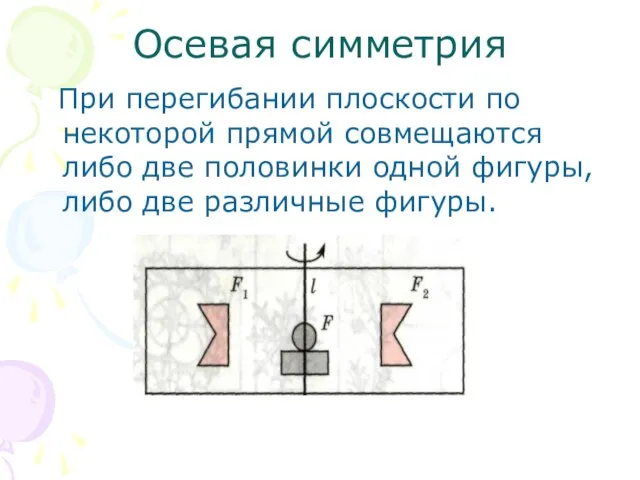
При перегибании плоскости по некоторой прямой совмещаются либо две половинки одной фигуры, либо две различные фигуры.

Поворотная симметрия
Наложим на лист бумаги с фигурой кальку и обведем фигуру.
Затем закрепим кальку в точке О и повернем ее на некоторый
угол. В результате фигура F1 переходит в фигуру F2.

Центральная симметрия
Центральная симметрия – поворот на 180. Центр поворота
Называется центром симметрии, а сами фигуры –
центрально-симметричными. При центральной симметрии
фигура может переходить сама в себя.

Параллельный перенос
Кальку с фигурой F просто сдвинем на расстояние d вдоль некоторой прямой.

Симметрия в природе
Симметрия форм, окраски цветов,
насекомых и животных
придает им красоту.