Simple Regression model

This is an example plot of linear function:
The nature of the relationship between variables can take many forms, ranging from simple mathematical functions to extremely complicated ones. The simplest relationship consists of a straight-line or linear relationship (linear function).

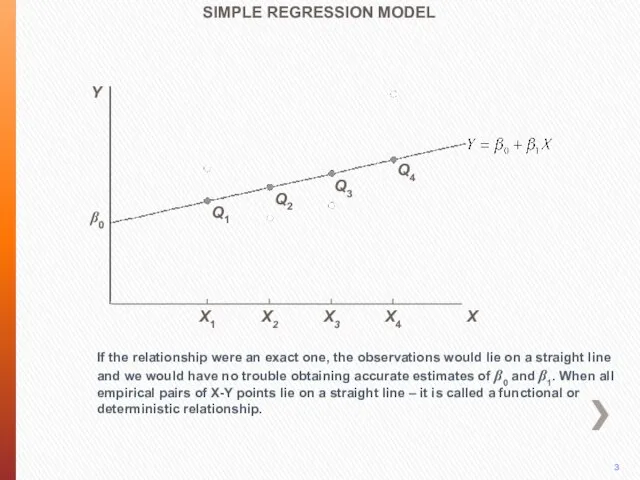
1
Y
SIMPLE REGRESSION MODEL
Suppose that a variable Y is a linear function of another variable X, with unknown parameters β0 and β1 that we wish to estimate.
β0
Suppose that we have a sample of 4 observations with X values as shown.

If the relationship were an exact one, the observations would lie on a straight line and we would have no trouble obtaining accurate estimates of β0 and β1. When all empirical pairs of X-Y points lie on a straight line – it is called a functional or deterministic relationship.
Q1
Q2
Q3
Q4
SIMPLE REGRESSION MODEL
3
β0
Y

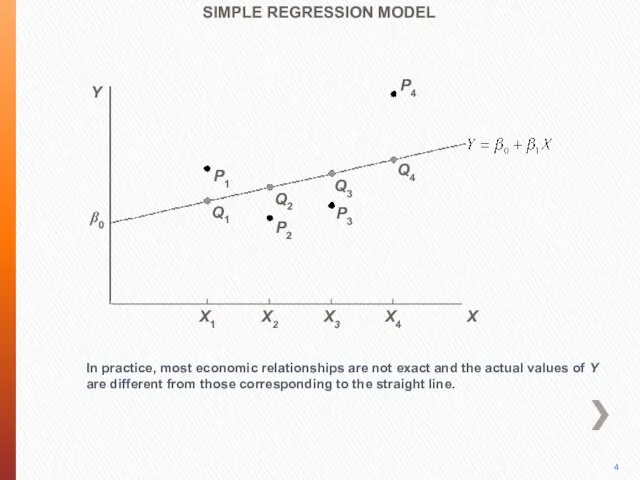
P4
In practice, most economic relationships are not exact and the actual values of Y are different from those corresponding to the straight line.
P3
P2
P1
Q1
Q2
Q3
Q4
SIMPLE REGRESSION MODEL
4
β0
Y

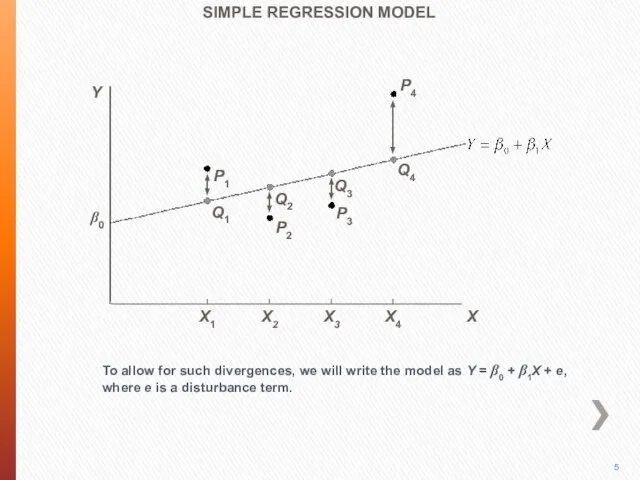
P4
To allow for such divergences, we will write the model as Y = β0 + β1X + e, where e is a disturbance term.
P3
P2
P1
Q1
Q2
Q3
Q4
SIMPLE REGRESSION MODEL
5
β0
Y

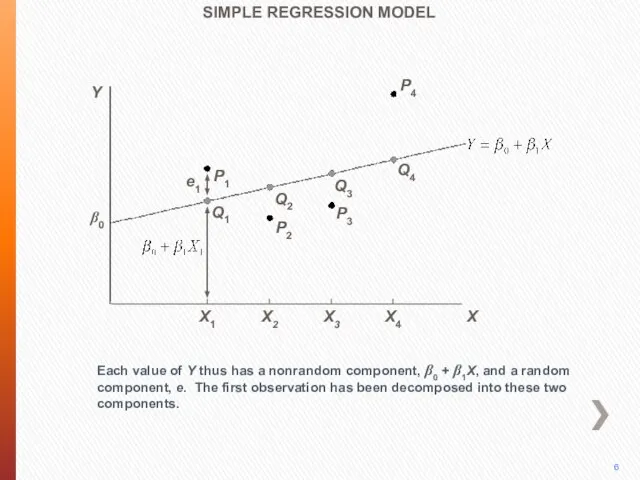
P4
Each value of Y thus has a nonrandom component, β0 + β1X, and a random component, e. The first observation has been decomposed into these two components.
P3
P2
P1
Q1
Q2
Q3
Q4
e1
SIMPLE REGRESSION MODEL
6
β0
Y

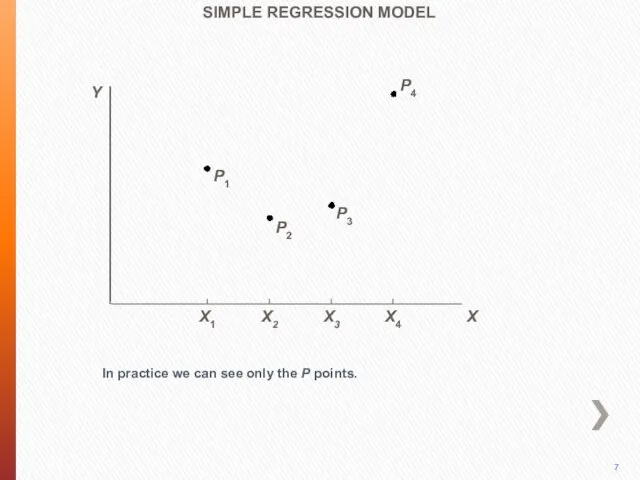
P4
In practice we can see only the P points.
P3
P2
P1
SIMPLE REGRESSION MODEL
7
Y

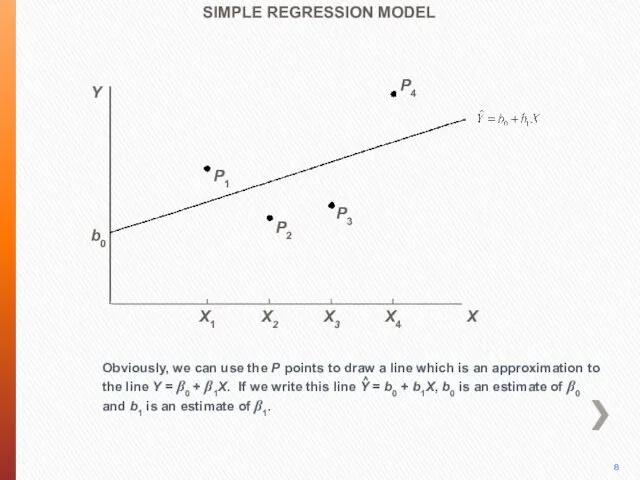
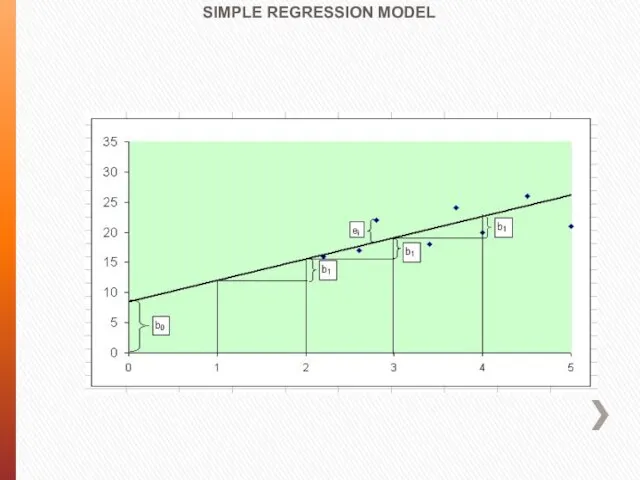
P4
Obviously, we can use the P points to draw a line which is an approximation to the line Y = β0 + β1X. If we write this line Y = b0 + b1X, b0 is an estimate of β0 and b1 is an estimate of β1.
P3
P2
P1
^
SIMPLE REGRESSION MODEL
8
b0
Y

However, we have obtained data from only a random sample of the population. For a sample, b0 and b1 can be used as estimates (estimators) of the respective population parameters β0 and β1
The intercept b0 and the slope b1 are the coefficients of the regression line. The slope b1 is the change in Y (increase, if >0, and decrease, if <0) associated with a unit change in X. The intercept is the value of Y when X=0; it’s the point at which the population regression line intersects the Y axis. In some cases the intercept has no real-world meaning (for example when X is the class size, Y is the test score – the intercept is the predicted value of test scores when there are no students in the class!).
Random error contains all the other factors besides X that determine the value of the dependent variable Y, for a specific observation.
SIMPLE REGRESSION MODEL

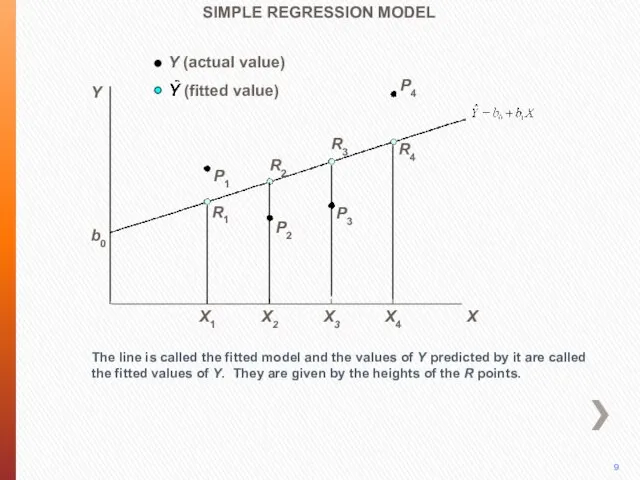
P4
The line is called the fitted model and the values of Y predicted by it are called the fitted values of Y. They are given by the heights of the R points.
P3
P2
P1
R1
R2
R3
R4
SIMPLE REGRESSION MODEL
9
b0
(fitted value)
Y (actual value)
Y

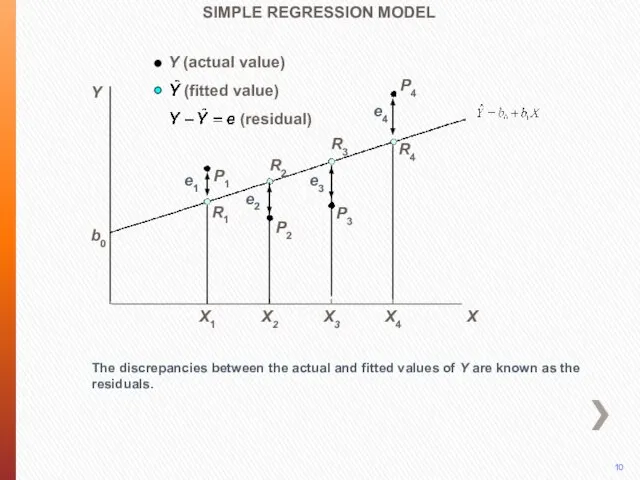
P4
The discrepancies between the actual and fitted values of Y are known as the residuals.
P3
P2
P1
R1
R2
R3
R4
(residual)
e1
e2
e3
e4
SIMPLE REGRESSION MODEL
10
b0
(fitted value)
Y (actual value)
Y

SIMPLE REGRESSION MODEL
Least squares criterion:
Minimize SSE (residual sum of squares), where
To begin with, we will draw the fitted line so as to minimize the sum of the squares of the residuals, SSE. This is described as the least squares criterion.
19

SIMPLE REGRESSION MODEL
Why the squares of the residuals? Why not just minimize the sum of the residuals?
Least squares criterion:
Why not minimize
20
Minimize SSE (residual sum of squares), where

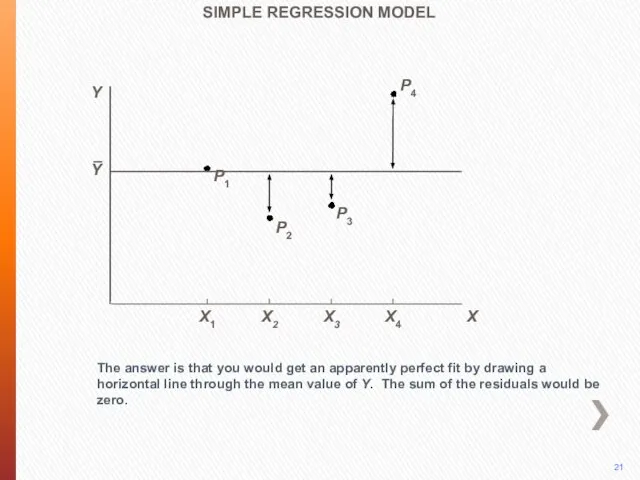
P4
The answer is that you would get an apparently perfect fit by drawing a horizontal line through the mean value of Y. The sum of the residuals would be zero.
P3
P2
P1
SIMPLE REGRESSION MODEL
21
Y

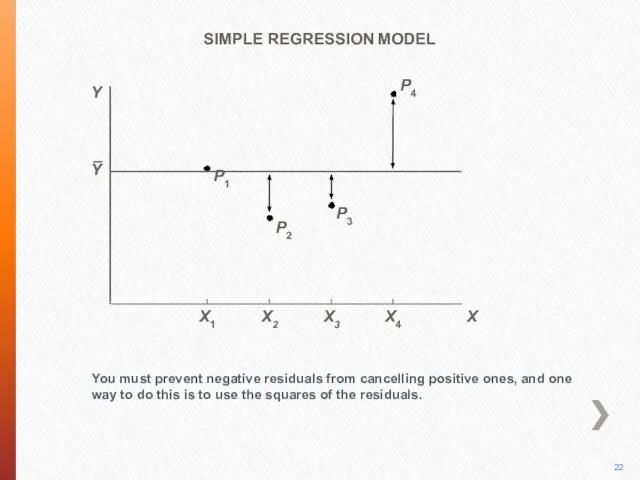
P4
You must prevent negative residuals from cancelling positive ones, and one way to do this is to use the squares of the residuals.
P3
P2
P1
SIMPLE REGRESSION MODEL
22
Y

SIMPLE REGRESSION MODEL
Since we are minimizing
which has two unknowns, b0 and b1. A mathematical technique which determines the values of b0 and b1 that best fit the observed data is known as the Ordinary Least Squares method (OLS).
Ordinary Least Squares is a procedure that selects the best fit line given a set of data points, by minimizing the sum of the squared deviations of the points from a line. That is, if is the equation of the best line to fit through the data then in order to get this best line, using the least squares criteria, for each value data point (xi,yi) if where , then ei is the amount of deviation of the data point from the line. The least squares criteria minimizes, finds the slope b1 and the y-intercept b0 from the data, that minimizes the sum of the square deviations, .

SIMPLE REGRESSION MODEL
For the mathematically curious , I provide a condensed derivation of the coefficients.
To minimize determine the
partial derivatives with respect to b0 and with respect to b1. These are:
Setting and solving for b0 and b1 results in equations given below.

Since there are two equations with two unknown, we can solve these equations simultaneously for b0 and b1 as follows:
ONLY FOR REGRESSION MODELS WITH ONE INDEPENDENT VARIABLE!
We also note that the regression line always goes through the mean ( ).
SIMPLE REGRESSION MODEL

SIMPLE REGRESSION MODEL
In matrix notation OLS may be written as:
Y = Xb + e
The normal equations in matrix form are now
XT Y = XTXb
And when we solve it for b we get:
b = (XTX)-1XTY
where Y is a column vector of the Y values and X is a matrix containing a column of ones (to pick up the intercept) followed by a column of the X variable containing the observations on it and b is a vector containing the estimators of regression parameters.

SIMPLE REGRESSION MODEL
We can state as follows:
How to inverse XTX?
1. matrix determinant
2. minor matrix
3. cofactor matrix
4. inverse matrix

SIMPLE REGRESSION MODEL
EXAMPLE
In this problem we were looking at the way home size is effected by the family income. We will use this model to try to predict the value of the dependent variable based on the independent variable. Also, the slope will help us to understand how the Y variable changes for each unit change in the X variable.
Assume a real-estate developer is interested in determining the relationship between family income (X, in thousand of dollars) of the local resident and the square footage of their homes (Y, in hundreds of square feet). A random sample of ten families is obtained with the following results:

SIMPLE REGRESSION MODEL

SIMPLE REGRESSION MODEL

SIMPLE REGRESSION MODEL

Let’s try another example:
X – commercial time (minutes) Y – sales ($ hundred thousand)

REGRESSION MODEL WITH TWO EXPLANATORY VARIABLES

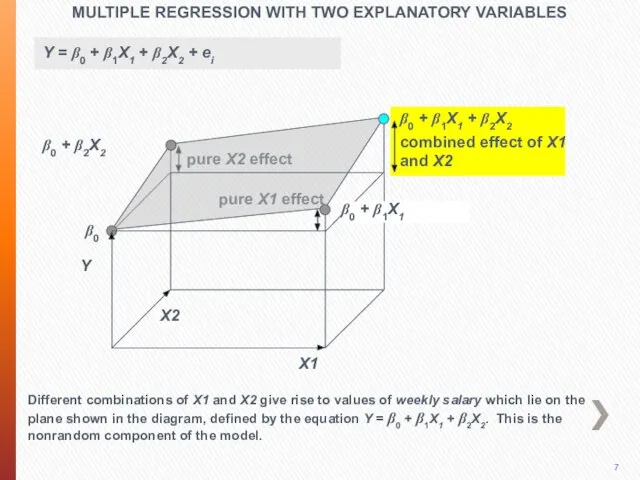
MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
Y
X2
X1
β0
1
This sequence provides a geometrical interpretation of a multiple regression model with two explanatory variables.
Y – weekly salary ($)
X1 – length of employment (in months)
X2 – age (in years)
Specifically, we will look at weekly salary function model where weekly salary, Y,
depend on length of employment X1, and age, X2.

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
Y
X2
X1
β0
3
The model has three dimensions, one each for Y, X1, and X2. The starting point for investigating the determination of Y is the intercept, β0.
Y – weekly salary ($)
X1 – length of employment (in months)
X2 – age (in years)

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
Y
X2
X1
β0
4
Literally the intercept gives weekly salary for those respondents who have no age (??)
and no length of employment (??). Hence a literal interpretation of β0 would be unwise.
Y – weekly salary ($)
X1 – length of employment (in months)
X2 – age (in years)

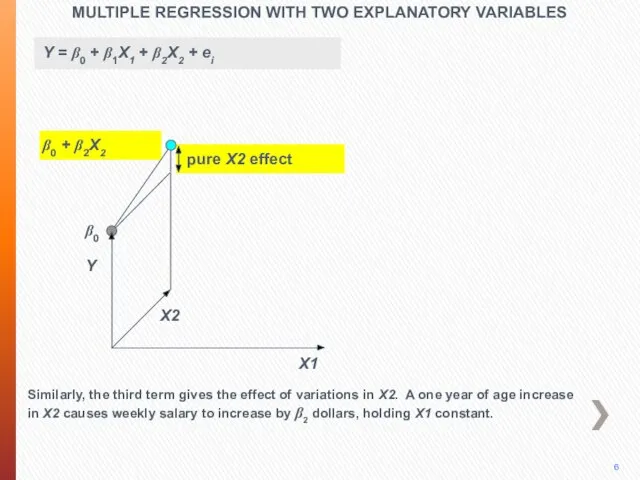
MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
5
Y
X2
The next term on the right side of the equation gives the effect of X1. A one month of employment increase in X1 causes weekly salary to increase by β1dollars, holding X2 constant.
X1
β0
pure X1 effect
β0 + β1X1
Y – weekly salary ($)
X1 – length of employment (in months)
X2 – age (in years)

pure X2 effect
MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
X1
β0
β0 + β2X2
Y
X2
6
Similarly, the third term gives the effect of variations in X2. A one year of age increase
in X2 causes weekly salary to increase by β2 dollars, holding X1 constant.

pure X2 effect
pure X1 effect
MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
X1
β0
β0 + β2X2
β0 + β1X1 + β2X2
Y
X2
β0 + β1X1
combined effect of X1 and X2
7
Different combinations of X1 and X2 give rise to values of weekly salary which lie on the plane shown in the diagram, defined by the equation Y = β0 + β1X1 + β2X2. This is the nonrandom component of the model.

pure X2 effect
pure X1 effect
MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
X1
β0
β0 + β2X2
β0 + β1X1 + β2X2
β0 + β1X1 + β2X2+ ei
Y
X2
combined effect of X1 and X2
e
8
The final element of the model is the error term, e. This causes the actual values of Y to deviate from the plane. In this observation, e happens to have a positive value.
β0 + β1X1

pure X2 effect
pure X1 effect
MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
X1
β0
β0+ β1X1+ β2X2
β0 + β1X1 + β2X2 + e
Y
X2
combined effect of X1 and X2
e
9
A sample consists of a number of observations generated in this way. Note that the interpretation of the model does not depend on whether X1 and X2 are correlated or not.
β0 + β1X1
β0 + β2X2

pure X2 effect
pure X1 effect
MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
10
X1
β0
β0 + β1X1+ β2X2
β0 + β1X1 + β2X2+ e
Y
X2
combined effect of X1 and X2
e
However we do assume that the effects of X1 and X2 on salary are additive.
The impact of a difference in X1 on salary is not affected by the value of X2, or vice versa.
β0 + β1X1
β0 + β2X2

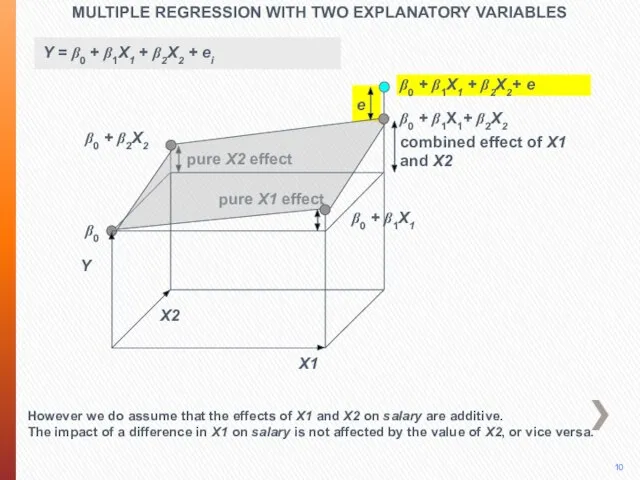
Slope coefficients are interpreted as partial slope/partial regression coefficients:
? b1 = average change in Y associated with a unit change in X1, with the other independent variables held constant (all else equal);
? b2 = average change in Y associated with a unit change in X2, with the other independent variables held constant (all else equal).
MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
The regression coefficients are derived using the same least squares principle used in simple regression analysis. The fitted value of Y in observation i depends on our choice of b0, b1, and b2.
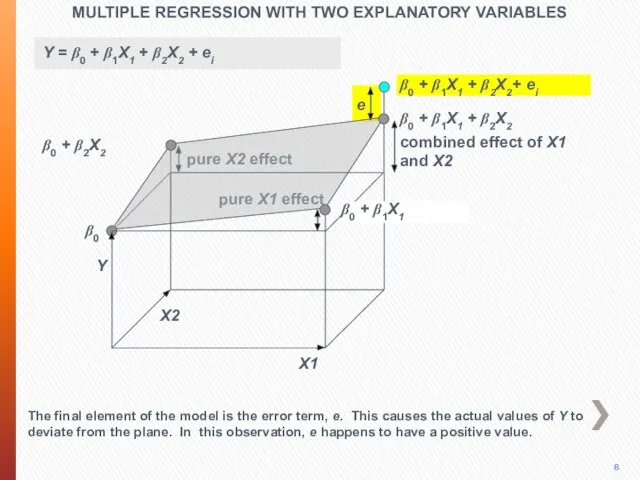
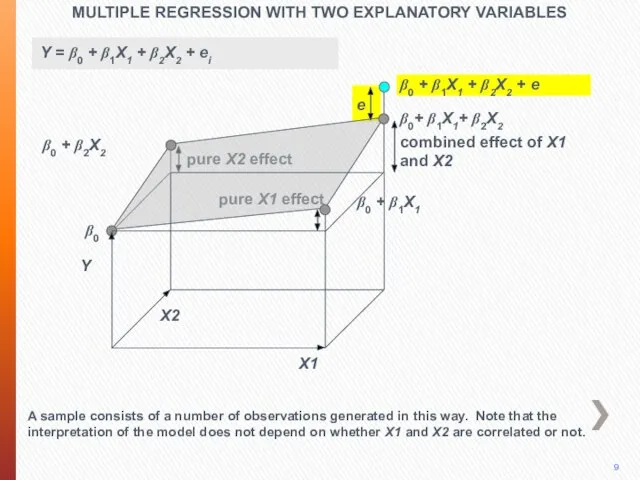
11

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
The residual ei in observation i is the difference between the actual and fitted values of Y.
12

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
We define SSE, the sum of the squares of the residuals, and choose b0, b1, and b2
so as to minimize it.
13

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
First we expand SSE as shown, and then we use the first order conditions for minimizing it.
14

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
We thus obtain three equations in three unknowns. Solving for b0, b1, and b2,
we obtain the expressions shown above.
15

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
The expression for b0 is a straightforward extension of the expression for it in simple regression analysis.
16

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
However, the expressions for the slope coefficients are considerably more complex than that for the slope coefficient in simple regression analysis.
17

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES
For the general case when there are many explanatory variables, ordinary algebra is inadequate. It is necessary to switch to matrix algebra.
18

In matrix notation OLS may be written as:
Y = Xb + e
The normal equations in matrix form are now
XT Y = XTXb
And when we solve it for b we get:
b = (XTX)-1XTY
where Y is a column vector of the Y values and X is a matrix containing a column of ones (to pick up the intercept) followed by a column of the X variables containing the observations on them and b is a vector containing the estimators of regression parameters.
MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES

MATRIX ALGEBRA: SUMMARY
A vector is a collection of n numbers or elements, collected either in a column (a column vector) or in a row (a row vector).
A matrix is a collection, or array, of numbers of elements in which the elements are laid out in columns and rows. The dimension of matrix is n x m where n is the number of rows and m is the number of columns.
Types of matrices
A matrix is said to be square if the number of rows equals the number of columns.
A square matrix is said to be symmetric if its (i, j) element equals its (j, i) element.
A diagonal matrix is a square matrix in which all the off-diagonal elements equal zero, that is, if the square matrix A is diagonal, then aij =0 for i≠j.
The transpose of a matrix switches the rows and the columns. That is, the transpose of a matrix turns the n x m matrix A into the m x n matrix denoted by AT, where the (i, j) element of A becomes the (j, i) element of AT; said differently, the transpose of a matrix A turns the rows of A into the columns of AT. The inverse of the matrix A is defined as the matrix for which A-1A=1. If in fact the inverse matrix A-1 exists, then A is said to be invertible or nonsingular.
Vector and matrix multiplication
The matrices A and B can be multiplied together if they are conformable, that is, if the number of columns of A equals the number of rows of B. In general, matrix multiplication does not commute, that is, in general AB≠ BA.

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES: EXAMPLE
Data for weekly salary based upon the length of employment and
age of employees of a large industrial corporation are shown in the table.
Calculate the OLS estimates for regression coefficients for the available sample. Comment on your results.

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES: EXAMPLE
Y-weekly salary ($) X1 –length of employment (months) X2-age (years)

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES: EXAMPLE

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES: EXAMPLE
Y-weekly salary ($) X1 –length of employment (months) X2-age (years)
Our regression equation with two predictors (X1, X2):

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES: EXAMPLE
These are our data points in 3dimensional space (graph drawn using Statistica 6.0)
X1
X1
Y
X2

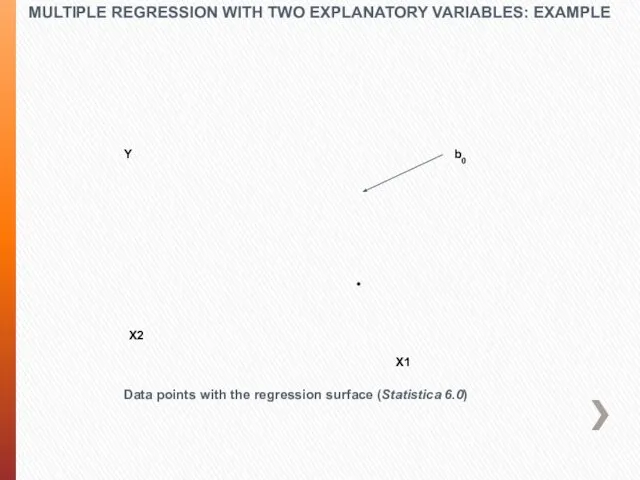
MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES: EXAMPLE
Data points with the regression surface (Statistica 6.0)
X1
X2
Y
b0

MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES: EXAMPLE
Data points with the regression surface (Statistica 6.0) after rotation.
Y
X1
X2

There are times when a variable of interest in a regression cannot possibly be considered quantitative. An example is the variable gender.
Although this variable may be considered important in predicting a quantitative dependent variable, it cannot be regarded as quantitative.
Dummy variables
in econometric models
The best course of action in such case is to take separate samples of males and females and conduct two separate regression analyses.
The results for the males can be compared with the results for the females to see if the same predictor variables and the same regression coefficients results.

If a large sample size is not possible, a dummy variable can be employed to introduce qualitative variable into the analysis.
A DUMMY VARIABLE
IN A REGRESSION ANALYSIS
IS A QUALITATIVE OR CATEGORICAL VARIABLE THAT IS USED AS A PREDICTOR VARIABLE.

For example, a male could be designated with the code 0 and the female could be coded as 1.
Each person sampled could then be measured as either a 0 or a 1 for the variable gender, and this variable, along with the quantitative variables for the persons, could be entered into a multiple regression program and analyzed.

Example 1
Returning to real-estate developer, we noticed that all the houses in the population were from three neighborhoods, A, B, and C.

Using these data, we can construct the necessary dummy variables and determine whether they contribute significantly to the prediction of home size (Y).
One way to code neighborhoods would be to define:

However, this type of coding has many problems. First, because 0 < 1< 2, the codes imply that neighborhood A is smaller then neighborhood B, which is smaller then neighborhood C. A better procedure is to use the necessary number of dummy variables to represent the neighborhood.

To represent the three neighborhoods, we use two dummy variables, by letting

What happened to neighborhood C? It is not necessary to develop a third dummy variable.
IT IS VERY IMPORTANT
THAT YOU NOT INCLUDE IT!!
If you attempted to use three such dummy variables in your model, you would receive a message in your computer output informing you that no solution exists for this model.

Why?
One predictor variable is a linear combination (including a constant term) of one or more other predictors, then mathematically no solution exists for the least squares coefficients. To arrive at a usable equation, any such predictor variable must not be included. We don’t lose any information – this excluded category is the reference system. The coefficients are the measure of the categories included in comparison to this one excluded.

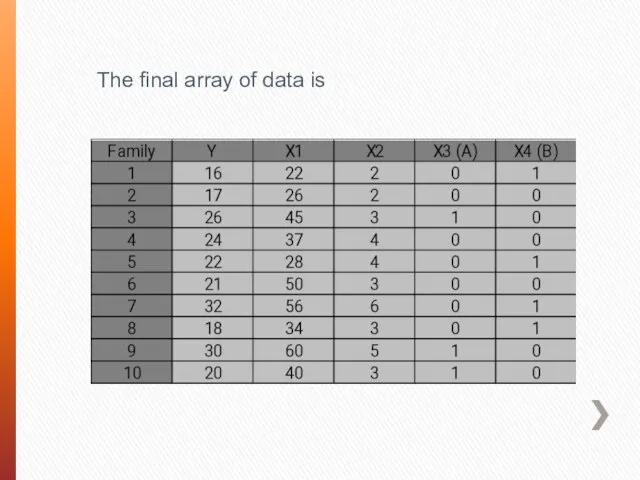
The final array of data is

· If family income increases 1000$ the average home size will increase about 0,082 hundred of square feet (holding family size constant)
· If family size increases 1 person the average home size will increase about 3,27 hundred of square feet (holding family income constant)

· The houses located in neighborhood A are 1,613 hundred of square feet bigger then houses from neighborhood C.
· The houses located in neighborhood B are 0,9 hundred of square feet smaller then houses from neighborhood C.

Example 2
Joanne Herr, an analyst for the Best Foods grocery chain, wanted to know whether three stores have the same average dollar amount per purchase or not. Stores can be thought of a single qualitative variable set at 3 levels – A, B, and C.

A model can be set up to predict the dollar amount per purchase:
where
Y^- expected dollar amount per purchase

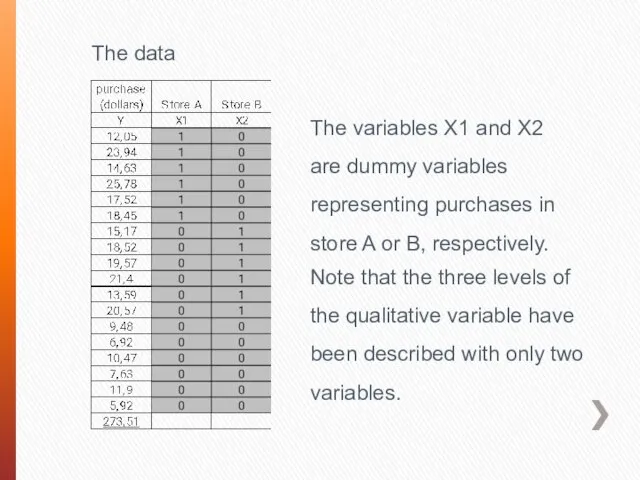
The data
The variables X1 and X2 are dummy variables representing purchases in store A or B, respectively.
Note that the three levels of the qualitative variable have been described with only two variables.

The regression equation

· the average dollar amount per purchase is for store A
is 10,01$ higher comparing with store C
· the average dollar amount per purchase is for store B
is 9,42$ higher comparing with store C
always compare to the excluded category!!