Содержание
- 2. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES Y X2 X1 β0 1 This sequence provides a geometrical
- 3. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES Y X2 X1 β0 3 The model has three dimensions,
- 4. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES Y X2 X1 β0 4 Literally the intercept gives weekly
- 5. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES 5 Y X2 The next term on the right side
- 6. pure X2 effect MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES X1 β0 β0 + β2X2 Y X2
- 7. pure X2 effect pure X1 effect MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES X1 β0 β0 +
- 8. pure X2 effect pure X1 effect MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES X1 β0 β0 +
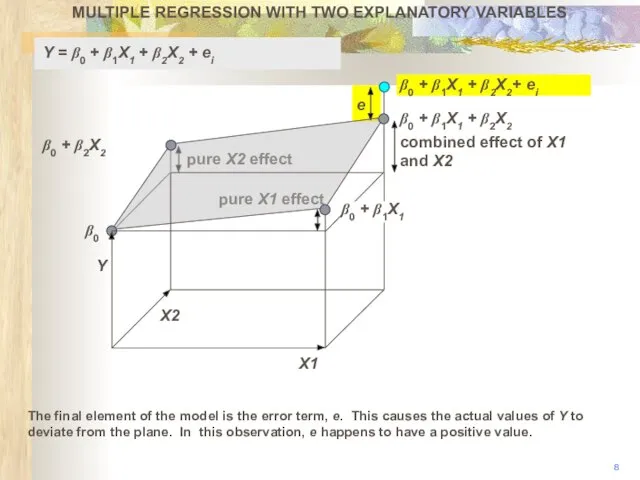
- 9. pure X2 effect pure X1 effect MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES X1 β0 β0+ β1X1+
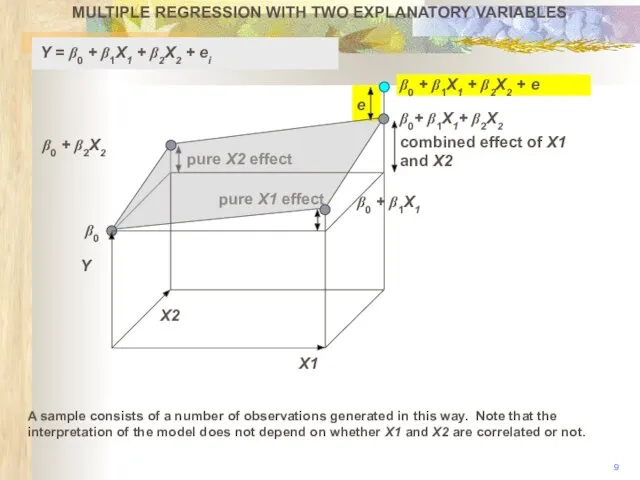
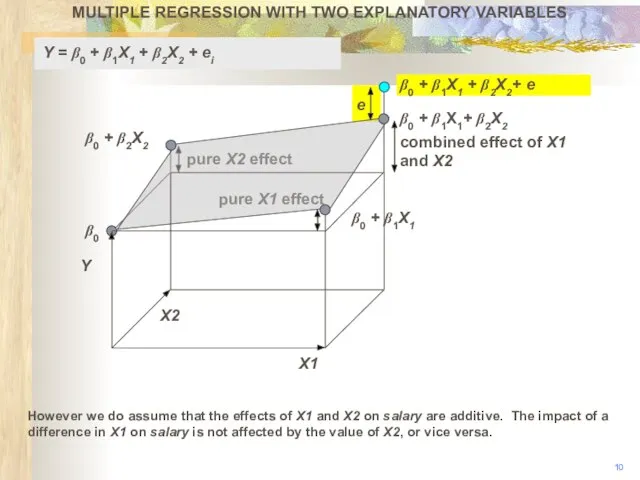
- 10. pure X2 effect pure X1 effect MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES 10 X1 β0 β0
- 11. Slope coefficients are interpreted as partial slope/partial regression coefficients: ? b1 = average change in Y
- 12. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES The regression coefficients are derived using the same least squares
- 13. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES The residual ei in observation i is the difference between
- 14. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES We define SSE, the sum of the squares of the
- 15. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES First we expand SSE as shown, and then we use
- 16. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES We thus obtain three equations in three unknowns. Solving for
- 17. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES The expression for b0 is a straightforward extension of the
- 18. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES However, the expressions for the slope coefficients are considerably more
- 19. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES For the general case when there are many explanatory variables,
- 20. In matrix notation OLS may be written as: Y = Xb + e The normal equations
- 21. MATRIX ALGEBRA: SUMMARY A vector is a collection of n numbers or elements, collected either in
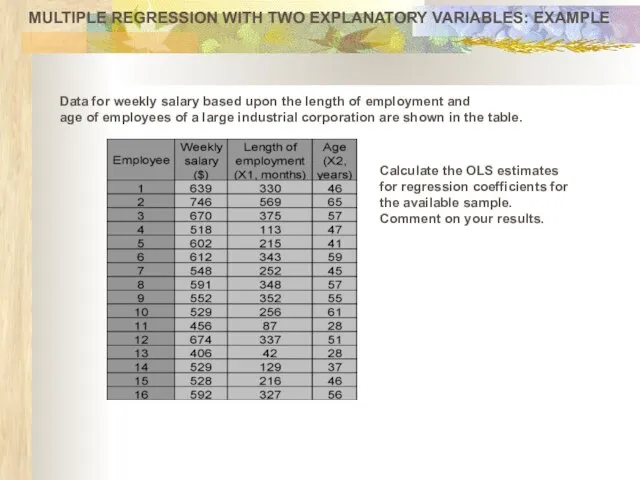
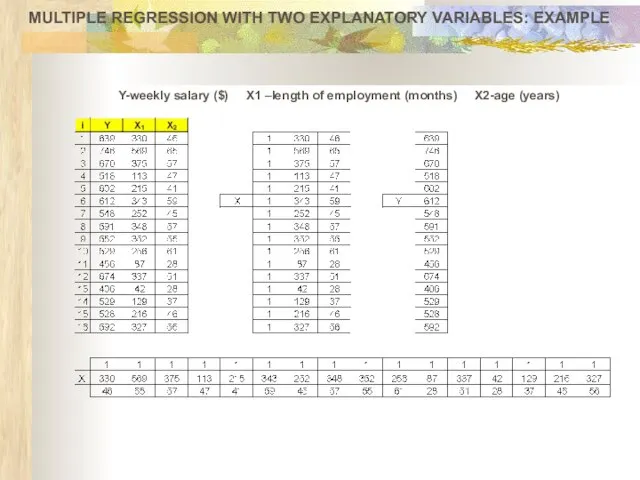
- 22. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES: EXAMPLE Data for weekly salary based upon the length of
- 23. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES: EXAMPLE Y-weekly salary ($) X1 –length of employment (months) X2-age
- 24. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES: EXAMPLE
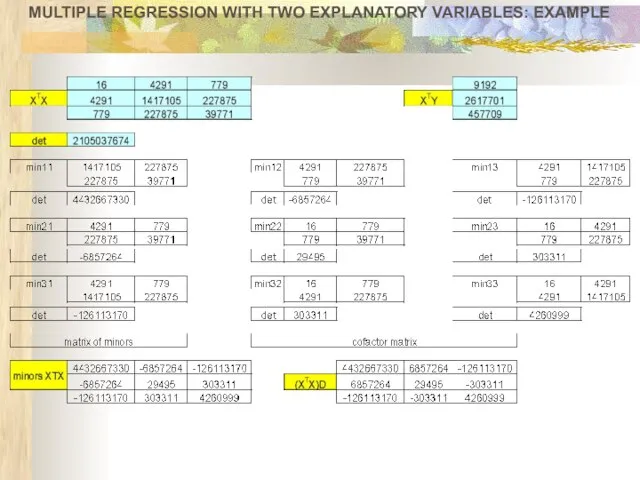
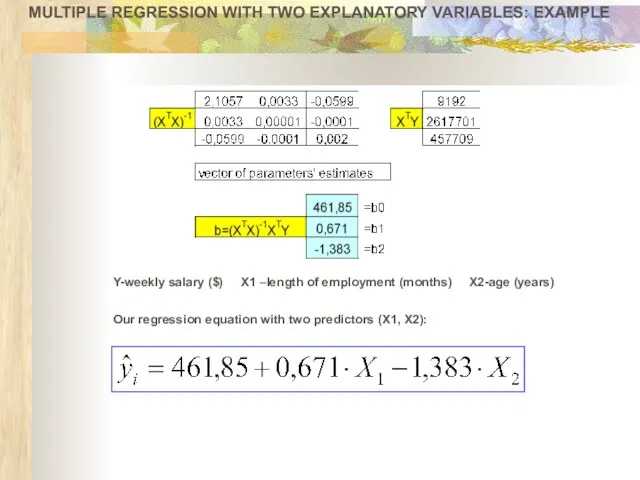
- 25. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES: EXAMPLE Y-weekly salary ($) X1 –length of employment (months) X2-age
- 26. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES: EXAMPLE These are our data points in 3dimensional space (graph
- 27. MULTIPLE REGRESSION WITH TWO EXPLANATORY VARIABLES: EXAMPLE Data points with the regression surface (Statistica 6.0) X1
- 29. Скачать презентацию



















 ВТОРОЙ ЗАКОН НЬЮТОНА
ВТОРОЙ ЗАКОН НЬЮТОНА Ансамбль народного танца Алан
Ансамбль народного танца Алан Влияние основных факторов на динамику индекса (S&P)
Влияние основных факторов на динамику индекса (S&P) Географические координаты на карте России
Географические координаты на карте России Развитие рынка акций эмитента: Индексы РТС и Срочный рынок РТС
Развитие рынка акций эмитента: Индексы РТС и Срочный рынок РТС Полякова Лариса Александровна. Техника Правополушарное рисование на тему: Море
Полякова Лариса Александровна. Техника Правополушарное рисование на тему: Море Разделительный мягкий знак
Разделительный мягкий знак ИЗУЧИТЕ ЭТО ИЗНУТРИ: социальные сети, блогосфера и User-Created Content. Как подружиться с новой средой
ИЗУЧИТЕ ЭТО ИЗНУТРИ: социальные сети, блогосфера и User-Created Content. Как подружиться с новой средой Гематогенный остеомиелит
Гематогенный остеомиелит  Плод. Разнообразие и значение плодов
Плод. Разнообразие и значение плодов жизнь и творчество Василия макаровича Шукшина
жизнь и творчество Василия макаровича Шукшина Роль детско-родительских отношении в формировании психосоматической болезни.
Роль детско-родительских отношении в формировании психосоматической болезни. Устный опрос по теме «Логарифм»
Устный опрос по теме «Логарифм» Презентация на тему Коррекционная группа
Презентация на тему Коррекционная группа Система оплаты труда сотрудников самовывозов и пунктов выдачи заказов интернет магазина Wildberries
Система оплаты труда сотрудников самовывозов и пунктов выдачи заказов интернет магазина Wildberries Презентация на тему Сущность функционального подхода к управлению таможенными органами
Презентация на тему Сущность функционального подхода к управлению таможенными органами  Мочевыделительная система
Мочевыделительная система Мечтай правильно или как прожить жизнь своей мечты
Мечтай правильно или как прожить жизнь своей мечты SO, TOO, ALSO NEITHER , EITHER
SO, TOO, ALSO NEITHER , EITHER  Трудные случаи таблицы умножения и деления
Трудные случаи таблицы умножения и деления Спецрисунок и художественная графика. Рисунок фигуры в положение контрапост, в одежде. Черно-белая и цветная графика фигуры
Спецрисунок и художественная графика. Рисунок фигуры в положение контрапост, в одежде. Черно-белая и цветная графика фигуры Социально-экономическое развитие Северо-Кавказского федерального округа в I полугодии 2011 года
Социально-экономическое развитие Северо-Кавказского федерального округа в I полугодии 2011 года Экскурсия по городу. Промышленный туризм для младших школьников
Экскурсия по городу. Промышленный туризм для младших школьников Памятники Москвы
Памятники Москвы Участие родителей в коррекционно-воспитательной работе по преодолению речевых нарушений у детей дошкольного возраста
Участие родителей в коррекционно-воспитательной работе по преодолению речевых нарушений у детей дошкольного возраста Ты и твое здоровье
Ты и твое здоровье Николай Хмеленок. Тренажёры по английскому языку. Расположите по порядку. Признаки
Николай Хмеленок. Тренажёры по английскому языку. Расположите по порядку. Признаки Конституция Российской Федерации
Конституция Российской Федерации