Содержание
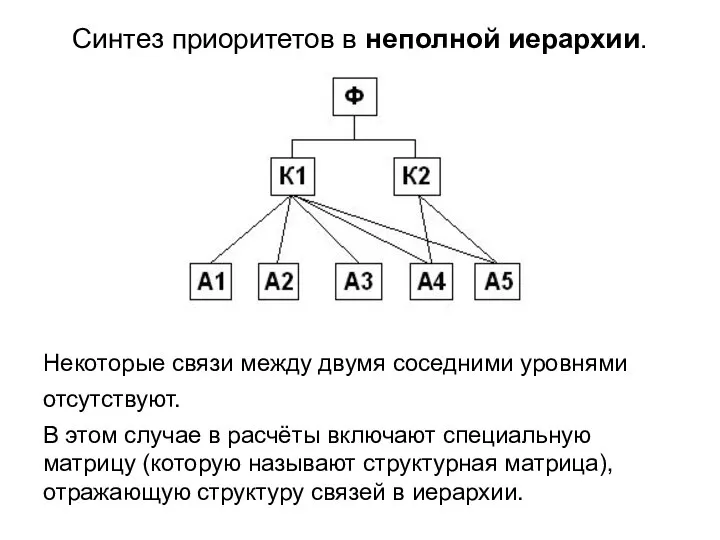
- 2. Синтез приоритетов в неполной иерархии. Некоторые связи между двумя соседними уровнями отсутствуют. В этом случае в
- 3. Структурная матрица. К1 К2 … Кn L= Где Ri - число элементов-потомков элемента Ki, N- число
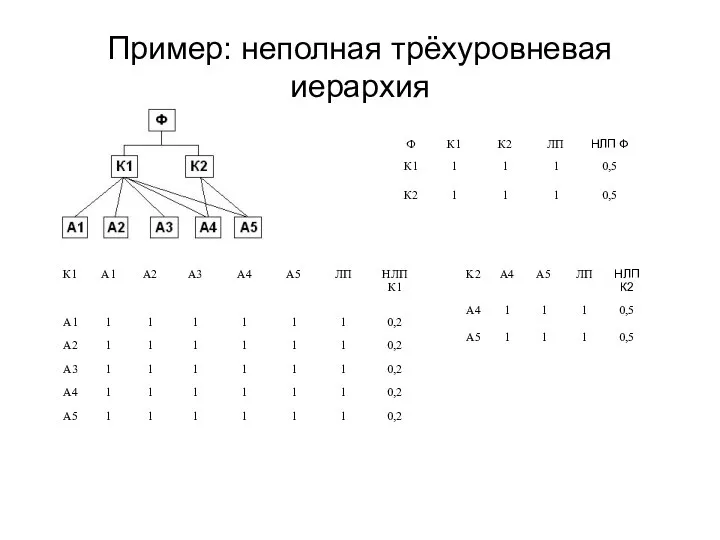
- 4. Пример: неполная трёхуровневая иерархия
- 5. Строим вспомогательные матрицы А= L=
- 6. Синтез приоритетов
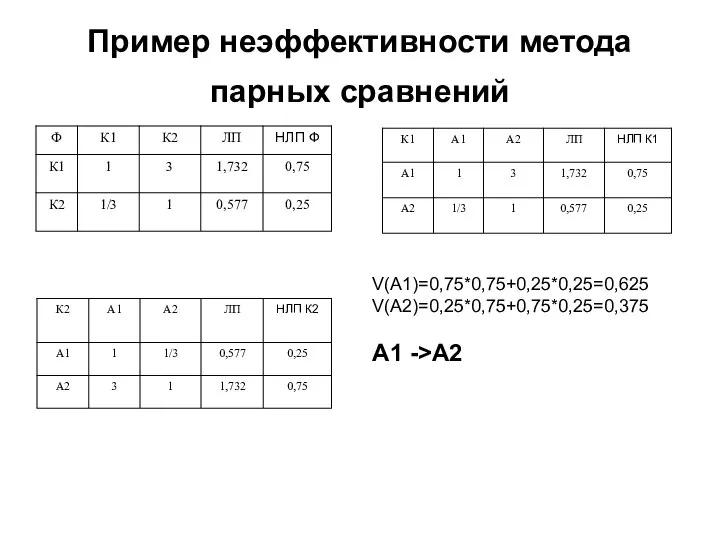
- 7. Пример неэффективности метода парных сравнений V(A1)=0,75*0,75+0,25*0,25=0,625 V(A2)=0,25*0,75+0,75*0,25=0,375 A1 ->A2
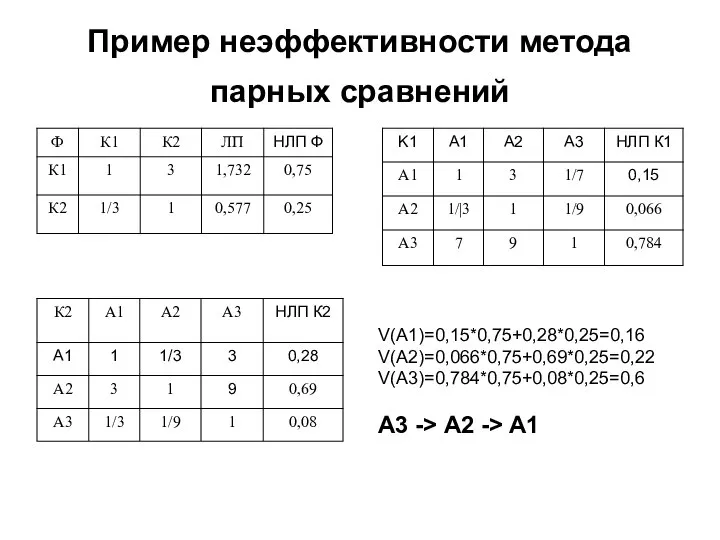
- 8. Пример неэффективности метода парных сравнений V(A1)=0,15*0,75+0,28*0,25=0,16 V(A2)=0,066*0,75+0,69*0,25=0,22 V(A3)=0,784*0,75+0,08*0,25=0,6 А3 -> A2 -> A1
- 9. метод сравнения элементов относительно стандарта Метод попарных сравнений может быть неудобен в некоторых случаях: Когда альтернативы
- 10. метод сравнения элементов относительно стандарта Стандарт устанавливает уровень качества объекта относительно критерия качества. Например, критерий «ликвидность»
- 11. метод сравнения элементов относительно стандарта Стандарты стараются делать не абстрактными, а отождествлять их с некоторыми реальными
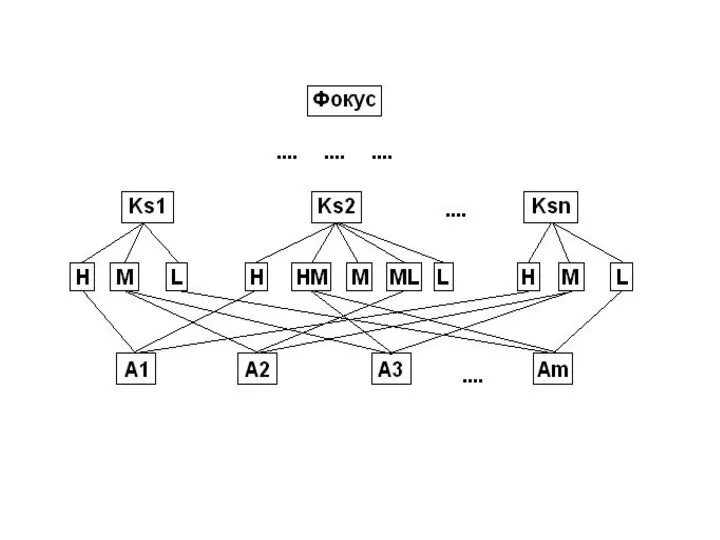
- 12. метод сравнения элементов относительно стандарта Стандарты помещают в иерархию, вводя для них дополнительный уровень — между
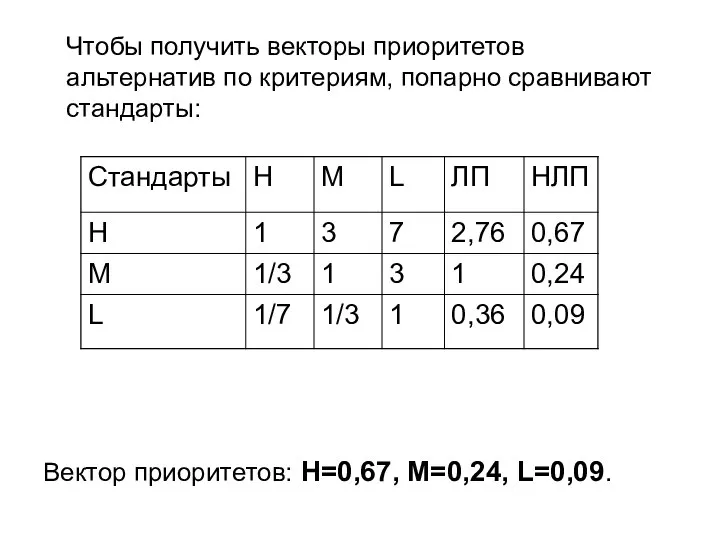
- 14. Чтобы получить векторы приоритетов альтернатив по критериям, попарно сравнивают стандарты: Вектор приоритетов: H=0,67, M=0,24, L=0,09.
- 15. метод сравнения элементов относительно стандарта Далее составляют вектор приоритетов для альтернатив по данному критерию. Числовые значения
- 16. метод сравнения элементов относительно стандарта Дальнейшие расчеты по алгоритму МАИ: после того, как получили векторы локальных
- 17. метод сравнения элементов относительно стандарта A = - численное значение стандартов, соответствующее альтернативе Ai по данному
- 18. Для получения нормированных приоритетов: , где [S] =
- 19. Сравнение объектов методом копирования Разделим альтернативы на два множества: А={А1, А2, …, Аn} В={В1, В2, …,
- 20. Пример: Пусть для анализа поступают две новые альтернативы, свойства которых по данному критерию полностью идентичны свойствам
- 21. Оценка согласованности иерархии Шаг 1. Подсчет максимального собственного числа матрицы парных сравнений: где - нормированный вектор
- 22. Шаг 3. Рассчитывается оценка однородности. если если попадает в промежуток ( 0,1;0,2] то оценки плохо согласованы,
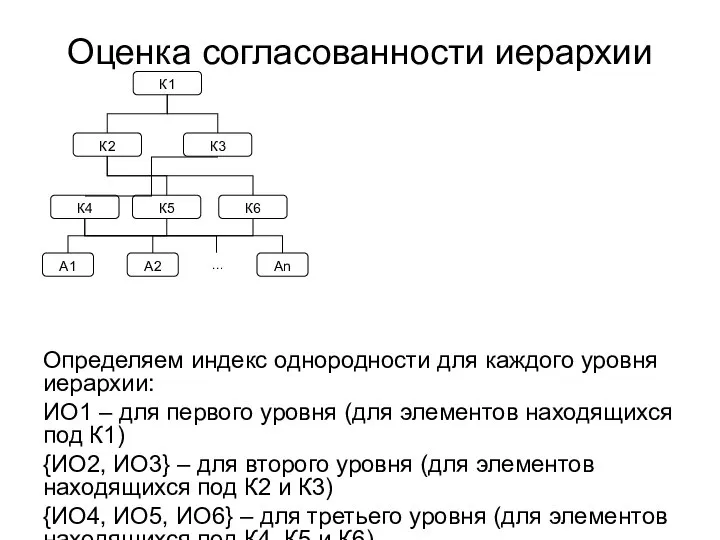
- 23. Оценка согласованности иерархии Определяем индекс однородности для каждого уровня иерархии: ИО1 – для первого уровня (для
- 24. W1, W2, W3 – векторы НЛП для элементов К1, К2 и К3. Однородность иерархии удовлетворительна для
- 26. Скачать презентацию










![Для получения нормированных приоритетов: , где [S] =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1161140/slide-17.jpg)



![Шаг 3. Рассчитывается оценка однородности. если если попадает в промежуток ( 0,1;0,2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1161140/slide-21.jpg)

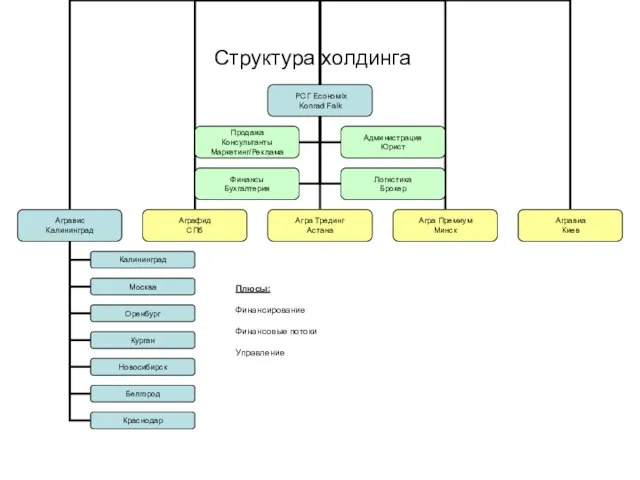 Структура холдинга
Структура холдинга Imagine – John Lennon
Imagine – John Lennon  Цели расследовательской деятельности журналиста
Цели расследовательской деятельности журналиста Синергетична концепція інноваційного розвитку інформаційного права
Синергетична концепція інноваційного розвитку інформаційного права Результаты исследования «SEO-альманах» ТопЭксперт.РФ
Результаты исследования «SEO-альманах» ТопЭксперт.РФ Профессиональная компетентность педагога
Профессиональная компетентность педагога Нормативно-правовые основы образования
Нормативно-правовые основы образования Задачи и объекты SWOT-анализа
Задачи и объекты SWOT-анализа Оформление и ведение учета операции с неплатежеспособными денежными знаками
Оформление и ведение учета операции с неплатежеспособными денежными знаками кибер-готы
кибер-готы Как увеличить вашу прибыль и расширить круг клиентов
Как увеличить вашу прибыль и расширить круг клиентов СOBIT® и ITIL®
СOBIT® и ITIL® Молодежный театр Эксперимент
Молодежный театр Эксперимент Компания «Винтер»
Компания «Винтер» Транспорт будущего
Транспорт будущего Анализ результатов Глобального опроса взрослого населения о потреблении табака в Российской Федерации и рекомендации для дальне
Анализ результатов Глобального опроса взрослого населения о потреблении табака в Российской Федерации и рекомендации для дальне himiki_i_ih_zaslugi
himiki_i_ih_zaslugi Кейс – технологии в учебном процессе
Кейс – технологии в учебном процессе Maslenitsa
Maslenitsa Ртуть
Ртуть Парные согласные в конце слова
Парные согласные в конце слова 10 вопросов о Солнце
10 вопросов о Солнце Дроби (6 класс)
Дроби (6 класс) Грибы
Грибы Мастер-классы по “Косметике для гурманов” учебного центра Yazykov-Group
Мастер-классы по “Косметике для гурманов” учебного центра Yazykov-Group Фонограф
Фонограф Организационное стимулирование
Организационное стимулирование Презентация на тему Internet-игра по русскому языку «Коротышкины задачи» с использованием web сервиса LearningApps.org
Презентация на тему Internet-игра по русскому языку «Коротышкины задачи» с использованием web сервиса LearningApps.org