Содержание
- 2. ТЕОРЕМА СИНУСОВ Стороны треугольника пропорциональны синусам противоположных углов
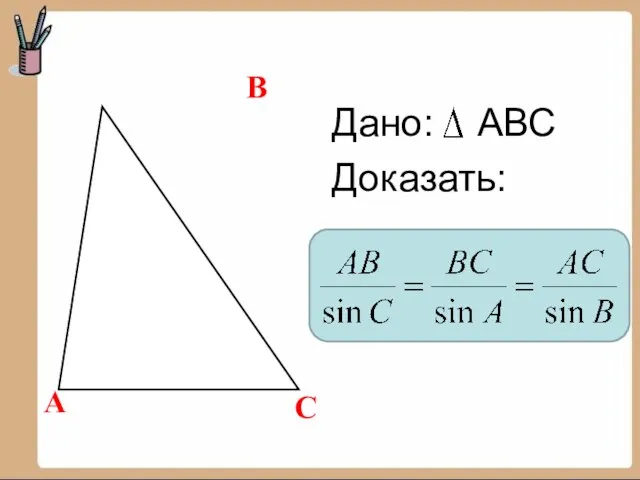
- 3. Дано: АВС Доказать: А В С
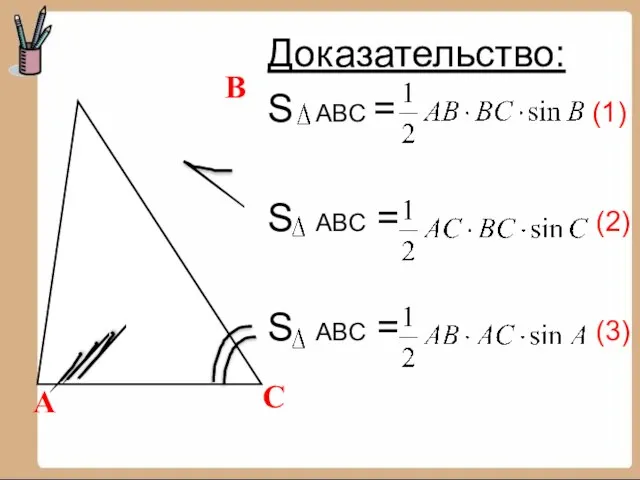
- 4. Доказательство: S ABC = (1) S ABC = (2) S ABC = (3) А В С
- 5. Приравняем равенства (1) и (2), получим = Сократим на , получим =
- 6. Приравняем равенства (2) и (3), получим = Сократим на , получим =
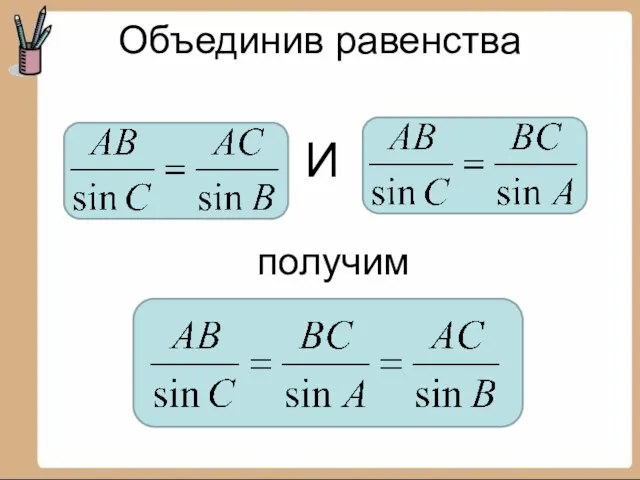
- 7. Объединив равенства И получим
- 8. Теорема косинусов Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон
- 9. Дано: АВС Доказать: a = b + c –2bc*cosA
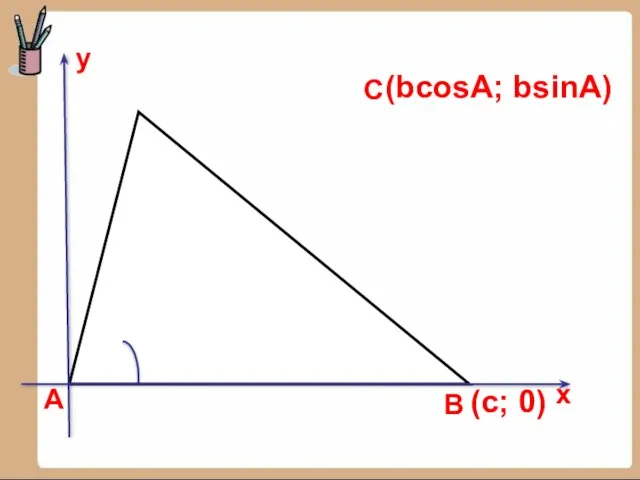
- 10. А С В (bcosA; bsinA) у х (с; 0)
- 11. Доказательство: Пусть в треугольнике АВС АВ = с, ВС = а, АС = b. Введем систему
- 13. Скачать презентацию






 Организация репликации Microsoft SQL Server 2000 с учётом внешних и внутренних ограничений системы
Организация репликации Microsoft SQL Server 2000 с учётом внешних и внутренних ограничений системы Результаты работы в группе /секции №4
Результаты работы в группе /секции №4 Жизнь и творчество Льва Николаевича Толстого
Жизнь и творчество Льва Николаевича Толстого Презентация на тему Подготовка к взрослости
Презентация на тему Подготовка к взрослости  Фотоальбом
Фотоальбом Штрих в рисунке
Штрих в рисунке Инновационные стратегии
Инновационные стратегии Австралия не разгаданная тайна земли
Австралия не разгаданная тайна земли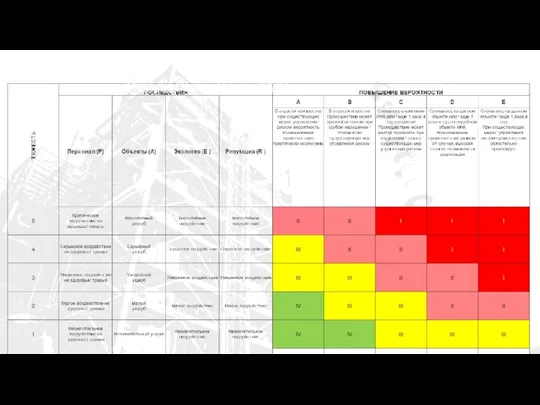 Матрица ОР
Матрица ОР Магистерская программа Бизнес и менеджмент (Business & Management)
Магистерская программа Бизнес и менеджмент (Business & Management) Призывнику
Призывнику БОРЬБА ЗА УДОВЛЕТВОРЕННОСТЬ КЛИЕНТОВ
БОРЬБА ЗА УДОВЛЕТВОРЕННОСТЬ КЛИЕНТОВ XIII Томский инновационный форум
XIII Томский инновационный форум Крещение (Богоявление)
Крещение (Богоявление) Образ Григория Мелехова
Образ Григория Мелехова Осторожно,железная дорога
Осторожно,железная дорога О С Т Е О П О Р О З
О С Т Е О П О Р О З Санкт-Петербургский государственный университетинформационных технологий, механики и оптики
Санкт-Петербургский государственный университетинформационных технологий, механики и оптики Развитие русской литературы 19 века
Развитие русской литературы 19 века Опорно-двигательный аппарат
Опорно-двигательный аппарат Аналитика: виды ROI
Аналитика: виды ROI Как формируются и утверждаются списки арбитражных заседателей. Тема 7. Вопрос 23
Как формируются и утверждаются списки арбитражных заседателей. Тема 7. Вопрос 23 Каменная архитектура
Каменная архитектура Физика и познание мира
Физика и познание мира Высокопроизводительные вычисления в системе управления жизненным циклом нефтегазовых месторождений
Высокопроизводительные вычисления в системе управления жизненным циклом нефтегазовых месторождений Аппаратные средства
Аппаратные средства Лукойл запускает проект Старт в будущее
Лукойл запускает проект Старт в будущее Конструкция: часть и целое здание как сочетание различных объемов
Конструкция: часть и целое здание как сочетание различных объемов