Основы экономико-математического моделирования

Основные положения теории моделирования.
Модель (с лат. «мера, мерило, образец») – некоторый образ объекта или системы объектов.
Модель- копия или аналог объекта-исследования, отображающая его существенные свойства.
Модель может быть определена как материально или мысленно представляемый объект, который отражает существенные свойства объекта – оригинала и замещает его в процессе исследования, т.о. изучение модели дает новые знания об объекте – оригинале, следовательно, модель является инструментом получения знаний об объекте – оригинале.
Моделирование – процесс исследование объекта, путем построения, изучения и применения моделей. Так как многие объекты невозможно исследовать непосредственно (объект недосягаем, исследование требует много времени и средств) необходимо использовать метод моделирования.
Все множество моделей по конструктивным особенностям делят на два класса: модели материальные, которые воплощены в материальных объектах; и модели идеальные, которые являются продуктом человеческого мышления.
В составе материальных (физических) моделей, в свою очередь, выделяют две подгруппы: модели геометрического подобия и модели–аналоги.
Модели геометрического подобия отражают структуру и геометрические характеристики оригинала, т.е. имеют одну и ту же физическую природу с аналогом (например, модель самолета в виде его уменьшенной копии).
Модели-аналоги отражают физические процессы, протекающие в аналоге, с помощью некоторых процессов, и могут иметь разную физическую природу по отношению к объекту-оригиналу (например, ЭВМ может рассматриваться в качестве модели деятельности человека по обработке информации).
Идеальные модели основываются на идеальной аналогии и делятся на знаковые и интуитивные.
Знаковые модели предполагают применение математического моделирования путем использования языка математики и логики (например, уравнения, алгоритмы решения задач, программы расчета на ЭВМ и т. д.)
В интуитивных моделях не используются знаковые системы, исследование основывается на интуиции. Эти модели встречаются в тех областях науки, где познавательный процесс находится на начальной стадии.

Процесс моделирования включает в себя три основных элемента: субъект (исследователь); объект исследования; модель, которая определяет отношения субъекта и объекта.
Сущность процесса моделирования отражают следующие этапы: построение модели, ее изучение, перенос знаний с модели на оригинал, а также практическая проверка полученных с помощью модели знаний и их использование для управления объектом.

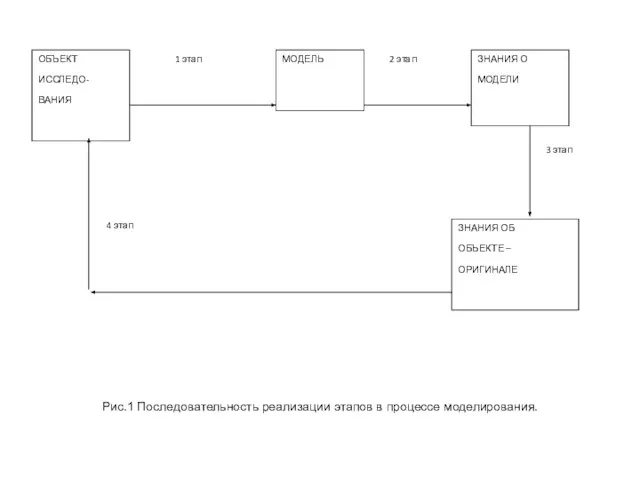
Рис.1 Последовательность реализации этапов в процессе моделирования.

Рассмотрим краткое содержание перечисленных этапов.
Первого этапа (построения модели) – предполагает наличие у исследователя некоторых знаний об объекте-оригинале (основные свойства, влияющие факторы, т.д.) При этом модель отображает существенные черты объекта оригинала.
На втором этапе (процесс изучения модели) модель выступает как самостоятельный объект исследования для проведения модельных экспериментов. В результате реализации второго этапа получаем совокупность знаний о модели.
На третьем этапе (переноса знаний с модели на оригинал) осуществляется формирование множества знаний об объекте-оригинале путем корректировки знаний о модели с учетом неучтенных ранее свойств оригинала.
На четвертом этапе, в результате практической проверки полученных с помощью модели знаний осуществляется построение обобщающей теории объекта с целью его преобразования и управления им.

2.Экономико-математические модели. Этапы и проблемы экономико-математического моделирования.
Экономико-математическая модель может быть определена как математическое описание социально-экономических систем, которое отражает их существенные свойства и замещает в процессе исследования.
Экономико-математическое моделирование представляет собой исследование социально-экономических систем при помощи экономико-математических моделей.
В экономических исследованиях используются преимущественно идеальные знаковые модели.
Материальные (физические) модели также могут применяться для исследования экономических систем. Однако возможности использования в экономике физического моделирования ограничены, что объясняется следующими причинами: во-первых, изучение отдельных частей народного хозяйства не дает полного представления об экономической системе в целом; во-вторых, трудно абстрагироваться от внешних воздействий на объект; в-третьих, проведение крупных реальных экспериментов требует больших затрат времени и средств, а также связанно с существенным риском. В целом в экономике физическое моделирование связано с понятием «экономического эксперимента».

Процесс экономико-математического моделирования носит циклический характер; в каждом цикле выделяются следующие этапы экономико-математического моделирования.
Первый этап экономико-математического моделирования – постановка экономической проблемы и ее качественный анализ. В ходе данного этапа выделяются важнейшие черты и свойства объекта исследования; производится анализ его структуры, взаимосвязи элементов; формулируется сущность проблемы и принимаемых допущений.
На втором этапе осуществляется построение математической модели в виде конкретной математической зависимости (уравнений, неравенств). В процессе формализации экономической проблемы целесообразно свести задачу к построению типовой модели, которая относится к хорошо изученному классу математических задач.
На третьем этапе – этапе математического анализа построенной модели – выявляются общие свойства модели и ее решений. При этом важным вопросом является доказательство существования решений в сформулированной модели: если математически задача не имеет решения, то следует скорректировать или постановку экономической задачи, или способы её математической формализации.
Четвертый этап экономико-математического моделирования – подготовка исходной информации; при этом используются методы теории вероятности и математической статистики для организации выборочных исследований, оценки достоверности данных. наиболее трудоемкий этап моделирования, при этом затраты на подготовку информации не должны превышать эффект от использования дополнительной информации
На пятом этапе осуществляется численное решение экономико-математической модели – включая разработку алгоритмов решения задачи, составление программ для ЭВМ и непосредственное проведение расчетов.
На завершающем – пятом этапе экономико-математического моделирования – проводятся анализ полученных результатов и их применение; при этом рассматривается правильность и полнота результатов моделирования, степень их практической применимости для решения поставленной на первом этапе проблемы.
Перечисленные этапы экономико-математического моделирования находятся в тесной взаимосвязи, возможны возвратные связи между этапами.

3. Классификация экономико-математических моделей.
В настоящее время не существует единой классификации экономико-математических моделей. Как правило, выделяют около десяти признаков классификации - рассмотрим важнейшие из них.
1. В зависимости от учета фактора времени выделяют экономико-математические модели статические и динамические.
Статические модели описывают свойства объекта по состоянию к определенному моменту (или определенному интервалу) времени. Динамические модели описывают экономическую систему в развитии.
2. По учету фактора неопределенности выделяют модели детерминированные и стохастические.
В детерминированных (детерминистических) моделях результаты на выходе однозначно определяются управляющими воздействиями без учета случайных факторов.
При задании на входе стохастической (вероятностной) модели определенной совокупности значений на её выходе могут быть получены разные результаты – в зависимости от действия случайного фактора. Модели этого типа сложнее детерминированных, однако более приближены к действительности.
3. В зависимости от цели создания и применения существуют модели оптимизационные, балансовые, трендовые и имитационные.
Оптимизационные модели предназначены для выбора наилучшего из определенного числа вариантов. Балансовые модели выражают требование соответствия наличия ресурсов и их использования. В трендовых моделях развитие моделируемой экономической системы отражается через тренд (длительную тенденцию) её основных показателей. И, наконец, имитационные модели предназначены для использования в процессе машинной имитации изучаемых систем или процессов