Системы счисления

СИСТЕМЫ СЧИСЛЕНИЯ
Система счисления (СС)- способ представления (записи) чисел с помощью некоторых символов (цифр)

ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ - 1
Единичная система – количество предметов изображалось нанесением черточек (засечек) на твердую поверхность (10-11 тыс. лет до н.э.)
Алфавитные системы (славянская, греческая, финикийская)– числа от 1 до 9 и целые количества десятков, сотен и т.д. обозначались символами

ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ - 2
«Особые числа»:
- 1 и 2 – первые числительные, остальные числа получались путем их повторения;
3,4 – числительные, связанные с окружающим миром и религией (3 царства, 4 стороны света);
5,10,20 – удобство использования для счета (число пальцев);
7 – число, связанное с небом (созвездие Б.Медведицы, лунная неделя, планеты-боги, радуга);
12 – «дюжина», для счета по пальцам (12 суставов) – время, знаки зодиака;
13 – «чертова дюжина», лишнее число
60 – время (минуты, секунды), углы
100 – «тьма»

ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ - 3
Первые цифры и запись чисел
Египетская - - Критская
Пример: 2367 =

ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ - 4
Римская система – значение числа равно:
1) сумме значений идущих подряд нескольких одинаковых «цифр» (группы первого вида);
2) разности значений двух «цифр», если слева от большей
«цифры» стоит меньшая. В этом случае от значения большей «цифры» отнимается значение меньшей «цифры». Вместе они образуют группу второго вида. Причем левая «цифра» может быть меньше правой максимум на один порядок: так перед L(50) и С(100) из «младших» может стоять только Х(10), перед D(500) и М(1000) -только С(100), перед V(5) — только 1(1);
3) сумме значений групп и «цифр», не вошедших в группы первого или второго вида.
Примеры: CDXLIV = (D - С) + (L - X) + (V - I) = 400 + 40 + 4
MCMLXXIV = М + (М - С) + L + (X + X) + (V - I) = 1000 + 900 + 50 + 20 + 4

ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ - 5
Мультипликативные системы – для записи одинакового числа единиц, десятков, сотен или тысяч применяются одни и те же символы, но после каждого символа пишется название сооветствующего разряда (Вавилон, племена Майя, Индия)
Пример: 323 схематично будет выглядеть так:
3Y 2Х 3
(где X – обозначение десятков, Y – обозначение сотен)

ИСТОРИЯ СИСТЕМ СЧИСЛЕНИЯ - 6
Десятичная система – возникла с введением нуля – «O» (от греческого Ouden – «ничто») (Индия, V век н.э.)

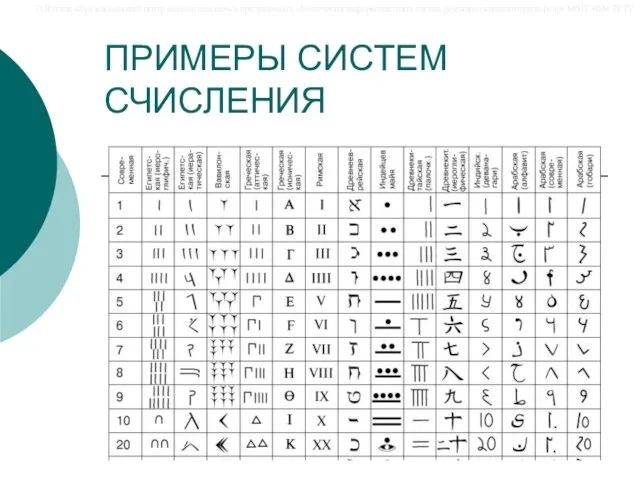
ПРИМЕРЫ СИСТЕМ СЧИСЛЕНИЯ

ПОЗИЦИОННЫЕ И НЕПОЗИЦИОННЫЕ СС
В непозиционных системах счисления вес цифры не зависит от позиции, которую она занимает в числе (XXXL)
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число (243, 324, 432)

ПОЗИЦИОННЫЕ СС
Количественное значение (величина) цифры определяется ее видом и положением в записи числа
Основание системы счисления – количество различных цифр, используемых для представления числа
Основание 10 у привычной десятичной системы счисления (десять пальцев на руках). Алфавит: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Основание 60 придумано в Древнем Вавилоне: деление часа на 60 минут, минуты — на 60 секунд, угла — на 360 градусов.
Основание 12 распространили англосаксы: в году 12 месяцев, в сутках два периода по 12 часов, в футе 12 дюймов.

ПРЕДСТАВЛЕНИЕ ЧИСЛА - 1
Позиция цифры в числе называется разрядом.
Aq = an-1×qn-1 + … + a1×q1 + a0×q0 + a-1×q-1 + … + a-m×q-m,
где
q — основание системы счисления (количество используемых цифр)
Aq — число в системе счисления с основанием q
a — цифры многоразрядного числа Aq
n (m) — количество целых (дробных) разрядов числа Aq
Пример:
2 1 0 -1 -2
239,4510 = 2×102 + 3×101 + 9×100 + 4×10-1 + 5×10-2.
a2 a1 a0, a-1 a-2

ПРЕДСТАВЛЕНИЕ ЧИСЛА - 2
Одно и то же число может быть представлено в различных системах счисления (с разными основаниями)
[47]
[.] – значение числа. Для простоты понимания значение числа всегда указывается в десятичной СС
1011112
12023
2234
578
4710
2F16

ПЕРЕВОД ЧИСЛА Np ⇒ Nq
Перевод числа из одной СС в другую осуществляется в два этапа:
переводится целая часть числа;
переводится дробная часть числа.

ПЕРЕВОД ЧИСЛА Np ⇒ Nq.
(правило перевода целой части числа)
Для перевода целого числа Np в число Nq необходимо Np делить на основание q (по правилам, принятым в ССp) до получения целого остатка, меньшего q. Полученное частное снова необходимо делить на основание q до получения целого остатка, меньшего q и т.д. до тех пор, пока последнее частное не будет меньше q.
Число Nq представится в виде упорядоченной последовательности цифр ССq (остатков от деления) в порядке, обратном получению, причем старшую цифру числа Nq даст последнее частное

ПЕРЕВОД ЧИСЛА Np ⇒ Nq.
(правило перевода дробной части числа)
Перевод правильной дроби Np в число Nq заключается в последовательном умножении дроби Np на основание q (по правилам, принятым в ССp), причем перемножению подвергается только дробная часть.
Дробь Nq представится в виде упорядоченной последовательности целых частей произведений в порядке их получения.
В общем случае при переводе может возникать погрешность вследствие конечности разрядной сетки. Если требуемая точность перевода есть q-k, то число указанных произведений должно быть равно k.

ПЕРЕВОД ЧИСЛА Np ⇒ Nq.
(упражнения)
34910 → ?4
0,4110 → ?2
24,1810 → ?3
53410 → ?16
...
3A16 → ?4
2,78 → ?10
3,78 → ?2
...

ПЕРЕВОД ЧИСЛА N8 ⇒ N2, N16 ⇒ N2
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему: каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
Примеры:
53718 = 101 011 111 0012;
5 3 7 1
1A3F16 = 1 1010 0011 11112
1 A 3 F

ПЕРЕВОД ЧИСЛА N2 ⇒ N8, N2 ⇒ N16
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
Примеры:
11010100001112 = 1 5 2 0 78;
1 101 010 000 111
1101110000011012 = 6 E 0 D16
110 1110 0000 1101

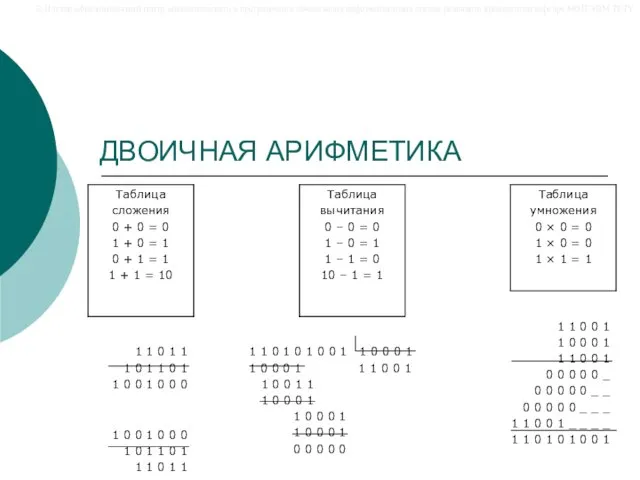
ДВОИЧНАЯ АРИФМЕТИКА

КОДЫ И КОДИРОВАНИЕ ЧИСЕЛ -1
Код – это правило, описывающее отображение одного набора знаков в другой набор знаков.
Кодом также называют множество образов, получаемых при этом отображении.
Примеры:
[45] = 1011012 (двоичное кодирование и двоичный код)
«A», «B», «1», «a», «+»,... = 65, 66, 49, 97, 43,..
(ASCII-код)

КОДЫ И КОДИРОВАНИЕ ЧИСЕЛ -2
Примеры кодов:
код Бэкона (1561-1626) – каждый символ представляется комбинацией из пяти символов «А» и «В»:
a = AAAAA, k = ABAAB, t = BAABA
код Грея – соседние слова отличаются не более, чем в одном разряде:

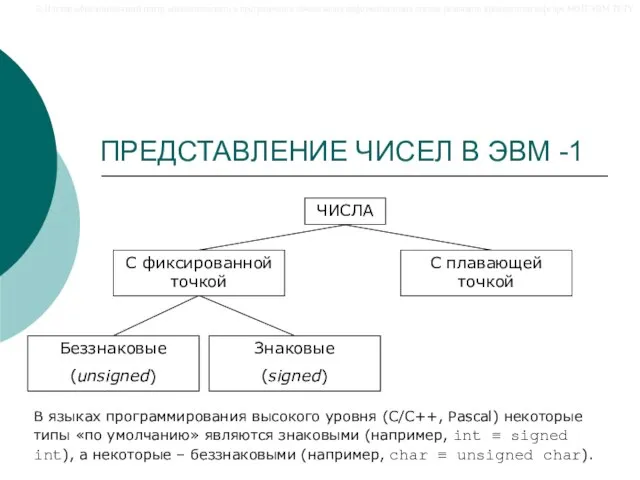
ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В ЭВМ -1
ЧИСЛА
С фиксированной точкой
С плавающей точкой
Беззнаковые
(unsigned)
Знаковые
(signed)
В языках программирования высокого уровня (С/С++, Pascal) некоторые типы «по умолчанию» являются знаковыми (например, int ≡ signed int), а некоторые – беззнаковыми (например, char ≡ unsigned char).

ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В ЭВМ -2
Достоинства: большой диапазон обрабатываемых значений
Недостатки: сложность в реализации устройства обработки
Числа с плавающей точкой:
при выполнении операций местоположение точки в записи
числа изменяется таким образом, чтобы слева от точки
оставался один разряд, а смещение точки описывалось
экспонентой:

ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В ЭВМ -3
Достоинства: простота реализации устройства обработки, высокая точность, интуитивная понятность
Недостатки: малый диапазон возможных значений
Числа с фиксированной точкой: местоположение точки в записи числа не изменяется.
Точка, разделяющая целую и дробную часть,
теоретически может располагаться между любыми двумя
разрядами.
На практике для целых ФЗ-чисел считается, что точка
расположена слева от самого младшего разряда:
01011001.

ПРЕДСТАВЛЕНИЕ ЧИСЕЛ БЕЗ ЗНАКА
Представление беззнакового (unsigned) числа соответствует его записи в заданной системе счисления (обычно двоичной или шестнадцатеричной)
Машинное представление числа (беззнакового или знакового) выполняется с учетом разрядности n машинного слова
Диапазон представления беззнаковых чисел:
0 ≤ x ≤ 2n-1

ПРЕДСТАВЛЕНИЕ ЧИСЕЛ СО ЗНАКОМ
Знаковые (signed) числа представляются в ЭВМ:
в прямом коде;
в обратном коде;
в дополнительном коде
Для обозначения знака числа в этих кодах выделяется специальный знаковый разряд, в котором записывается «0» для положительного числа и «1» для отрицательного числа.
Знаковый разряд всегда располагается слева от цифровых разрядов.

ПРЯМОЙ КОД
Число представляется в виде его абсолютного значения и кода знака
Диапазон представления:
1-2n-1 ≤ x ≤ 2n-1 - 1
Представления «0»:
[+0]пр = 0’00...02
[-0]пр = 1’00...02

ПРЯМОЙ КОД
(пример)
Представить в прямом коде для n=5, n=8
x = [13] x = [-13]
/x/ = /13/10 = 11012 = D16

ОБРАТНЫЙ КОД
Обратный код положительного числа x≥0 содержит «0» в старшем знаковом разряде и обычное представление x в остальных разрядах.
Если x≤0, то знаковый разряд содержит «1», а остальные разряды содержат инвертированные значения
Диапазон представления:
1-2n-1 ≤ x ≤ 2n-1 - 1
Представления «0»:
[+0]обр = 0’00...02
[-0]обр = 1’11...12

ОБРАТНЫЙ КОД
(пример)
Представить в обратном коде для n=5, n=8
x = [13] x = [-13]
/x/ = /13/10 = 11012 = D16

ПРАВИЛО СЛОЖЕНИЯ В ОБРАТНОМ КОДЕ
Коды слагаемых суммируются, включая знаковый разряд, с циклическим (круговым) переносом.
Результат верен, если не произошло переполнение.
Переполнение происходит тогда, когда перенос в знаковый разряд (Cs) не равен переносу из знакового разряда (Cs+1)

ДОПОЛНИТЕЛЬНЫЙ КОД
Дополнительный код положительного числа x≥0 содержит «0» в старшем знаковом разряде и обычное представление x в остальных разрядах (совпадает с прямым и обратным).
Если x≤0, то знаковый разряд содержит «1», а остальные разряды содержат дополнение модуля исходного числа до 2n-1.
Диапазон представления:
-2n-1 ≤ x ≤ 2n-1 - 1
Представление «0»:
[0]обр = 0’00...02

ДОПОЛНИТЕЛЬНЫЙ КОД
(пример)
Представить в дополнительном коде для n=5, n=8
x = [13] x = [-13]
/x/ = /13/10 = 11012 = D16

ПРАВИЛО СЛОЖЕНИЯ В ДОПОЛНИТЕЛЬНОМ КОДЕ
Коды слагаемых суммируются, включая знаковый разряд. Перенос (если он есть) отбрасывается.
Результат верен, если не произошло переполнение.
Переполнение происходит тогда, когда перенос в знаковый разряд (Cs) не равен переносу из знакового разряда (Cs+1)

УВЕЛИЧЕНИЕ РАЗРЯДНОСТИ ЧИСЕЛ ПРИ ПРИСВАИВАНИИ
Для беззнаковых (unsigned) чисел поле расширения в переменной-результате заполняется нулями
Для знаковых (signed) чисел поле расширения в переменной-результате заполняется знаковым битом
В языках высокого уровня способ расширения выбирается и реализуется компилятором по типу данных автоматически
В Ассемблере программист самостоятельно выбирает способ реализации расширения разрядности переменной

УМНОЖЕНИЕ ЦЕЛОГО ЧИСЛА НА КОНСТАНТУ ПОСРЕДСТВОМ СДВИГОВ
Сдвиг беззнаковых (unsigned) или знаковых (signed) числа влево на n двоичных разрядов приводит к его умножению на 2n
Если переменную V необходимо умножить на константу C, то константа C представляется в виде суммы степеней числа 2, а результат умножения записывается как сумма сдвигов числа V на показатели степеней.
V = V * 25;
Пример:
С = 25 = 110012 = 16+8+1 = 24 + 23 + 20
V = V*(16+8+1) = V*16 + V*8 + V = (V<<4) + (V<<3) + V
Достоинства: сдвиги и сложения выполняются быстрее, чем умножение
Недостатки: формула зависит от конкретного значения C, т.е. нельзя таким способом перемножить две переменных.