Содержание
- 2. История развития понятия функции Функция - одно из основных математических и общенаучных понятий. Оно сыграло и
- 3. Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых математически выраженных соотношениях между
- 4. Понятие переменной величины Греки рассматривали лишь вопросы, имеющие “геометрическую” природу, и не ставили вопроса об общем
- 5. Развитие механики и техники Развитие механики и техники потребовало введения общего понятия функции, что было сделано
- 6. Само слово “функция” (от латинского functio - совершение, выполнение) впервые было употреблено Лейбницем в 1673г. в
- 7. В 18 веке появляется новый взгляд на функцию как на формулу, связывающую одну переменную с другой.
- 8. Развитие понятия функции Следующий шаг в развитии понятия функции сделал гениальный ученик Бернулли, член Петербургской Академии
- 9. В общем виде понятие обобщенной функции было введено французом Лораном Шварцем. В 1936 году, 28-летний советский
- 10. Функцией называется соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент другого
- 11. Функции рядом с нами
- 12. Функции рядом с нами Любоваться природой можно и не зная математики. Но понять ее, увидеть то,
- 13. Знание законов природы дало человеку возможность объяснять и предсказывать ее разнообразнейшие явления. «Математическими портретами» закономерностей природы
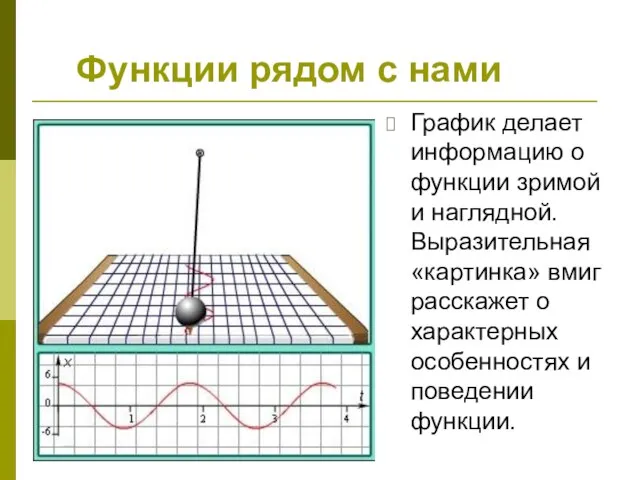
- 14. Функции рядом с нами График делает информацию о функции зримой и наглядной. Выразительная «картинка» вмиг расскажет
- 15. Функции рядом с нами «…Но кривая линия – геометрический эквивалент функции – гораздо больше говорит воображению,
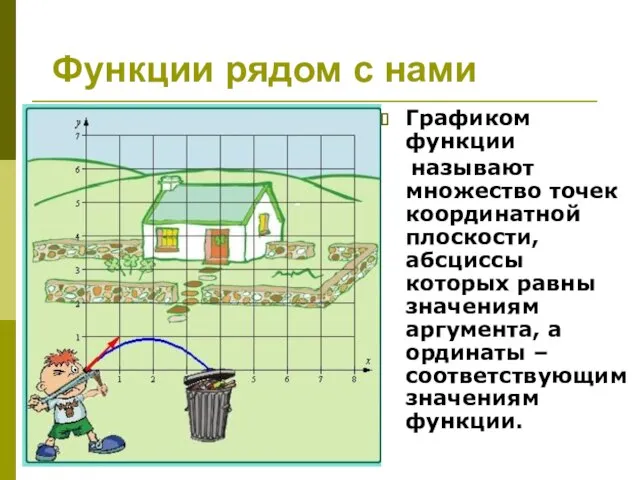
- 16. Функции рядом с нами Графиком функции называют множество точек координатной плоскости, абсциссы которых равны значениям аргумента,
- 17. Функции рядом с нами Чтобы наглядно проиллюстрировать характерные свойства функции, обратимся к пословицам. Ведь пословицы –
- 18. С помощью схематичных графиков функции проиллюстрируйте смысл пословиц: Каково жизнь проживёшь - такую славу наживёшь. Какой
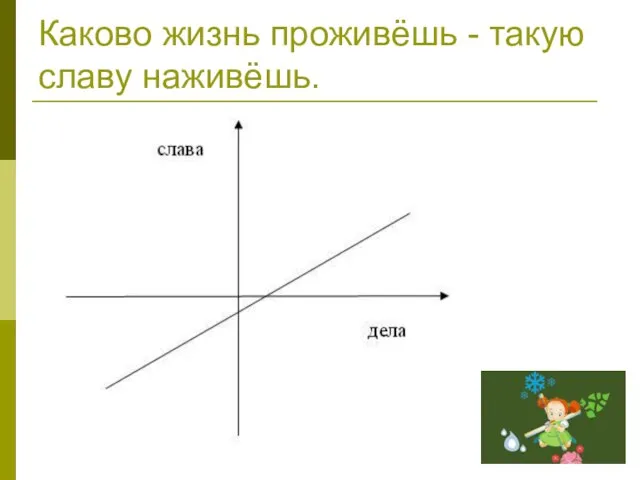
- 19. Каково жизнь проживёшь - такую славу наживёшь.
- 20. функции в нашей жизни
- 21. Диалектика природы «Когда математика стала изучать переменные величины и функции, лишь только она научилась описывать процессы,
- 22. Функции в нашей жизни Современная математика знает множество функций, и у каждой свой «неповторимый облик», как
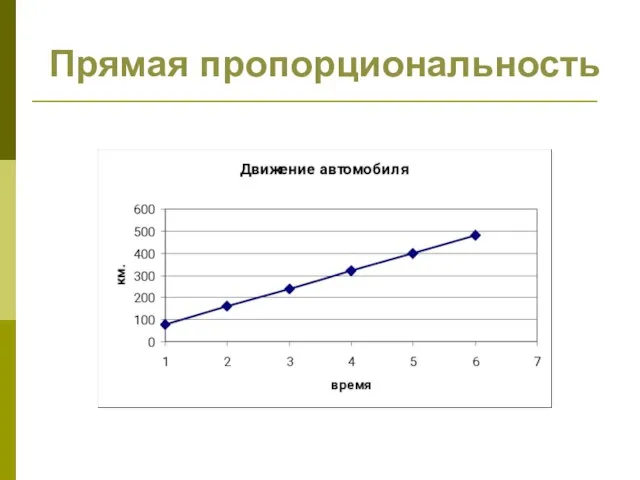
- 23. Прямая пропорциональность
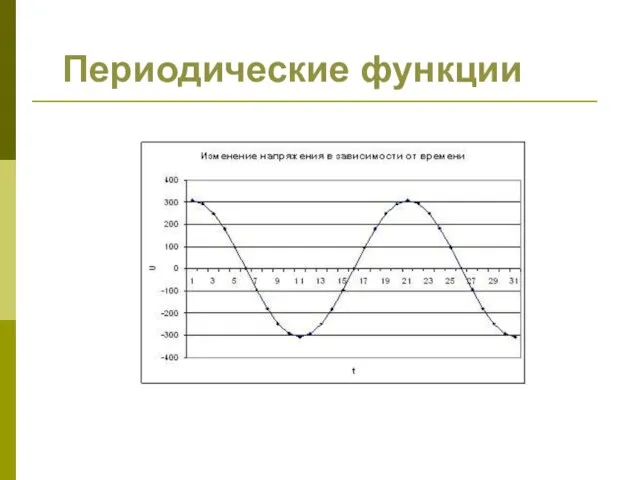
- 24. Периодические функции
- 25. Квадратичная функция Траекторией камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет
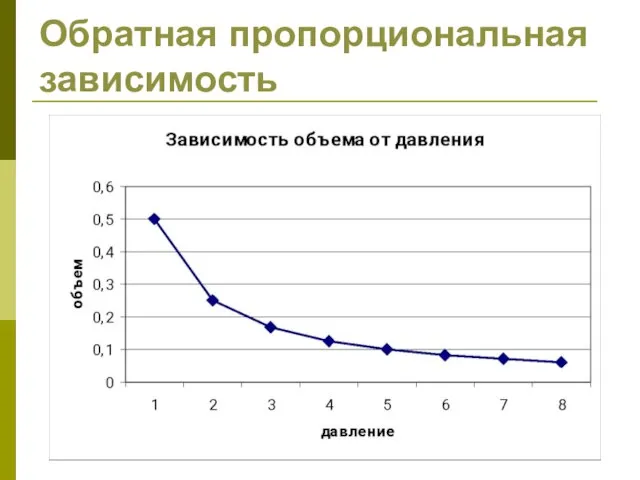
- 26. Обратная пропорциональная зависимость
- 27. Обратная пропорциональная зависимость
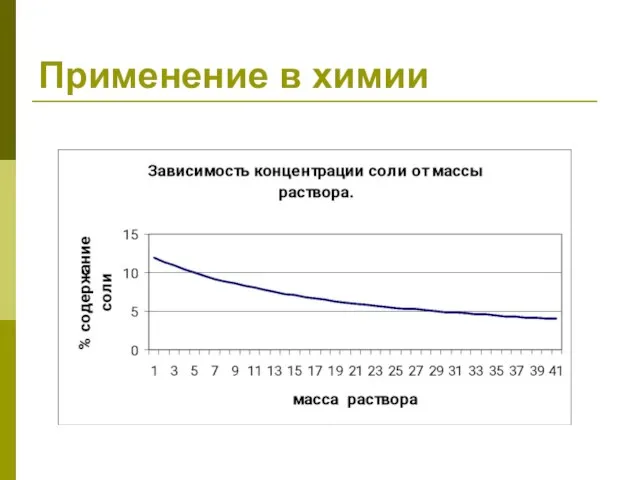
- 28. Применение в химии
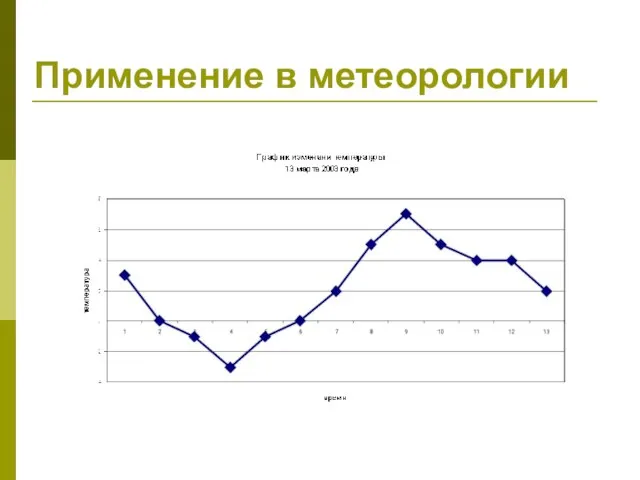
- 29. Применение в метеорологии
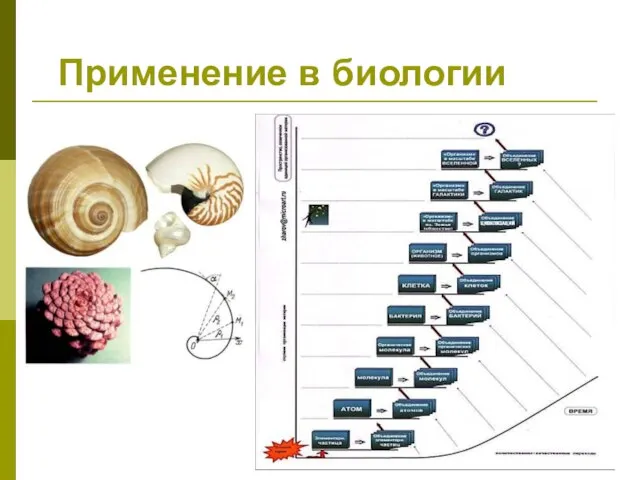
- 30. Применение в биологии
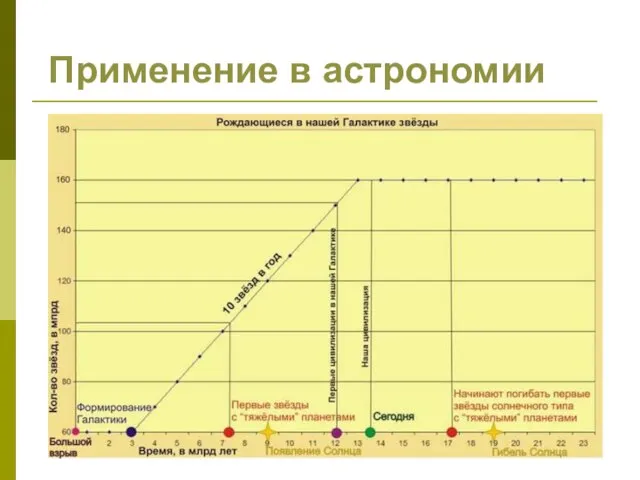
- 31. Применение в астрономии
- 32. Функции в нашей жизни В наши дни без функций невозможно не только рассчитать космические траектории, работу
- 34. Скачать презентацию


















 Почтовая открытка 23 февраля
Почтовая открытка 23 февраля Изомерия. Классификация органических веществ.
Изомерия. Классификация органических веществ. Обыкновенные дроби (5 класс)
Обыкновенные дроби (5 класс) Проектно- исследовательская деятельность младших школьников
Проектно- исследовательская деятельность младших школьников Стили речи. Введение в стилистику
Стили речи. Введение в стилистику Конкурс как способ организации досугового мероприятия
Конкурс как способ организации досугового мероприятия 1. Oppitunti (2)
1. Oppitunti (2) Разработка рекламных мероприятий по продвижению компании «Горячие туры» в социальных сетях Дипломный проект Рябиги О.С Группа Р
Разработка рекламных мероприятий по продвижению компании «Горячие туры» в социальных сетях Дипломный проект Рябиги О.С Группа Р 20141105_voronezh_segodnya
20141105_voronezh_segodnya Экосистема. Структура экосистемы
Экосистема. Структура экосистемы Славяне в древности
Славяне в древности 29.11.2011г.Студенты группы Ф -22 совместно с кураторомпосетили
29.11.2011г.Студенты группы Ф -22 совместно с кураторомпосетили Презентация 3
Презентация 3 9 «В» Февраль 2012
9 «В» Февраль 2012 дата проведения: 11.01.10Провела:Учитель информатики и ВТХрусцелевская Н.В.Прослушал:5 класс
дата проведения: 11.01.10Провела:Учитель информатики и ВТХрусцелевская Н.В.Прослушал:5 класс Тема: «Великий художник природы – вода».
Тема: «Великий художник природы – вода». Vox – Технология будущего
Vox – Технология будущего Architecture Styles in America
Architecture Styles in America  План проведения педагогического совета 1. Вступление. Анализ выполнения решений предыдущего педагогического совета. 2. Доклад «Сти
План проведения педагогического совета 1. Вступление. Анализ выполнения решений предыдущего педагогического совета. 2. Доклад «Сти Загадочная смерть Маяковского
Загадочная смерть Маяковского Учебное исследование и проектная работа. Основные понятия
Учебное исследование и проектная работа. Основные понятия ЯПОНИЯ
ЯПОНИЯ Характеристика и особенности оформления справок, докладных и объяснительных записок
Характеристика и особенности оформления справок, докладных и объяснительных записок Религиозная толерантность
Религиозная толерантность Презентация на тему Динамика материальной точки. Работа и энергия
Презентация на тему Динамика материальной точки. Работа и энергия
 IT Construct ООО «Ай Ти Констракт»
IT Construct ООО «Ай Ти Констракт» РАЗРАБОТКА И ВНЕДРЕНИЕ УЧЕБНИКОВ ПО БАЙКАЛОВЕДЕНИЮ В ШКОЛЬНОЕ ОБРАЗОВАНИЕ БАЙКАЛЬСКОГО РЕГИОНА
РАЗРАБОТКА И ВНЕДРЕНИЕ УЧЕБНИКОВ ПО БАЙКАЛОВЕДЕНИЮ В ШКОЛЬНОЕ ОБРАЗОВАНИЕ БАЙКАЛЬСКОГО РЕГИОНА Верховный суд США
Верховный суд США